Magnetic Field of a Solenoid Using Ampere's Law: Difference between revisions
No edit summary |
No edit summary |
||
| Line 15: | Line 15: | ||
== Example == | == Example == | ||
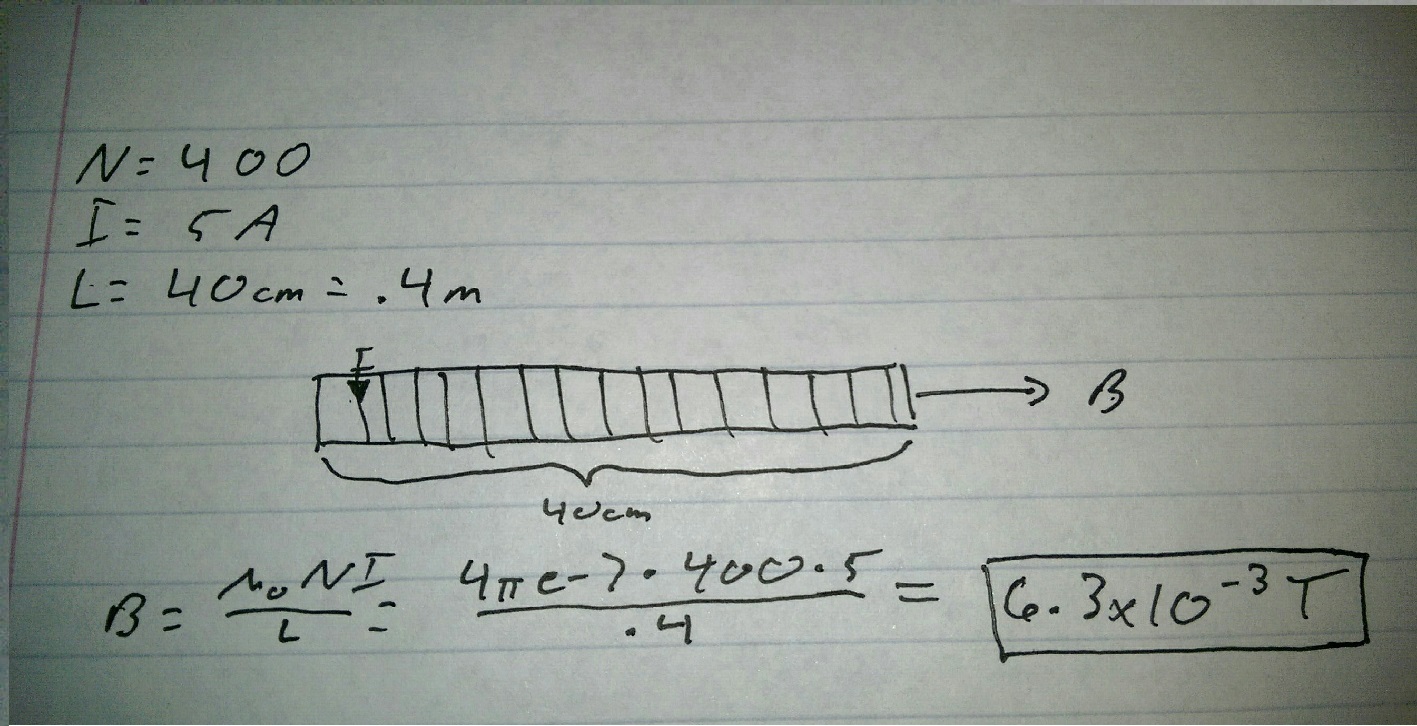
Find the magnetic field produced by the solenoid if the number of loops is 400 and current passing through on it is 5 A.( Length of the solenoid is 40cm) | Find the magnetic field produced by the solenoid if the number of loops is 400 and current passing through on it is 5 A.( Length of the solenoid is 40cm) | ||
[[File:Examplesolenoid.jpg]] | [[File:Examplesolenoid.jpg]] | ||
Revision as of 16:52, 13 April 2016
---- CLAIMED BY JAKE WEBB 3/8/16 ----
A solenoid is a long coil of wire with a very small diameter, often used to make electromagnets due to their ability to create strong magnetic fields. The magnetic field can be easily calculated along the axis of the solenoid using Ampere's Law, and the magnitude and direction of the field is constant throughout the entirety of the solenoid, excluding the ends.
Finding The Magnetic Field
If there are N loops of wire the compose a solenoid of length L, and we know that Ampere's Law for Magnetism gives us the form
∫B⋅dl = μ0∑I
This can be simplified to find that the magnitude if the magnetic field equals
B = μ0IN/L
The direction can be found using the Right Hand rule and will be along the axis of the solenoid.
Example
Find the magnetic field produced by the solenoid if the number of loops is 400 and current passing through on it is 5 A.( Length of the solenoid is 40cm)