Inelastic Collisions

This topic covers what inelastic collisions are, discusses a series of steps that can be undertaken to solve problems involving them, and then provides an example with the answers worked out. --Csorensen6 (talk) 21:06, 4 April 2016 (EDT)

The Main Idea

Inelastic collisions differ from elastic collisions in one primary aspect: the initial kinetic energy is not the same as the final kinetic energy. In other words, kinetic energy is NOT conserved, and Kf does not equal Ki. Momentum, however, is still conserved, so Pf = Pi. This is because, in all collisions, the forces involved in the collision are so large that external forces can be neglected. Consequently, given that ΔPsystem = Fnet,ext * ΔT, if we approximate Fnet,ext as zero, then ΔPsystem = 0.

Moreover, because the final kinetic energy differs from the initial kinetic energy, inelastic collisions witness a change in the internal energy of the objects involved in the collision. A change in internal energy often manifests itself in the objects deforming, rotating, getting hot, vibrating, exploding, or being excited to a higher energy state. In these collisions, the change in internal energy is equal to the negative change in kinetic energy, i.e. ΔEinternal = -ΔKtrans.

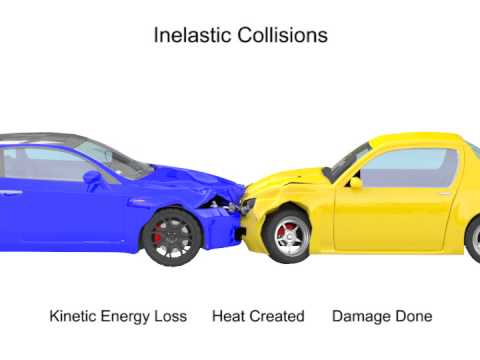
The picture below illustrates this.

Mathematical Model

In these types of problems, there are three main equations to consider:

ΔPsystem = Fnet,ext * ΔT = 0.

ΔE = ΔKtrans + ΔEinternal = 0

-ΔKtrans = ΔEinternal

Types of Inelastic Collisions

Maximally Inelastic Collisions

One of the most commonly-seen situations is the maximally inelastic collision, in which two objects collide and then stick together. The below image illustrates a maximally inelastic collision. More information about such problems can be found in the page about maximally inelastic collisions.

Explosions

In these types of problems, an object bursts apart, and some of its internal energy is converted into kinetic energy. As a result, ΔK is actually positive and ΔEint is actually negative, in that internal energy is used up in the course of the explosion and causes an increase in the speed of the particles involved. In other words, Ki < Kf.

Typical Inelastic Collisions

In these types, two or more objects collide but do not stick together, but as a result of their collision, one or both begins to rotate, begins to vibrate, deforms, gets hot, etc. In these problems, there is a positive ΔEint and a negative ΔK, and Ki > Kf. Most real-world collisions are inelastic like this, but to varying degrees.

Typical Process for Solving

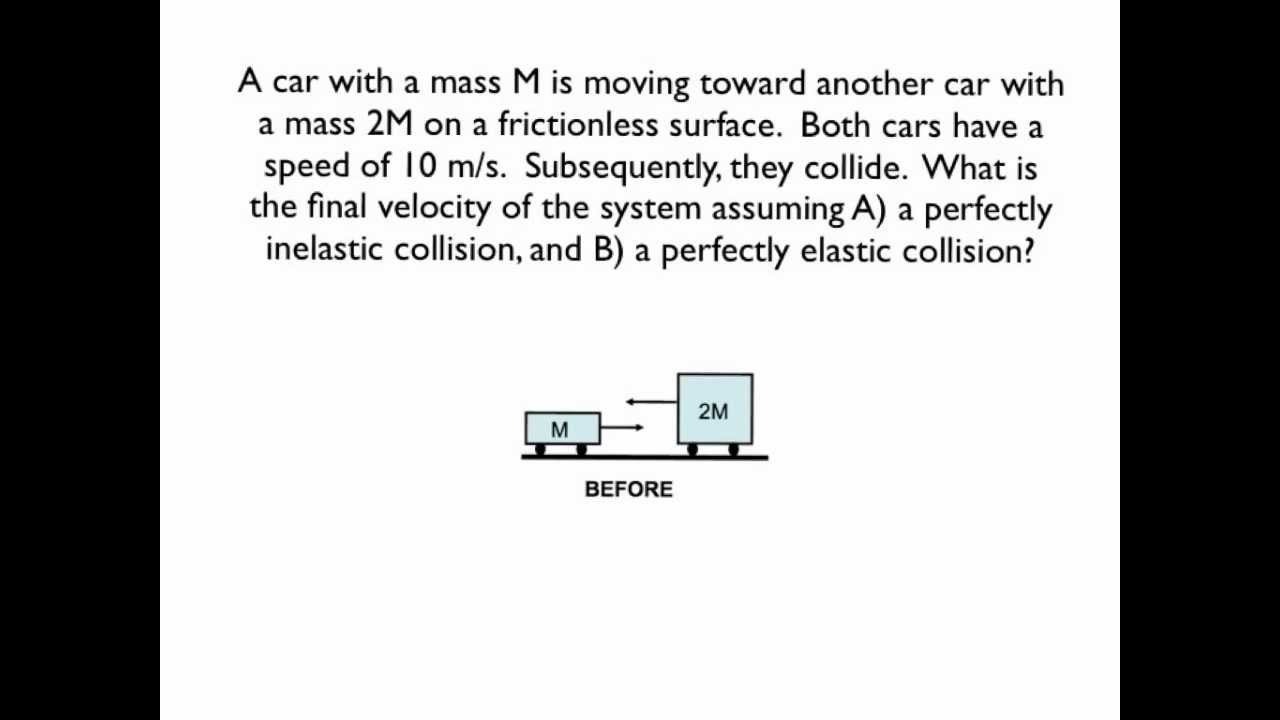
In such problems, it is often necessary to apply both the momentum principle and the energy principle. The image below provides an example of and the equations involved in solving a maximally inelastic collision problem.

The steps for solving inelastic collision problems are often as follows:

1) Draw a picture of the initial and final states.

2) Given that collisions involve extremely large forces acting over short time intervals, it is accurate to say that Fnet,ext = 0, because the external forces are typically much, much smaller than the internal forces involved in the collision.

3) Knowing that Fnet,ext = 0, this means that momentum is conserved and that Pf = Pi. This comes from the momentum principle, in that ΔP = Fnet,ext*ΔT, and if Fnet,ext is zero, then the right side of that equation is also zero.

4) Next, knowing that Pf = Pi, you can solve for any unknown velocities of the objects involved via the momentum principle.

5) Having determined the velocity of each object, you can then determine the initial and final kinetic energies of the system using K = (1/2)*m*|v|^2 for each object.

6) Next, you can find the change in kinetic energy, or ΔK, and this will be equal to the negative change in the internal energy (whether it be heat, rotation, etc.) gained by the objects in the course of the collision. In other words ΔEint = -ΔK.

Examples

Simple

Just do part A.

a)

  ΔP = Pf - Pi = Fnet,ext*ΔT = 0       
  Pi = Pf

  2M <-10,0,0> + M<10,0,0> = (2M + M)*vf
  <-10M,0,0> = 3M * vf

  vf = <-3.33, 0, 0> m/s

Middling

There are two hockey pucks traveling across the surface of a frozen pond. The first puck has a mass of 0.15 kg and is moving with a velocity of <2.5, 3.4, 0> m/s. The second puck has a mass of 0.13 kg and is moving with a velocity of <-3.1, 1.7, 0> m/s. After colliding, the first puck then has a velocity of <-1.9, 3.0, 0> m/s. (Reference the image below).

a) What is the velocity of the second puck after the collision?

b) What is the initial kinetic energy?

c) What is the final kinetic energy?

d) What is the change of the internal energy of the two pucks?

Answer

a)

  ΔP = Pf - Pi = Fnet,ext*ΔT = 0       
  Pi = Pf

  0.15kg<2.5, 3.4, 0> m/s + 0.13kg<-3.1, 1.7, 0> m/s = 0.15kg<-1.9, 3.0, 0> m/s + 0.13kg*v
  <-0.028, 0.731, 0> kg*m/s = <-0.285, 0.45, 0> kg*m/s + 0.13kg*v
  <0.257,0.281,0> kg*m/s = 0.13kg*v

  v = <1.977, 2.162, 0> m/s

b)

  K = (1/2)*m*|v|^2     
  |v| = (vx^2 + vy^2 + vz^2)^(1/2)      
  |v|^2 = vx^2 + vy^2 + vz^2
     
  Ki = (1/2)*0.15kg*((2.5 m/s)^2 + (3.4 m/s)^2 + (0 m/s)^2) + (1/2)*0.13kg*((-3.1 m/s)^2 + (1.7 m/s)^2 + (0 m/s)^2)
  Ki = 1.336 J + 0.813 J

  Ki = 2.149 J

c)

  K = (1/2)*m*|v|^2     
  |v| = (vx^2 + vy^2 + vz^2)^(1/2)      
  |v|^2 = vx^2 + vy^2 + vz^2   

  Kf = (1/2)*0.15kg*((-1.9 m/s)^2 + (3.0 m/s)^2 + (0 m/s)^2) + (1/2)*0.13kg*((1.977 m/s)^2 + (2.162 m/s)^2 + (0 m/s)^2)
  Kf = 0.946 J + 0.558 J

  Kf = 1.504 J

d)

  ΔE = Q + W = ΔK + ΔEinternal + ΔU + ΔErest
  ΔE = ΔK + ΔEinternal = 0 = Kf - Ki + ΔEinternal

  1.504 J - 2.149 J + ΔEinternal = 0
  -0.645J + ΔEinternal = 0

  ΔEinternal = 0.645 J

Difficult

A lit firework of mass 15 kg is launched into the sky with an initial velocity of <10,17,0> m/s. Eventually, its fuse burns up and the firework explodes, bursting into four parts. One piece has a mass of 3 kg and a velocity of <8,7,0> m/s. Another has a mass of 4 kg and a velocity of <15,0,0> m/s. The third has a mass of 3.5 kg and a velocity of <12,-5,0> m/s.

Reference the picture below.

a) What is the mass of the fourth piece?

b) What is the momentum of that piece?

c) What is the change in internal energy?

d) Justify the sign of the answer found in part c).

Answer

a)

b)

c)

d) The final kinetic energy is greater than the initial kinetic energy, and this is because, by exploding, some of the internal energy stored in the firework was released and then harnessed as kinetic energy.

  Consequently, the change in internal energy is negative.