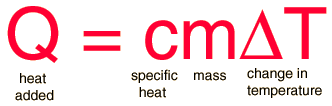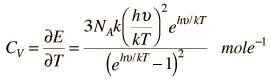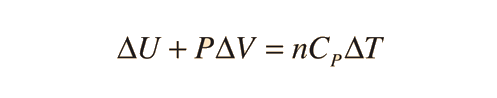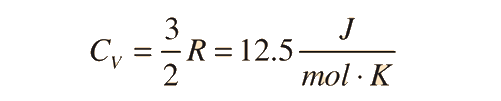Specific Heat

Specific Heat, also known as the specific heat capacity, is defined as the amount of heat required to raise the temperature of a unit mass by one degree Celsius. The units for specific heat are Joules per gram-degree Celsius (J / g °C).

The Main Idea

The most common definition is that specific heat is the amount of heat needed to raise the temperature of a mass by 1 degree. The relationship between heat and temperature change is best defined by constant "C" in the equation

To calcuate specfic heat, use the formula;

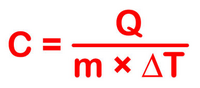
where the mass is in grams.

The relationship does not apply if a phase change is occurs because the heat added or removed during a phase change does not necessarily change the temperature. The specific heat most commonly known is the specific heat for water, which is 4.186 joule/gram °C or 1 calorie/gram °C. Water has a very large specific heat on a per-gram basis which means that it is very difficult to cause a change in its temperature. Since the specific heat of water is so high, water can be used for temperature regulation. Due to the difference in their atomic structures, the specific heat per gram for water is much higher than that for a metal. It is possible to predict the specific heat of an material, if you know about its atomic structure, as a rise in temperature is the increase in energy at the atomic level of substances. Generally, it is more more useful to compare specific heats on a molecular level.

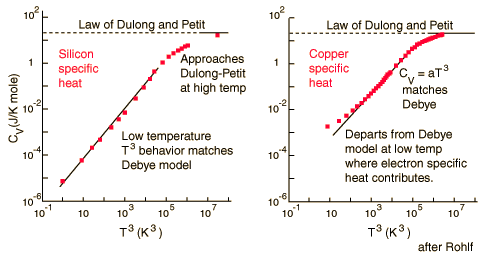
There are two ways to determine the specific heats of substances at the atomic level. These are the Dulong-Petit Law and the Einstein-Deybe model. The molar specific heats of most solids at room temperature are practically constant, which agrees with the Law of Dulong and Petit. At lower temperatures, the specific heats drop as atomic processes become more relevant. This behavior is explained by the Einstein-Debye model of specific heat.

Law of Dulong and Petit

[edit]

In 1819, French physicists, Pierre Louis Dulong and Alexis Thérèse Petit, discovered that the average molar specific heat for metals are approximately the same and equal to 25 J mole-1 oC-1 or roughly 3R where R is the gas constant for one mole. In this law, the amount of heat required to change the temperature is dependent on the number of molecules in the substance and not the mass.

ExampleThe specific heat of copper is 0.386 Joules/gram degrees Celsius while the specific heat of Aluminum is 0.900 Joules/gram Celsius. Why is there such a difference? Specific heat is measured in Energy per unit mass, but it should be measured in Energy per mole for more similar specific heats for solids. The similar molar specific heats for solid metals are what define the Law of Dulong and Petit.

The specific heats of metals, therefore should all be around 24.94 J/mol degrees Celsius. The specific heat at constant volume should be just the temperature derivative of that energy.

Copper 0.386 J/gm K x 63.6 gm/mol = 24.6 J/mol K

Aluminum 0.900 J/gm K x 26.98 gm/ mol = 24.3 J/mol K

Einstein Debye Model

[edit]

For low temperatures, Einstein and Debye found that the Law of Dulong and Petit was not applicable. At lower temperatures, it was found that atomic interactions were deemed significant in calculating the molar specific heat of an object.

According to the Einstein Debye Model for Copper and Aluminum, two solid metals, specific heat varies much at lower temperatures and goes much below the Dulong-Petit Model. This is due to increased effects on specific heat by interatomic forces. However, for very high temperature values, the Einstein-Debye Model cannot be used. In fact, at high temperatures, Einstein's expression of specific heat, reduces to the Dulong-Petit mathematical expression.

Here is the Einstein Debye Equation:

For high Temperatures it may be reduced like this:

This actually reduces to the Dulong-Petit Formula for Specific Heat:

Specific Heats of Gases

Specific heats of gases are generally expressed in their molar form due to the undefined volume or pressure of a gas. Usually only one is held constant. The first law of Thermodynamics helps to derive the formulas for specific heat for constant pressure and the specific heat for constant volume. Here is the equation:

There are two specific heats for gases, one for gases at a constant volume and one gases at a constant pressure. Since delta V is constant, or a constant volume the equation is:

For an ideal monatomic gas the molar specific heat should be around:

where Q is heat, n is number of moles, and delta T is change in Temperature.

For a constant pressure, specific heat can be derived as:

For and ideal monatomic gas, the molar specific heat should be around:

where Q is heat, n is number of moles, and delta T is change in Temperature.

The molar specific heats of gases all gravitate towards these ranges depending on the conditions the gas is kept in.

Connectedness

1. Specific heat can have a lot to do with prosthetic manufacturing, which is huge in Biomedical Engineering. Prosthetics materials must be durable and easy to manipulate in a normal range of temperatures. In order to created medical devices, specific heats must be known, especially for welding or molding things, which require a specific temperature to be effective. At higher temperatures, the Dulong-Petit law must be used to calculate the specific heat of an object. Especially for solid metal objects, which would be used in prosthetics, Dulong-Petit is especially useful.

See also

Heat Capacity

External links

[1]

References

This section contains the the references you used while writing this page:

http://hyperphysics.phy-astr.gsu.edu/hbase/emcon.html#emcon http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/spht.html http://scienceworld.wolfram.com/physics/SpecificHeat.html Matter & Interactions Vol I. Chabay Sherwood

Properties of Matter

Claimed by Felix Joseph

Main page Recent changes Random page Help

Tools

What links here Related changes Upload file Special pages Printable version Permanent link Page information

This page was last modified on 29 November 2015, at 23:04. This page has been accessed 525 times. Privacy policy About Physics Book Disclaimers