Superposition principle

Claimed by Abhinav Sundaresan: March 15, 2016

This topic covers the Superposition Principle. This was the first and original article on this topic (also the best).

The Main Idea

The superposition principle essentially states that in a given closed system, the 'reaction' of an object to outside forces is the sum of the outside force acting on it. These forces can act along multiple dimensions, therefore meaning that vector notation will be needed.

A Mathematical Model

The net electric field due to two or more charges is the vector sum of each field due to each individual charge. This not only applies to Electric Fields, but Magnetic Fields as well. It is important to note that in the superposition principle, the electric field caused by a charge is not affected by the presence of other charges.

[math]\displaystyle{ F(x_1+x_2)=F(x_1)+F(x_2) \, }[/math]

[math]\displaystyle{ F(a x)=a F(x) \, }[/math] 

A Computational Model

If [math]\displaystyle{ Q_1 }[/math] and [math]\displaystyle{ Q_2 }[/math] are positive and negative charges with charges of 6 nC and -5 nC respectively, what is the net electric field at point A located at (0,0,0)? Charge [math]\displaystyle{ Q_1 }[/math] is located at (2,-2,0). Charge [math]\displaystyle{ Q_2 }[/math] is located at (5,0,0). To begin this problem, the first step is to find [math]\displaystyle{ r_1 }[/math] [math]\displaystyle{ r_2 }[/math], the vectors from the charges to point A as well as their magnitudes:

[math]\displaystyle{ \vec{r_1} = 0\hat{i}+0\hat{j}-(2\hat{i}+-2\hat{j})\Rightarrow\vec{r_1} = -2\hat{i}+2\hat{j} }[/math]

[math]\displaystyle{ ||\vec{r_1}|| = \sqrt{2^2 + 2^2} =\sqrt{8} }[/math]

[math]\displaystyle{ \vec{r_2} = 0\hat{i}+0\hat{j}-(5\hat{i}+0\hat{j})\Rightarrow\vec{r_2} = -2\hat{i}+0\hat{j} }[/math]

[math]\displaystyle{ ||\vec{r_2}|| = \sqrt{-5^2 + 0^2} =\sqrt{25} }[/math]

Using Coloumb's Law, you get:

[math]\displaystyle{ \vec{E_1} = \frac{1}{4 \pi \epsilon_0}\frac{Q_1}{||r_1||^2}\hat{r_1}=\frac{1}{4 \pi \epsilon_0}\frac{e}{8}\lt \frac{-2}{\sqrt{8}}\hat{i}+\frac{-2}{\sqrt{8}}\hat{j}\gt = \lt -4.77\hat{i}+4.77\hat{j}\gt }[/math]N/C

[math]\displaystyle{ \vec{E_2} = \frac{1}{4 \pi \epsilon_0}\frac{Q_2}{||r_2||^2}\hat{r_2}=\frac{1}{4 \pi \epsilon_0}\frac{e}{5}\lt \frac{-5}{\sqrt{25}}\hat{i}+\frac{0}{\sqrt{25}}\hat{j}\gt = \lt 1.8\hat{i}+0\hat{j}\gt }[/math]N/C

Next, you need to add the two electric fields together. Because of the superposition principle, the electric field caused by Q1, does not effect the electric field created by Q2, but both can be summed together to create the net electric field at point A.

[math]\displaystyle{ \vec{E}=\vec{E_1}+\vec{E_2} = \lt -2.97\hat{i}+0\hat{j}\gt }[/math]

VPython Example

Here is a python program that calculates and displays the electric as well as magnetic field at a specific observation location for a moving dipole. The dipole is a negative and positive charge q and distance s. Write a porgram that will use the given constants to do this.

   # GlowScript 2.0 VPython
   
   magconstant = 1e-7
   oofpez = 9e9
   q=1.6e-19
   s = 1e-9
   pluscharge = sphere(pos=vector(-5*s, 0,-s/2), radius=1e-10, color=color.red)
   minuscharge = sphere(pos=vector(-5*s, 0, s/2), radius=1e-10, color=color.blue)
   velocity = vector(4e4,0,0) # The dipoles cm velocity    # The dipoles cm velocity
   robs = vector(0,s,0)
   
   # Initializes two arrows (E and B) at the observation location
   E = arrow(pos = robs, axis=vector(0,0,0), color = color.cyan)
   B = arrow(pos = robs, axis=vector(0,0,0), color = color.magenta)
   
   # Loop that updates dipole position as well as electric and magnetic field
   dt = 1e-18
   
   while pluscharge.pos.x < 10*s:
   
       rate(100)
       
       rplus = robs - pluscharge.pos
       rplusmag = mag(rplus)
       rplushat = norm(rplus)
       
       Eplus = ((oofpez * q) / (rplusmag ** 2))
       Bplus = magconstant * q * cross(velocity, rplushat) / rplusmag ** 2
       
       rminus = robs - minuscharge.pos
       rminusmag = mag(rminus)
       rminushat = norm(rminus)
       
       Eminus = (oofpez * (-q) / (rminus ** 2)) * rminus
       Bminus = (magconstant * (-q) * cross(velocity, rminushat)) / (rminushat ** 2)
       
       #Calculates the new E and B net fields
       Enet = Eplus + Eminus
       Bnet = Bplus + Bminus
       
       # Updates the E and B fields arrows
       E.axis = Enet
       B.axis = Bnet
       from visual import * #import the visual module
       
       rod = cylinder(pos=(0,2,1), axis=(5,0,0), radius=1)

Notice that this uses the principle of superposition. The magnetic and electric fields of the two particles in the dipole are added. This determines the net field at the observation location and is therefore a perfect example of superposition.

Examples

• 

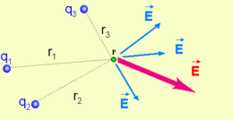
  This picture shows the electric field at the location of q3. Note that the Electric Fields of both q1 and q2 were both calculated individually (but do not react because of one another) and summed up to get the net electric field

• 

  Even by adding more source charges, the individual electric fields created by each source charge are unaffected by subsequent charges.

Connectedness

How is this topic connected to something that you are interested in?

• The Superposition Principle is important because it makes your life easier in Physics. You can make assumptions based on the fact that the net field at any location is equal to the sum of all the invidiual fields. You don't know one of the individual fields, but know the net field? Simple subtraction can help you calculate each individual field. Imagine if all Electric Fields influenced each other? It'd be really difficult to calculate net electric fields without a complicated equation that takes into account one field as a function of another. yuck. Thank the Physics Gods for the Superposition Principle.

How is it connected to your major?

• Since the Superposition Principle can be applied to circuits, and since Biomedical Engineering sometimes create medical device that require circuity, knowing how to create a circuit and calculate the electric field with the superposition principle is an important tool to have.

Is there an interesting industrial application?

• In this study, the Superposition Principle was used to analyze Solar Cells.

History

Daniel Bernouilli, in 1753, first proposed the idea of the Superposition Principle. He stated that "The general motion of a vibrating system is given by a superposition of its proper vibrations." His claim was rejected by mathematicians Leonhard Euler, and Joseph Lagrange. However they were eventually proved wrong by Joseph Fourier and it is now the concept you see today.

See also

• Coulomb's Law
• Electric Field
• Electric Dipole
• Electric Force
• Magnetic Force
• Magnetic Field

Further reading

• Additional Textbook Explanation

• Sparknotes Explanation

• This guy who made a Superposition principle on this wiki even though I already made one

External links

Instructional video on how to calculate the net electric field using the superposition principle

References

Chabay, Ruth W.; Sherwood, Bruce A. (2014-12-23). Matter and Interactions, 4th Edition: 1-2 (Page 522). Wiley. Kindle Edition.

Fields