Gravitational Force: Difference between revisions

Revision as of 11:17, 17 April 2016

CLAIMED BY BRIAN DUFFY This topic covers Newton's Law of Universal Gravitation.

Created by Ankit Khanal.

Main Idea

Gravitational Force, defined in Newton's law of Universal Gravitation is the attractive force between any two bodies of any mass, at any distance. Gravity is one of the essential forces that hold the Universe together. The law states that every object in the universe is exerting a pulling force on each other that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. Gravitational Force is considered to be the weakest of the four fundamental forces of nature: strong nuclear force, electromagnetic force, weak nuclear force and finally gravity. The first test of this law was performed in the laboratory by the British scientist Henry Cavendish in 1798, 72 years after the death of Sir Isaac Newton.

A Mathematical Model

The gravitational law states that every mass attracts any other mass by a force acting on the line intersecting both points. The force is directly proportional to the product of the masses and inversely proportional to the square distance between them. The two masses involved are assumed to be of uniform size, and considered point masses.

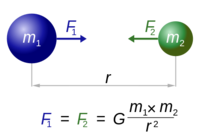
Two masses at a certain distance attracting each other

[math]\displaystyle{ |\vec{\mathbf{F}}_{grav}|= G \frac{m_1 m_2}{r^2}\ }[/math]

where,

F is the gravitational force between the masses;
G is the gravitational constant [math]\displaystyle{ 6.674×10^{−11} \frac{N m^2}{kg^2}\ }[/math];
m₁ is the mass of the first object;
m₂ is the mass of the second object;
r is the distance between the centers of both masses.

Vector Form

Newton's law of universal gravitation can be expressed in vector form to account for the direction of the gravitational force.

[math]\displaystyle{ \vec{\mathbf{F}}_{grav}= -G \frac{m_1 m_2}{r^2}\ }[/math][math]\displaystyle{ \mathbf{\hat{r}} }[/math]

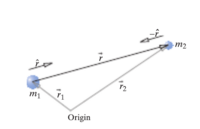
The relative position vector [math]\displaystyle{ \vec{\mathbf{r}} }[/math] is the distance from the center of object 1 to the center of object 2. The relative position between these two object can be represented as [math]\displaystyle{ \vec{\mathbf{r}}_{2-1} }[/math], which means that it is the difference between the position of object 1 and the position of object 2. The magnitude of [math]\displaystyle{ \vec{\mathbf{r}} }[/math], represented as [math]\displaystyle{ r^2 }[/math], is the distance between the center of two objects, found by taking the square root of the squares of each vector component. .

The direction of the gravitational force on object 2 by object 1 is specified by a unit vector,[math]\displaystyle{ -\mathbf{\hat{r}} }[/math], with a minus sign in front of it. The minus sign shows that the force on object 2 by 1 is in the opposite direction to [math]\displaystyle{ \mathbf{\hat{r}} }[/math].

Steps for calculating Gravitational Force

Calculate [math]\displaystyle{ \vec{\mathbf{r}} }[/math] by using the position of the center of object 2 relative to the center of object 1, keeping this in vector notation. i.e. [math]\displaystyle{ \vec{\mathbf{r}} = \vec{\mathbf{r}}_2-\vec{\mathbf{r}}_1 }[/math]
Calculate center to center distance between the objects, by finding the magnitude of the vector above [math]\displaystyle{ |\vec{\mathbf{r}}| }[/math]
Calculate [math]\displaystyle{ |\vec{\mathbf{F}}_{grav}| }[/math] using the equation for gravitational force
Calculate the unit vector [math]\displaystyle{ -\mathbf{\hat{r}} }[/math] =[math]\displaystyle{ \vec{\mathbf{r}} }[/math] /[math]\displaystyle{ |\vec{\mathbf{r}}| }[/math]
Multiply the Magnitude, [math]\displaystyle{ |\vec{\mathbf{F}}_{grav}| }[/math], by the unit vector.

Gravitational Force near the surface of the Earth is calculated by using:

[math]\displaystyle{ \vec{\mathbf{F}}_{grav} = mg }[/math]

where,

F is the force;
g is the magnitude of gravitational field near the Earth's surface;
m is the mass of the object.

This cannot be used for objects far from Earth or when determining the gravitational force from a different planet.

A Computational Model

A computational representation of Gravitational force can be created using VPython.

The code below show how we can find the net force, momentum and final position in Python.

while t < 235920:
      rate(5000)
      #Calculate the Gravitational Force acting on the craft due to Earth and Moon

Gravitational Interaction between the space craft, Earth and the Moon. The red arrow represents the momentum of the spacecraft at the moment

      #Craft to Earth Calculations
      r = craft.pos - Earth.pos
      rmag = sqrt(r.x**2 + r.y**2 + r.z**2)
      rhat = r / rmag
      fgravmag = -1 * ((G * mEarth * mcraft) / (rmag**2)) * rhat
      #Craft to Moon Calculations
      rmc = craft.pos - Moon.pos
      rmcmag = sqrt(rmc.x**2 + rmc.y**2 + rmc.z**2)
      rmchat = rmc / rmcmag
      fgravmoon = -1 * ((G * mMoon * mcraft) / (rmcmag**2))*rmchat      
      #Fnet is sum of these two forces
      fnet = fgrav + fgravmoon

From this we can calculate the change in momentum and the new positions using the net force.

      #Update the position of the spacecraft by calculating the new momentum and the new velocity
      pcraft = pcraft + (fnet*deltat)
      vcraft = pcraft / mcraft
      craft.pos = craft.pos + (vcraft*deltat)

Units

In Si Unit, Gravitational Force F is measured in Newtons (N), the two masses, m₁ and m₂ are measures in kilograms (Kg), the distance is measured in meters (m), and the gravitational constant G is measured in N m² kg^-2 and has a value of 6.674×10⁻¹¹ N m²kg⁻². The gravitation constant G is universal because no matter how big or small the masses are it is same for any interacting masses. The value of constant G appeared in Newton's law of universal gravitation, but it was not measured until seventy two years after Newton's death by Henry Cavendish with his Cavendish experiment in 1798. The value of gravitational constant was also the first test of Newton's law between two masses in Laboratory.

Examples

Problems taken from Textbook and old Test on T-square

Simple

Determine the force of gravitational attraction between the earth (m = [math]\displaystyle{ 6 x 10^{24} kg }[/math]) and a 70 kg physics student if the student is in an airplane at 40,000 feet above earth's surface. This would place the student a distance of [math]\displaystyle{ 6.38 x 10^6 m }[/math] from earth's center.

The solution of the problem involves substituting known values of G ([math]\displaystyle{ 6.673 x 10^{-11} }[/math] N m2/kg2), m₁ ([math]\displaystyle{ 6 x 10^{24} }[/math] kg), m₂ (70 kg) and d ([math]\displaystyle{ 6.38 x 10^6 m }[/math]) into the universal gravitation equation and solving for Fgrav. The solution is as follows:

[math]\displaystyle{ |\mathbf{F_{g}}| = G \frac{m_E m_M}{r^2} }[/math]

[math]\displaystyle{ |\mathbf{F_{g}}| = 6.7x10^{-11} \frac{6e24 * 70}{6.38 x 10^6} }[/math]

[math]\displaystyle{ |\mathbf{F_{g}}| =686 N }[/math]

Middling

The mass of the Earth is [math]\displaystyle{ 6 x 10^ {24} }[/math] kg, and the mass of the Moon is [math]\displaystyle{ 7 x 10^ {22} }[/math] kg. At a particular instance the moon is at location [math]\displaystyle{ \lt 2.8 x 10^8,0,-2.8 x 10^8\gt }[/math] m, in a coordinate system whose origin is at the center of the earth. (a) What is [math]\displaystyle{ \vec{\mathbf{r}} }[/math], the relative position vector from the Earth to the Moon? (b) What is [math]\displaystyle{ |\vec{\mathbf{r}}| }[/math]? (c) What is the unit vector [math]\displaystyle{ \vec{\mathbf{r}} }[/math]? (d) What is the gravitation force exerted by the Earth on the Moon? Your answer should be in vector.

The solution of the problem involves substituting known values of G ([math]\displaystyle{ 6.673 x 10^{-11} }[/math]N m²/kg²), m₁ [math]\displaystyle{ 6 x 10^ {24} }[/math] kg, m₂ [math]\displaystyle{ 7 x 10^ {22} }[/math] kg and d [math]\displaystyle{ \lt 2.8 x 10^8,0,-2.8 x 10^8\gt }[/math] m m into the universal gravitation equation and solving for F_grav. The solution is as follows:

Gravitational Force Between Moon and Earth

(a) The position vector of Moon relative to Earth is,

[math]\displaystyle{ \vec{\mathbf{r}} }[/math] = [math]\displaystyle{ \lt 2.8 x 10^8,0,-2.8 x 10^8\gt - \lt 0,0,0\gt }[/math]

[math]\displaystyle{ \vec{\mathbf{r}} }[/math] = [math]\displaystyle{ \lt 2.8 x 10^8,0,-2.8 x 10^8\gt }[/math] m

(b) The magnitude of position vector of Moon relative to Earth is,

[math]\displaystyle{ |\vec{\mathbf{r}}| }[/math] = [math]\displaystyle{ \sqrt{(2.8 x 10^8)^2+0^2+(-2.8 x 10^8)^2} }[/math]

[math]\displaystyle{ |\vec{\mathbf{r}}| }[/math] = [math]\displaystyle{ 4.0 x 10^8 }[/math] m

(c) The unit vector of Moon relative to Earth is,

[math]\displaystyle{ \mathbf{\hat{r}} = \frac {\vec{\mathbf{r}}}{|\vec{\mathbf{r}}|} }[/math]

[math]\displaystyle{ \mathbf{\hat{r}} = \frac{\lt 2.8 x 10^8,0,-2.8 x 10^8\gt }{4.0 x 10^8} }[/math]

[math]\displaystyle{ \mathbf{\hat{r}} = \lt 0.7,0,-0.7\gt }[/math]

(d) The expression for the gravitational force on the Moon by the Earth is,

[math]\displaystyle{ |\vec{\mathbf{F}}_{g}| = G \frac{m_E m_M}{|\vec{\mathbf{r^2}}|} }[/math]

[math]\displaystyle{ |\vec{\mathbf{F}}_{g}| = 6.7x10^{-11} \frac{6 x 10^ {24} * 7 x 10^ {22}}{(4.0 x 10^8)^2 } }[/math]

[math]\displaystyle{ |\vec{\mathbf{F}}_{g}| = 1.76x10^{20}N }[/math]

[math]\displaystyle{ \vec{\mathbf{F}}_{g} }[/math] = [math]\displaystyle{ -|\mathbf{F_{grav}}|*{\mathbf{\hat{r}}} }[/math]

[math]\displaystyle{ \vec{\mathbf{F}}_{g} }[/math] = [math]\displaystyle{ -1.76x10^{20}*\lt 0.7,0,-0.7\gt N }[/math]

[math]\displaystyle{ \vec{\mathbf{F}}_{g} }[/math] = [math]\displaystyle{ \lt -1.232x10^{20},0,1.232x10^{20}\gt N }[/math]

Difficult

In the following problems you will be asked to calculate the net gravitational force acting on the Moon.To do so, please use the following variables:

Mass

m_S - Mass of the Sun

m_E - Mass of the Earth

m_M - Mass of the Moon

Initial Positions

[math]\displaystyle{ \vec{\mathbf{r_{S}}} = \lt 0,0,0\gt m }[/math]- Position of the Sun

[math]\displaystyle{ \vec{\mathbf{r_{E}}} }[/math] = <[math]\displaystyle{ L,0,0\gt }[/math] m- Position of the Earth

[math]\displaystyle{ \vec{\mathbf{r_{M}}} }[/math] = <[math]\displaystyle{ L,h,0\gt }[/math] m - Position of the Moon

(a) Calculate the gravitational force on the Moon due to the Earth (b) Calculate the gravitational force on the Moon due to the Sun (c) Calculate the net gravitational force on the Moon

(a) The gravitational force on the Moon due to the Earth is,

[math]\displaystyle{ \vec{\mathbf{r}} = \vec{\mathbf{r_M}}-\vec{\mathbf{r_E}} }[/math]

[math]\displaystyle{ \vec{\mathbf{r}} }[/math] = <[math]\displaystyle{ L,h,0\gt }[/math]-<[math]\displaystyle{ L,0,0\gt }[/math]

[math]\displaystyle{ \vec{\mathbf{r}} }[/math] = <[math]\displaystyle{ 0,h,0\gt m }[/math]

[math]\displaystyle{ |\vec{\mathbf{r}}| = \sqrt{(0^2+h^2+0^2)} }[/math]

[math]\displaystyle{ |\vec{\mathbf{r}}| = h }[/math] m

[math]\displaystyle{ \mathbf{\hat{r}} = \frac {\vec{\mathbf{r}}}{|\vec{\mathbf{r}}|} }[/math]

[math]\displaystyle{ \mathbf{\hat{r}} = \frac{\lt 0,h,0\gt }{h} }[/math]

[math]\displaystyle{ \mathbf{\hat{r}} = \lt 0,1,0\gt }[/math]

[math]\displaystyle{ |\vec{\mathbf{F}}_{g_1}| = G \frac{m_E m_M}{|\vec{\mathbf{r^2}|}} }[/math]

[math]\displaystyle{ |\vec{\mathbf{F}}_{g_1}| = G \frac{m_E m_M}{h^2} }[/math]

[math]\displaystyle{ \vec{\mathbf{F}}_{g_1} = -|\vec{\mathbf{F}}_{g_1}|*{mathbf{\hat{r}}} }[/math]

[math]\displaystyle{ \vec{\mathbf{F}}_{g_1} = \lt 0,-G \frac{m_E m_M}{h^2},0\gt N }[/math]

(b) The gravitational force on the Moon due to the Sun is,

[math]\displaystyle{ \vec{\mathbf{r}} = \vec{\mathbf{r_M}}-\vec{\mathbf{r_S}} }[/math]

[math]\displaystyle{ \vec{\mathbf{r}} }[/math] = <[math]\displaystyle{ L,h,0\gt -\lt 0,0,0\gt }[/math]

[math]\displaystyle{ \vec{\mathbf{r}} }[/math] = <[math]\displaystyle{ L,h,0\gt m }[/math]

[math]\displaystyle{ |\vec{\mathbf{r}}| = \sqrt{(L^2+h^2+0^2)} }[/math]

[math]\displaystyle{ |\vec{\mathbf{r}}| = \sqrt{(L^2+h^2)} }[/math]

[math]\displaystyle{ \mathbf{\hat{r}} = \frac {\vec{\mathbf{r}}}{|\vec{\mathbf{r}}|} }[/math]

[math]\displaystyle{ \mathbf{\hat{r}} = \frac {\lt (L,h,0)\gt }{\sqrt{(L^2+h^2)}} }[/math]

[math]\displaystyle{ |\vec{\mathbf{F}}_{g_2}| = G \frac{m_S m_M}{|\vec{\mathbf{r^2}|}} }[/math]

[math]\displaystyle{ |\vec{\mathbf{F}}_{g_2}| = G \frac{m_S m_M}{L^2+h^2} }[/math]

[math]\displaystyle{ \vec{\mathbf{F}}_{g_2} = -|\vec{\mathbf{F}}_{g_2}|*{\mathbf{\hat{r}}} }[/math]

[math]\displaystyle{ \vec{\mathbf{F}}_{g_2} = \lt -G \frac{m_S m_M L}{(L^2+h^2)^{3/2}},-G \frac{m_S m_M h}{(L^2+h^2)^{3/2}},0\gt N }[/math]

(c) The net gravitational force on the Moon is,

[math]\displaystyle{ \vec{\mathbf{F}}_{net} = \vec{\mathbf{F}}_{g_1}+\vec{\mathbf{F}}_{g_2} }[/math]

[math]\displaystyle{ \vec{\mathbf{F}}_{net} = \lt 0,-G \frac{m_E m_M}{h^2},0\gt +\lt -G \frac{m_S m_M L}{(L^2+h^2)^{3/2}},-G \frac{m_S m_M h}{(L^2+h^2)^{3/2}},0\gt }[/math]

[math]\displaystyle{ \vec{\mathbf{F}}_{net} = \lt -G \frac{m_S m_M L}{(L^2+h^2)^{3/2}},-G \frac{m_E m_M}{h^2}-G \frac{m_S m_M h}{(L^2+h^2)^{3/2}},0\gt N }[/math]

Connectedness

The very first thing I remember learning in physics was gravity, how it worked and why it was so important. This is the reason why I am very interested in physical interactions. Newton's Law of Universal Gravitation is very important when it comes to describing and understanding the interactions between planets and there moons to how entire galaxies move.

This topic has nothing to do with my major.

Newton's Law of Universal Gravitation is related to every physical that we see around us. Every time you jump, we experience gravity. It pulls us back down to the ground. Without gravity, we'd float off into the atmosphere, along with all of the other matter on earth. It can be used to discover new planets, find the escape velocity needed to escape from any planet, and it can also used to launch satellites in the space and keep it spinning in an circular path. See to learn more about gravitational Force and its application.

History

Sir Isaac Newton, the 17^th century English scientist, is popularly associated with gravity but scientists had been studying gravity for centuries before Newton. Based on Galileo’s and Kepler’s works, Newton published “Principia” in 1687, in which he explained that the force that makes planets move around the Sun is the same force that makes objects fall in the Earth. Newton explained that gravity is a force that attracts different masses and is inversely proportional to the square distance between the objects. However Newtons did not fully understand how gravitational force acted from one object to another over vast distances. Despite this flaw, this law has been used for more than three centuries and is still used by scientists. Albert Einstein rejected in theory and explained it in his general theory of relativity, in which he stated that gravity is not a force but it is a consequence of the curvature of space-time. Even Einstein did not fully explain gravitational force.

2: Rankin, Alan. "What Is a Gravitational Force?" WiseGeek. Conjecture, n.d. Web. 28 Nov. 2015. <http://www.wisegeek.com/what-is-a-gravitational-force.htm>

3: "History of Gravity." History of Gravity. N.p., n.d. Web. 28 Nov. 2015. <https://www.physics.wisc.edu/museum/Exhibits-1/Mechanics/GravPit/index_HistGrav-2.html>

4: <https://en.wikipedia.org/wiki/Newton%27s_law_of_universal_gravitation>

5: <https://amabute.files.wordpress.com/2012/01/applenewton1.jpg>

Gravitational Force: Difference between revisions

Revision as of 11:17, 17 April 2016

Contents

Main Idea

A Mathematical Model

Vector Form

A Computational Model

Units

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu