RC Circuit

CLAIMED BY MARK RUSSELL SPRING 2016

The Main Idea

The figure below shows a capacitor, ( C ) in series with a resistor, ( R ) forming a RC Charging Circuit connected across a DC battery supply ( Vs ) via a mechanical switch. When the switch is closed, the capacitor will gradually charge up through the resistor until the voltage across it reaches the supply voltage of the battery. The manner in which the capacitor charges up is also shown below.

Let us assume left, that the capacitor, C is fully “discharged” and the switch (S) is fully open. These are the initial conditions of the circuit, then t = 0, i = 0 and q = 0. When the switch is closed the time begins at t = 0 and current begins to flow into the capacitor via the resistor.

Since the initial voltage across the capacitor is zero, ( Vc = 0 ) the capacitor appears to be a short circuit to the external circuit and the maximum current flows through the circuit restricted only by the resistor R.

As the capacitor charges up, the potential difference across its plates slowly increases with the actual time taken for the charge on the capacitor to reach its maximum possible voltage. The maximum voltage the capacitor reaches is equal to the voltage supply of the battery. Once the potential difference across the plates of the capacitor equals the battery's voltage supply, current will stop flowing through the circuit. This is known as the steady state of an RC circuit; it is reached when time goes to infinity.

A Mathematical Model

ΔV = I * R

Q=CV

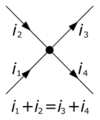
Node Rule-Current is assigned (positive or negative) quantity reflecting direction towards or away from a node. This principle can be solved by adding all the currents up to equal 0. The Node Rule is important to RC Circuits because finding the current flow in the different states of an RC Circuit often relies on nodes when the capacitor is in parallel.

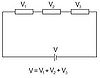
Loop Rule-Similar to the node rule; however, the voltage jumps and drops are added up around the circuit to equal to 0.

Examples

Simple

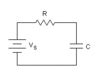
In the steady state what is the potential difference across the plates of the capacitor? The circuit has a resistor, R, capacitor, C, and battery, Vs.

Solution: The key concept in this problem is that in the steady state time is approaching infinity. In an RC circuit as time approaches infinity, the current is 0 because the potential difference across the capacitor equals that of the battery. Therefore, the potential difference across the plates of the capacitor equals Vs.

Difficult

The circuit below has been in position a for a long time. At time t = 0 the switch is thrown to position b. DATA: Vb = 12 V, C = 10 mF, R = 20 W

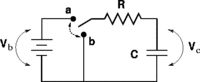
a.) What is the current through the resistor just BEFORE the switch is thrown?

The circuit is in a steady state so I = 0

b.) What is the current through the resistor just AFTER the switch is thrown?

Solution: I = V/R I = 0.6 amps since the capacitor has a potential difference and is creating the current.

c.) What is the charge across the capacitor just BEFORE the switch is thrown?

Solution: Q = CV Q = 120 mC

d.) What is the charge on the capacitor just AFTER the switch is thrown?

Solution: Charge does not change instantaneously Q = 120mC

Connectedness

1. How is this topic connected to something that you are interested in?

RC Circuits can be used in musical instruments such as guitars and amplifiers. I play the guitar so it is cool to see how the guitar actually works.

1. How is it connected to your major?

Mechanical Engineering requires the use of many electronics and learning how various circuits work is necessary for creating new parts and machines.

1. Is there an interesting industrial application?

RC circuits can be used in many industrial areas to allow certain frequencies to pass through a circuit.

See also

Further reading

Charge in a RC Circuit

Current in a RC circuit

Loop Rule

Node Rule

Current

External links

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/rcimp.html

http://www.allaboutcircuits.com/textbook/alternating-current/chpt-4/series-resistor-capacitor-circuits/

References

http://www.electronics-tutorials.ws/rc/rc_1.html

https://www.pa.msu.edu/courses/1997spring/PHY232/lectures/kirchoff/examples.html