SI units

This page is about SI Units. This page is created by Jinyoung Lee and edited by Brenda Dang.

The Main Idea

SI unit stands for the 'International System of Units'. It is the modern form of the metric system and is the most widely used system of measurement. It is made up of 7 base units and defined by twenty-two named units. However, it also includes many more unnamed coherent derived units. The system also establishes a set of twenty prefixes to the unit names and unit symbols that may be used when specifying multiples and fractions of the units. When created by Carl Friedrich Gauss in the 1830's, SI was intended to be an evolving system rather than a permanent solution. SI unit definitions are continuously modified through international agreement as the technology of measurement progresses and the precision of measurements improves.

The image above shows a few of the common derived SI units mentioned above. For more information, please see Derived SI Units below.

A Mathematical Model

There is some mathematical operation required to translate a non-SI unit to SI unit. For example, [math]\displaystyle{ {\frac{lb}{2.2}} = kg }[/math] Since 1 kg(SI unit) is equal to 2.2 lb, to change lb to SI unit, lb must be divided by 2.2.

Another example is length. [math]\displaystyle{ {\frac{inch}{0.394}} = cm }[/math] The same method used to change lb to kg. Since 1 cm is equal to 0.394 inch, inch has to be divided by 0.394 to become SI unit, cm.

Base SI units

This image above shows the base SI units. These units include length, mass, time, electric current, temperature, substance amount, and light intensity.

Prefix

Numbers in physics, such as mass or length, can be very small or very large. Electrons are a great example of this. The mass of an electron is 0.0000000000000000000000910938356g or 9.10938356 E-31. In SI, prefixes are available to adjust the size of a unit so as to keep the number of those units reasonable. In the example of electrons above, it is inconvenient to read the number aloud. However, using prefixes can simplify that process. The image below shows the list of prefixes in SI.

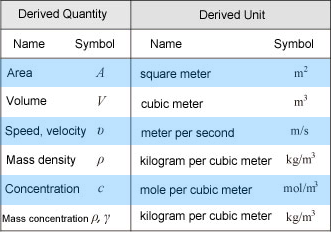
Derived SI units

This image above shows the relationships between many units used in physics based on base SI units. As we can see, most of the units in physics are related to the SI units. This is because there are many quantities that cannot be expressed by a single base SI unit. For example, when talking about density, we must use volume/mass. Mass has its own SI unit, the gram. However, volume does not. Volume is expressed with a derived SI unit, the meter cubed. As a result, the unit for density is [math]\displaystyle{ \mathrm{m}^3/\mathrm{g} }[/math] . Those units are called derived SI units. Units can be combined to create a new unit. Some frequently-used combinations have their units named. Here are some examples:

• Watt (W), the unit of power.
  • [math]\displaystyle{ \mathrm{W} = \mathrm{J}/\mathrm{s} \ }[/math]

• Pascal (Pa), the unit of pressure.
  • [math]\displaystyle{ \mathrm{Pa} = \mathrm{N}/\mathrm{m}^2 \ }[/math]

• Hertz (Hz), the unit of frequency.
  • [math]\displaystyle{ \mathrm{Hz} = 1/\mathrm{s} = \mathrm{s}^{-1} \ }[/math]

• Newton (N), the unit of force.
  • [math]\displaystyle{ \mathrm{N} = \mathrm{kg} \cdot \mathrm{m}/\mathrm{s}^2 }[/math]

• Joule (J), the unit of energy.
  • [math]\displaystyle{ \mathrm{J} = \mathrm{N} \cdot \mathrm{m} = \mathrm{kg} \cdot \mathrm{m}^2/\mathrm{s}^2 }[/math]

• Coulomb (C), the unit of electric charge.
  • [math]\displaystyle{ \mathrm{C} = \mathrm{A} \cdot \mathrm{s} }[/math]

• Volt (V), the unit of electric potential or voltage.
  • [math]\displaystyle{ \mathrm{V} = \mathrm{J}/\mathrm{C} = \mathrm{W}/\mathrm{A} \ }[/math]

Connectedness

This topic can be applied to every aspect of science. When solving a problem, or even when doing research, all equations and theories are based on SI units. It is an agreement between scientists internationally to use these units to reduce errors or misunderstanding. Therefore, it is very important to understand the concept of SI units when doing any work related to the sciences. Indeed, this topic is connected to not only physics but also every other scientific subject, such as chemistry. In addition, although it may not have daily use in the United States, SI is a regular part of life in other countries around the world, and familiarity with this system will make adaptation easier when traveling internationally.

History

The creation of the decimal Metric System at the time of the French Revolution and the subsequent deposition of two platinum standards representing the meter and the kilogram, on 22 June 1799, in the Archives de la Republic in Paris can be seen as the first step in the development of the present International System of Units. In 1832, Gauss strongly promoted the application of this Metric System, together with the second defined in astronomy, as a coherent system of units for the physical sciences. Gauss was the first to make absolute measurements of the earth’s magnetic force in terms of a decimal system based on the three mechanical units 'millimeter', 'gram', and 'second' for, respectively, the quantities length, mass and time. In later years, Gauss and Weber extended these measurements to include electrical phenomena.

Further reading

SI Units for Clinical Measurement 1st Edition by Donald S. Young

Matter & Interactions, Vol. I: Modern Mechanics, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)

References

http://physics.nist.gov/ National institute of standards and Technology.

http://wps.prenhall.com/wps/media/objects/165/169061/blb9ch0104.html Pearson educational site.

Matter & Interactions, Vol. I: Modern Mechanics, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)

Tutorial & Drill Problems for General Chemistry (and Intro) By Walter S. Hamilton, Ph.D.