Escape Velocity

A diagram showing several orbits around Earth. Orbit [math]\displaystyle{ p }[/math] is a parabolic orbit, with the object travelling at escape velocity. Orbit [math]\displaystyle{ H }[/math] is an example of the hyperbolic orbit of an object travelling faster than the escape velocity.

Escape velocity is defined as the minimum velocity required for an object to escape the gravitational force of a large object. The sum of an object's kinetic energy and its gravitational potential energy is equal to zero. The gravitational potential energy is negative due to the fact that kinetic energy is always positive. The velocity of the object will be be zero at infinite distance from the center of gravity. There is no net force on an object as it escapes and zero acceleration is perceived.

The Main Idea

The formula for escape velocity at a givendistance from a body is calculated by the formula

[math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}}, }[/math]

where [math]\displaystyle{ G }[/math] is the universal gravitational constant ([math]\displaystyle{ G = 6.7\times 10^{-11} \text{N}\cdot\text{m}^2 / \text{kg}^2 }[/math]), [math]\displaystyle{ M }[/math] is the mass of the large body to be escaped, and [math]\displaystyle{ r }[/math] the distance from the center of mass of the mass [math]\displaystyle{ M }[/math] to the object. This equation assumes there are no other forces acting on either body. As a side note, the escape velocity stated here could really be called escape speed due to the fact that the quantity is independent of direction. Notice that the equation does not include the mass of the orbiting body.

A Mathematical Model

When we model escape velocity, we consider the situation when an object's velocity takes it to a point an infinite distance away. The lowest possible escape velocity has a final speed of zero, and any speed higher results in a nonzero final speed. To derive the formula for the escape velocity, the energy principle is used, and we assume that the only two objects in our system are the orbiting body and the planet.

In our system , the energy principle states that

[math]\displaystyle{ (K + U_g)_i = (K + U_g)_f \, }[/math]

When finding the minimum escape velocity, [math]\displaystyle{ K-f = 0 }[/math] because we take the final velocity to be zero, and [math]\displaystyle{ U_{gf} = 0 }[/math] because its final distance is expressed as infinity, therefore

[math]\displaystyle{ (K + U_g)_i = \frac{1}{2}mv_e^2 + \frac{-GMm}{r} = 0 }[/math]

Solving for [math]\displaystyle{ v_e }[/math] yields:

[math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}} }[/math]

Note that because both the kinetic and potential energy terms contain a common factor [math]\displaystyle{ m }[/math], the final escape velocity is independent of the mass of the orbiting body.

Bound versus unbound systems

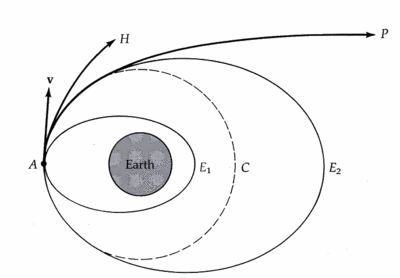
When an object is orbiting a massive body, it can be in one of two states: bound and unbound. If the object is in a bound state, we see an elliptical trajectory, in which the orbiting body never escapes the gravitational influence of the more massive body. In an unbound state, however, we observe a parabolic or hyperbolic trajectory, in which the object is able to escape the gravitational influence of the orbiting body and escape to infinity. The diagram to the left shows an unbound system, in which the sum of the kinetic and potential energy of the orbiting body is greater then 0. As distance goes to infinity in this system, gravitational potential energy approaches zero, but the object retains a positive kinetic energy, and therefore a positive velocity. The image on the right shows a bound system, in which the sum of the kinetic and potential energy is negative. In this system, kinetic energy reaches zero at a specific maximum distance, at which point the object begins to fall back towards the massive body, never to escape.

The energy diagram of an unbound system, in which the object has excess kinetic energy. The vertical axis represents energy, while the horizontal axis represents distance. At exactly the escape velocity, the sum of [math]\displaystyle{ K }[/math] and [math]\displaystyle{ U }[/math] is exactly 0.

The energy diagram of a bound system, in which the object has insufficient kinetic energy to escape. The vertical axis represents energy, while the horizontal axis represents distance.

Examples

Escaping Jupiter

The radius of Jupiter is [math]\displaystyle{ 71.5\times 10^6 \text{m} }[/math], and its mass is [math]\displaystyle{ 1900\times 10^{24} \text{kg} }[/math]. What is the escape speed of an object launched straight up from just above the atmosphere of Jupiter?

System = Jupiter + object [math]\displaystyle{ \Delta E = 0\\ v_i = ?\\ v_f = 0 \text{m/s}\\ r_i = 71.5\times 10^6 \text{m}\\ r_f = \infty\\ m = m_{Object}\\ M = m_{Jupiter} = 1900\times 10^{24} \text{kg} \\ }[/math]

Starting from the Energy Principle:

[math]\displaystyle{ \Delta E = W + Q\\ \Delta E = 0 + 0 = 0\\ \Delta K + \Delta U = 0\\ \frac{1}{2}m(v_f^2-v_i^2) + (\frac{-GMm}{r_f} - \frac{-GMm}{r_i}) = 0\\ \frac{1}{2}m(0-v_i^2) + (0 - \frac{-GMm}{r_i}) = 0\\ -\frac{1}{2}mv_i^2 + \frac{GMm}{r_i} = 0\\ \frac{GMm}{r_i} = \frac{1}{2}mv_i^2\\ \frac{GM}{r_i} = \frac{1}{2}v_i^2\\ v_i = \sqrt{\frac{2GM}{r_i}}\\ = \sqrt{\frac{2(6.7\times 10^{-11} \text{N}\cdot\text{m}^2 / \text{kg}^2)(1900\times 10^{24} \text{kg})}{(71.5\times 10^6 \text{m})}}\\ = 5.97 \times 10^4 \text{m/s} }[/math]

Escaping Earth

Compute the escape velocity for Earth if its mass is [math]\displaystyle{ 5.98 \times 10^{24} \text{kg} }[/math] and its radius is [math]\displaystyle{ 6.37 \times 10^{6} \text{m} }[/math]. [math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}} \\ = \sqrt{\frac{2(6.7\times 10^{-11} \text{N}\cdot\text{m}^2 / \text{kg}^2)(5.98\times 10^{24} \text{kg})}{(6.37\times 10^6 \text{m})}}\\ = 1.12 \times 10^4 \text{m/s} }[/math]

Connectedness

In real life, escape velocity is not as easy to calculate as in the above examples. The primary complicating factor is the fact that there are more than two bodies in the universe, so in systems with multiple massive attracting bodies, escape velocity can become more complicated. One example is the escape velocity of an object from Earth: an object that achieves the escape velocity of Earth could theoretically escape Earth's influence, but it would remain in orbit around the sun unless its speed were much greater. The concept of escape velocity is widely used in orbital mechanics and rocketry and is critical for the planning of space missions.

External links

http://www.scientificamerican.com/article/bring-science-home-reaction-time/

https://www.youtube.com/watch?v=7w56rwAtUZU

References

"Escape Velocity | Physics." Encyclopedia Britannica Online. Encyclopedia Britannica, n.d. Web. 05 Dec. 2015. [1]

Giancoli, Douglas C. "Physics for Scientists and Engineers with Modern Physics." Google Books. Google, n.d. Web. 05 Dec. 2015. [2]

"Escape Velocity." Wikipedia. Wikimedia Foundation, n.d. Web. 05 Dec. 2015. [3]

Velocity, Escape, and ©200. ESCAPE VELOCITY EXAMPLES (n.d.): n. pag. 13 June 2003. Web. 5 Dec. 2015. [4]