RC Circuit: Difference between revisions
Mrussell38 (talk | contribs) |
Mrussell38 (talk | contribs) No edit summary |
||
| Line 70: | Line 70: | ||
<math>{τ} = {RC}</math> | <math>{τ} = {RC}</math> | ||
==A Computational Model== | ===A Computational Model=== | ||
Using a simulation where R and C were equal, the capacitors were charged and then discharged and the two images show the voltage and current of this versus time. | Using a simulation where R and C were equal, the capacitors were charged and then discharged and the two images show the voltage and current of this versus time. | ||
| Line 87: | Line 87: | ||
===Simple=== | ===Simple=== | ||
In a circuit where time t = RC, the factor <math>{e^{\frac{-t}{RC}}}</math> has fallen from value <math>{e^0} = {1}</math> to the value: | |||
In the | |||
e^(-t/RC) = e^1 = 1/e = 1/2.718 = 0.37 | |||
Calculate the time constant for the RC circuit with R = 12 ohms and C = 1 farad. | |||
Solution: | |||
<math> {RC}= {12*1} = {12 seconds}</math> | |||
===Middling=== | |||
Using the information from the problem above: | |||
Show that the power dissipated in the bulb at t=RC is only 14% of the original power? | |||
Solution: | Solution: | ||
Using <math>{IΔV} = {RI^2}</math>, reduction in current by factor of 0.37 gives a reduction in power by a factor of (0.37)^2 = 0.1369 | |||
a.) What | ===Difficult=== | ||
Suppose one wished to capture the picture of a bullet (moving at 0.04 m/s ) that was passing through an orange. The duration of the flash is related to the RC time constant, τ . What size capacitor would one need in the RC circuit to succeed, if the resistance of the flash tube was 10.0 Ω? Assume the oragne is a sphere with a diameter of 0.08 m. | |||
Solution: | Solution: | ||
You know the velocity of the bullet and the distance. You can find the time using Physics I principles such as <math>{time} = {\frac{distance}{velocity}} = {\frac{.08}{.04}} = {.0032 seconds} </math> | |||
the time becomes equal to τ, so: | |||
<math>{C} = {\frac{τ}{v}} = {\frac{0.0032}{10Ω}} = {32μF} </math> | |||
==Connectedness== | ==Connectedness== | ||
1. How is this topic connected to something that you are interested in? | 1. How is this topic connected to something that you are interested in? | ||
:: I like listening to music and RC currents are used in subwoofers in my car and other audio equipment. | :: I like listening to music and RC currents are used in subwoofers in my car and other audio equipment. | ||
2. How is it connected to your major? | 2. How is it connected to your major? | ||
:: I'm an ISyE major and RC currents are directly related to every job, but in warehouses | :: I'm an ISyE major and RC currents are directly related to every job, but in warehouses where heavy machinery and appliances are involved, RC currents are used in parts either at the warehouse or ones that are being assembled. | ||
3. Is there an interesting industrial application? | 3. Is there an interesting industrial application? | ||
:: RC circuits are used to hear certain sounds so that in an assembly line something can be sorted or passed through to another area. | :: RC circuits are used to hear certain sounds so that in an assembly line something can be sorted or passed through to another area. | ||
==History== | |||
The RC circuits have been in use for a long time. Georg Simon Ohm, was someone who spent alot of time researching RC Circuits and Ohm's Law was founded by him. He did his work from 1830s-1840s and he received recognition after a long time of being mocked by other scientists. | |||
== See also == | == See also == | ||
Revision as of 22:53, 17 April 2016
CLAIMED BY MARK RUSSELL SPRING 2016

The Main Idea
An RC circuit is a circuit that contains a battery with a known emf, a resistor (R), and a capacitor (C). An RC circuit can be in either series or parallel. The figure in the top right of the page shows an RC circuit. The capacitor stores electric charge (Q)
RC Circuits use a DC (direct current) voltage source and the capacitor is uncharged at its initial state. In the figure below, you see an RC circuit with a switch. When the switch is closed, the capacitor will begin to charge as the current can now flow throughout the circuit. To discharge the capacitor, you simply disconnect the switch.

Remember that potential difference across the capacitor is delta [math]\displaystyle{ {V} = {Q}/{C} }[/math], where Q is charge on the plate and C is the capacitance. When the switch is closed, voltage on the capacitor rises rapidly at first, due to the high current at [math]\displaystyle{ {time} = {0} }[/math]. The voltage opposes the battery, increasing from zero to the max emf when the capacitor is fully charged. The current decreases from its initial value of [math]\displaystyle{ {I}_{0} = {emf}/{R} }[/math] to zero as the voltage on the capacitor reaches the same value as the emf. The current is initially at its max at time [math]\displaystyle{ {t} = {0} }[/math]. Once the potential difference across the plates of the capacitor equals the battery's voltage supply, current will stop flowing through the circuit. This is known as the steady state of an RC circuit; it is reached when time goes to infinity.
Using derived calculus, the equation for voltage versus time when the capacitor is charged through resistor R is [math]\displaystyle{ {V} = {emf(1-e^{\frac{-t}{RC}})} }[/math]. [math]\displaystyle{ {V} }[/math] is defined as the voltage across the capacitor. [math]\displaystyle{ {emf} }[/math] is equal to the emf of the DC voltage source. The units of [math]\displaystyle{ {RC} }[/math] are in seconds. [math]\displaystyle{ {τ} = {RC} }[/math]. [math]\displaystyle{ {τ} }[/math] is the constant of time in the RC circuit.
The smaller the resistance, the faster a capacitor will be charged. It takes longer to charge than to discharge. This is because a larger current flows through a smaller resistance ([math]\displaystyle{ {I} = {V/R} }[/math]). Also the smaller the capacitor (C), the less time it will need to charge. [math]\displaystyle{ {τ} = {RC} }[/math] explains both of these.
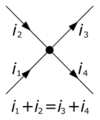
Kirchoff's Node Rule is important to RC Circuits because finding the current flow in the different states of an RC Circuit often relies on nodes when the capacitor is in a parallel circuit.
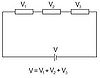
Kirchhoff’s loop rule explains that the sum of changes in potential around any closed loop must be zero.
A Mathematical Model
These three equations are helpful in solving and understanding RC circuit problems
[math]\displaystyle{ {ΔV}_{round trip} = {0} }[/math]
[math]\displaystyle{ {ΔV} = {I}{R} }[/math]
[math]\displaystyle{ {Q} = {C}{V} }[/math]
In a loop of a circuit, the change of potential difference has to be zero. The energy equation for the RC Circuit in the figure at the top of the page is:
[math]\displaystyle{ {ΔV}_{round trip} = emf-RI-Q/C = 0 }[/math]
At the final state of the circuit after the current has dropped to zero and the capacitor is fully charged, [math]\displaystyle{ {RI} = {0} }[/math]. The new equation for the final state is:
[math]\displaystyle{ {V}_{round trip} = emf-Q/C = 0 }[/math]
[math]\displaystyle{ {Q} = emf*C }[/math]
To find the equation for voltage versus time when charging a capacitor through a resistor, you start with rearranging the energy equation and solving for I:
[math]\displaystyle{ {I} = {\frac{dQ}{dt}}={\frac{emf-Q/C}{R}} }[/math]
You know that [math]\displaystyle{ {I} = {\frac{dQ}{dt}} }[/math] due to the rate at which charge builds up the positive capactior plate.
[math]\displaystyle{ {I} = {\frac{dQ}{dt}}={\frac{emf-Q/C}{R}} }[/math]
If you exponentiate both sides, the following equation is achieved.
[math]\displaystyle{ {\frac{IR}{emf}} = {e^{\frac{-t}{RC}}} }[/math]
[math]\displaystyle{ {I} = {\frac{emf}{R}e^{\frac{-t}{RC}}={\frac{dQ}{dt}}} }[/math]
[math]\displaystyle{ {dQ} = \int_0^t{\frac{emf}{R}e^{\frac{-t}{RC}}\,\mathrm{d}t} }[/math]
[math]\displaystyle{ {Q} = {C(emf)(1-e^{\frac{-t}{RC}})} }[/math].
Since [math]\displaystyle{ {V} = {Q/C} }[/math], thus
[math]\displaystyle{ {V} = {emf(1-e^{\frac{-t}{RC}})} }[/math].
This is the formula for the change in voltage of a series RC circuit with respect to time.
The RC time constant formula is:
[math]\displaystyle{ {τ} = {RC} }[/math]
A Computational Model
Using a simulation where R and C were equal, the capacitors were charged and then discharged and the two images show the voltage and current of this versus time.
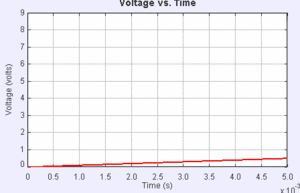
For the gif below, the capacitor is charged and then discharged. This shows the voltage over time. The red line is the voltage and the gray line is the emf. (May have to click image to see gif)
For the gif below, the capacitor is charged and then discharged. This shows the current over time. The blue line is the current. (May have to click image to see gif)
Examples
Simple
In a circuit where time t = RC, the factor [math]\displaystyle{ {e^{\frac{-t}{RC}}} }[/math] has fallen from value [math]\displaystyle{ {e^0} = {1} }[/math] to the value:
e^(-t/RC) = e^1 = 1/e = 1/2.718 = 0.37
Calculate the time constant for the RC circuit with R = 12 ohms and C = 1 farad.
Solution:
[math]\displaystyle{ {RC}= {12*1} = {12 seconds} }[/math]
Middling
Using the information from the problem above:
Show that the power dissipated in the bulb at t=RC is only 14% of the original power?
Solution:
Using [math]\displaystyle{ {IΔV} = {RI^2} }[/math], reduction in current by factor of 0.37 gives a reduction in power by a factor of (0.37)^2 = 0.1369
Difficult
Suppose one wished to capture the picture of a bullet (moving at 0.04 m/s ) that was passing through an orange. The duration of the flash is related to the RC time constant, τ . What size capacitor would one need in the RC circuit to succeed, if the resistance of the flash tube was 10.0 Ω? Assume the oragne is a sphere with a diameter of 0.08 m.
Solution:
You know the velocity of the bullet and the distance. You can find the time using Physics I principles such as [math]\displaystyle{ {time} = {\frac{distance}{velocity}} = {\frac{.08}{.04}} = {.0032 seconds} }[/math]
the time becomes equal to τ, so:
[math]\displaystyle{ {C} = {\frac{τ}{v}} = {\frac{0.0032}{10Ω}} = {32μF} }[/math]
Connectedness
1. How is this topic connected to something that you are interested in?
- I like listening to music and RC currents are used in subwoofers in my car and other audio equipment.
2. How is it connected to your major?
- I'm an ISyE major and RC currents are directly related to every job, but in warehouses where heavy machinery and appliances are involved, RC currents are used in parts either at the warehouse or ones that are being assembled.
3. Is there an interesting industrial application?
- RC circuits are used to hear certain sounds so that in an assembly line something can be sorted or passed through to another area.
History
The RC circuits have been in use for a long time. Georg Simon Ohm, was someone who spent alot of time researching RC Circuits and Ohm's Law was founded by him. He did his work from 1830s-1840s and he received recognition after a long time of being mocked by other scientists.
See also
Further reading
External links
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/rcimp.html
http://buphy.bu.edu/~duffy/semester2/c11_RC.html
References
http://www.compadre.org/portal/items/detail.cfm?ID=9986
https://www.pa.msu.edu/courses/1997spring/PHY232/lectures/kirchoff/examples.html