Right-Hand Rule

CLAIMED BY AMIRA ABADIR (Spring 2016)

CLAIMED BY Kavin Somu (Fall 2016)

The Main Idea

The Right-Hand Rule is an easy way to find the direction of a cross product interaction before doing the math. For any equation involving a cross product, the right hand rule is a valuable tool for finding the direction. There are two primary ways of using the right hand rule. The first method is to use your entire hand. In the example below, the velocity is pointing north up and the magnetic field is pointing to the left. We place our hand with your thumb sticking up along the velocity since thats the first variable in F= qv X B. You curl your fingers towards the magnetic field. Your thumb is pointing upwards hence the direction of magnetic force is going out of the page. It is important to note that this only applies to positive charges. However, it is still very easy to find the direction of the right hand rule for negative charges. It is just the opposite direction for what you would do for positive charges.

A Mathematical Model

The Right-Hand Rule is mathamatically modeled by the cross product:

[math]\displaystyle{ \mathbf{u\times v}=(u_2v_3\mathbf{i}+u_3v_1\mathbf{j}+u_1v_2\mathbf{k}) -(u_3v_2\mathbf{i}+u_1v_3\mathbf{j}+u_2v_1\mathbf{k}) }[/math]

A Computational Model

The cross product is used to describe many magnetic interactions, for example, magnetic field created by a moving charge or a current and magnetic force on a particle by a magnetic field. Because of this, using the right hand rule, to determine the direction of a cross product, can be a useful to check behind the math for sign errors.

Follow the chart bellow to find which fingers correspond to which vectors.

[math]\displaystyle{ \mathbf{A\times B}=\mathbf{C} }[/math]

Vector	Right-hand	Right-hand (alternative)
A	First or index	Thumb
B	Second finger or palm	First or index
C	Thumb	Second finger or palm

Another method for determining the direction of the product orthogonal vector is to place the fingers of your right hand in the direction of the first vector(A). Curl your fingers in the direction of the second vector(B), effectively making the "thumbs up" sign in whichever direction the thumb happens to be pointing. The resulting vector(C) is in the direction in which your thumb is now pointing.

Examples

Magnetic Force on a Moving Particle

[math]\displaystyle{ \mathbf{F} = q\mathbf{v} \times \mathbf{B} }[/math]

The direction of the cross product may be found by application of the right hand rule as follows:

1. The index finger points in the direction of the momentum vector qv.
2. The middle finger points in the direction of the magnetic field vector B.
3. The thumb points in the direction of magnetic force F.

For example, for a positively charged particle moving to the right, in a region where the magnetic field points up, the resultant force points out of the page.

Magnetic Field made by a Current

[math]\displaystyle{ \mathbf{B} = \frac{\mu_0I}{4\pi}\int_{\mathrm{wire}}\frac{\mathrm{d}\boldsymbol{\ell} \times \mathbf{\hat r}}{r^2}, }[/math]

The direction of the cross product may be found by application of the right hand rule as follows:

1. The thumb points in the direction of current I.
2. The index finger points in the direction of the observation vector r.
3. The middle finger points in the direction of the magnetic field vector B.

Force on a Current from a Magnetic Field

[math]\displaystyle{ \mathbf{F} = \mathbf{I} \times \mathbf{B} }[/math]

The direction of the cross product may be found by application of the right hand rule as follows:

1. The index finger points in the direction of the current I.
2. The middle finger points in the direction of the magnetic field vector B.
3. The thumb points in the direction of magnetic force F.

For example, for a current moving into the page, in a region where the magnetic field points up, then the force is to the right of the current.

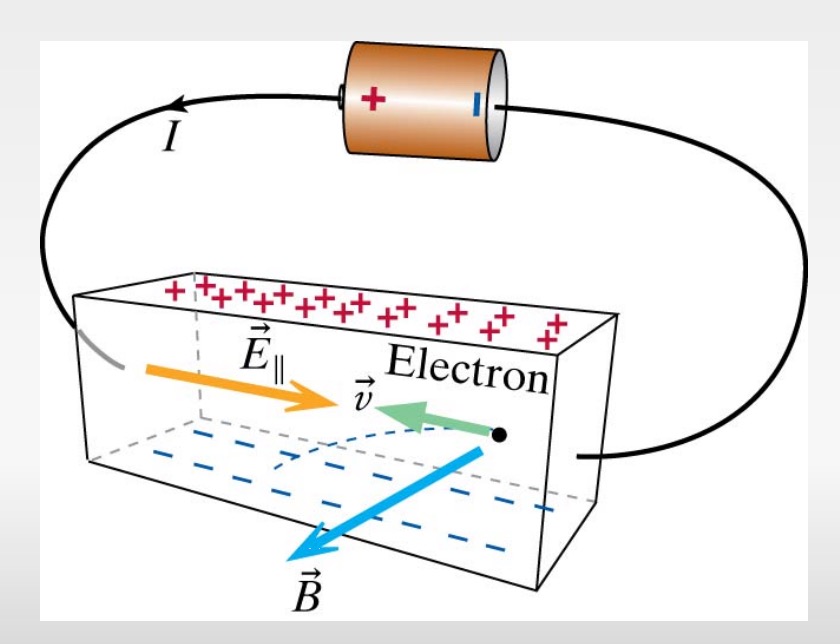
Hall Effect Example

In the above picture, you see that all the positive charges accumulated at the top and all the negative charges accumulated to the bottom. You know the direction the particles velocity and magnetic field. Can you find out the charge of the particle using the right hand rule?

In the picture, the particles are coming out of the negative terminal, so they are electrons. This can be verified by using the right hand rule. You curl your fingers from velocity vector to magnetic field vector to find the direction of magnetic force perpendicular. Your thumb is pointing up, but since these are negative charges, its opposite and you flip your hand and you find that the direction of the magnetic force is actually pointing down. Therefore it makes sense that the electrons would accumulate at the bottom since its magnetic force is pushing them towards there.

Connectedness

1. How is the topic connected to something you are interested in?

I am interested in its application to the Hall Effect on how charges accumulate in a conductor. I just fine it so interesting that such a simple tool allows us to find the direction of forcess, moving objects, and many other useful applications.

2. How is it connected to your major?

As an industrial engineer, it has little application directly however, for those working in engineering physics and need to come up with a design. They could run into problems involving forces and velocity that require the right hand rule.

History

John Ambrose Fleming is credited with devising the right hand rule. He was a professor at the University College, London where he was liked by many of his students. He taught them how to easily determine the direction of a current. He made directional relationships easier between current, its magnetic field, and the electromotive force.

See Also

External Links

1. https://www.khanacademy.org/test-prep/mcat/physical-processes/magnetism-mcat/a/using-the-right-hand-rule
2. https://ocw.mit.edu/courses/physics/8-02t-electricity-and-magnetism-spring-2005/lecture-notes/prs_w06d1.pdf
3. http://physics.bu.edu/~duffy/semester2/d12_RHR_practice.html

References

1. https://en.wikipedia.org/wiki/Right-hand_rule
2. https://en.wikipedia.org/wiki/Magnetic_field
3. https://nationalmaglab.org/education/magnet-academy/history-of-electricity-magnetism/pioneers/john-ambrose-fleming

--Cjacobson7 (talk) 13:45, 10 November 2015 (EST)