Field of a Charged Ball

By Eric Erwood Claimed by Andrea Diaz (Fall 2016)

In this section, the electric field of a charged ball will be discussed.

The Main Idea

In this section, we will focus on a scenario where a ball has charge distributed throughout its volume. Calculating the electric field both outside and inside the sphere will be addressed.

A Mathematical Model

Step 1: Given a solid charged sphere throughout its volume, the first step is to cut up the the sphere into pieces. As a result, the solid sphere will appear as a series of spherical shells.

Step 2: Relationship between r and R. Next, it is necessary to determine whether the observation point is outside or inside the sphere.

If r>R, then we are outside the sphere. All the spherical shells appear as point charges at the center of the sphere. As a result, the electric field outside the sphere is a point charge:

[math]\displaystyle{ \vec E=\frac{1}{4 \pi \epsilon_0}\frac{Q}{r^2} \hat r }[/math] when r>R, and R is the radius of the sphere.

However, when r<R, the observation location is inside some of the shells but outside others. To find [math]\displaystyle{ \vec E_{net} }[/math], add the contributions to the electric field from the inner shells. After adding the contributions of each inner shell, you should have an electric field equal to:

[math]\displaystyle{ \vec E = \frac{1}{4 \pi \epsilon_0}\frac{\Delta Q}{r^2} }[/math]

We find [math]\displaystyle{ \Delta Q }[/math]:

[math]\displaystyle{ \Delta Q = Q \frac{\text {volume of inner shells}}{\text {volume of sphere}} = Q \frac{\frac{4}{3} \pi r^3}{\frac{4}{3} \pi R^3} }[/math]

We find that:

[math]\displaystyle{ \vec E = \frac{1}{4 \pi \epsilon_0}\frac{Q}{r^2}\frac{\frac{4}{3} \pi r^3}{\frac{4}{3} \pi R^3} = \frac{1}{4 \pi \epsilon_0}\frac{Q}{R^3}r }[/math]

The charge inside the sphere is proportional to r. When r=R,

[math]\displaystyle{ \vec E = \frac{1}{4 \pi \epsilon_0}\frac{Q}{R^2} }[/math]

A Computational Model

https://trinket.io/glowscript/48f6efd07a

use this code to see how it looks, change the r value.

Examples

Simple

A sphere is charged throughout it's volume with a charge of Q= 6e-5 C. The radius of the this sphere is R=10. Find the electric field created by a sphere of radius r=4.

Step 1: cut up the sphere into shells

step 2: we know that r<R

Next find [math]\displaystyle{ \Delta Q }[/math]:

[math]\displaystyle{ \Delta Q = Q \frac{\text {volume of inner shells}}{\text {volume of sphere}} = Q \frac{\frac{4}{3} \pi r^3}{\frac{4}{3} \pi R^3} }[/math]

[math]\displaystyle{ \vec E = \frac{1}{4 \pi \epsilon_0}\frac{Q}{r^2}\frac{\frac{4}{3} \pi r^3}{\frac{4}{3} \pi R^3} = \frac{1}{4 \pi \epsilon_0}\frac{Q}{R^3}r }[/math]

[math]\displaystyle{ \vec E = \frac{1}{4 \pi \epsilon_0}\frac{Q}{R^3}r = 9e9 * \frac{6*10^{-5} C}{(10m)^3}*4m = 2160 N/C }[/math]

Difficult

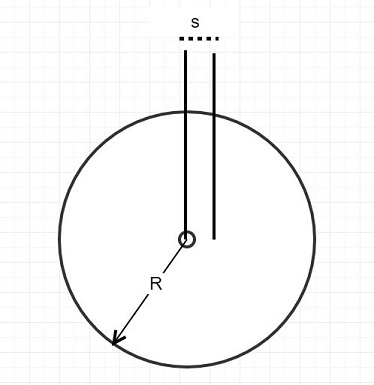
A simplified model of a hydrogen atom is that the electron cloud is a sphere of radius R with uniform charge density and total charge −e. (The actual charge density in the ground state is nonuniform.)

For the uniform-density model, calculate the polarizability α of atomic hydrogen in terms of R. Consider the case where the magnitude E of the applied electric field is much smaller than the electric field required to ionize the atom. Suggestions for your analysis: Imagine that the hydrogen atom is inside a capacitor whose uniform field polarizes but does not accelerate the atom. Consider forces on the proton in the equilibrium situation, where the proton is displaced a distance s from the center of the electron cloud

(s « R in the diagram). (Use the following as necessary: R and ε0.)

Useful equations:

[math]\displaystyle{ \vec p = \alpha *E }[/math]

[math]\displaystyle{ \vec p = Q*s }[/math]

Assume an applied electric field of strength E. This electric field polarized the hydrogen atom. Now there is a spherical charge of radius s. Use the volume ratio, and then use the useful equations to find [math]\displaystyle{ \alpha }[/math]

[math]\displaystyle{ \vec E = \frac{1}{4 \pi \epsilon_0}\frac{e}{s^2}\frac{\frac{4}{3} \pi s^3}{\frac{4}{3} \pi R^3} = \frac{1}{4 \pi \epsilon_0}\frac{e}{R^3}s }[/math]

[math]\displaystyle{ \alpha = \frac{e*s}{\frac{1}{4 \pi \epsilon_0}\frac{e}{R^3}s} = 4\pi \epsilon_0 R^3 }[/math]

Looking Ahead, Gauss's Law

Later in this wikibook, you will learn about Gauss's Law. This will make calculating the electric field easier.

The formula for Gauss's Law is:

[math]\displaystyle{ \oint \vec E \bullet \hat n dA = \frac{1}{\epsilon_0}\Sigma Q_{\text {inside the surface}} }[/math]

Using this, one can calculate the the electric field when r<R for a solid sphere charged throughout.

[math]\displaystyle{ \vec E * 4\pi*r^2= \frac{1}{\epsilon_0}Q\frac{\frac{4}{3} \pi r^3}{\frac{4}{3} \pi R^3} }[/math]

[math]\displaystyle{ \vec E = \frac{1}{4 \pi \epsilon_0}\frac{Q}{R^3}r }[/math]

See also

Further reading

http://www.physicsbook.gatech.edu/Point_Charge

http://www.physicsbook.gatech.edu/Electric_Dipole

http://www.physicsbook.gatech.edu/Gauss%27s_Flux_Theorem

References

This section contains the the references you used while writing this page

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elesph.html

https://www.physicsforums.com/threads/calculate-the-polarizability-a-lpha-of-atomic-hydrogen-in-terms-of-r.339994/

Matter and Interactions, 4th Edition: 1-2