Inclined Plane: Difference between revisions
No edit summary |
No edit summary |
||
| Line 16: | Line 16: | ||
[[File:Inclined_example3.png]] | [[File:Inclined_example3.png]] | ||
== | ==Diagram of the Inclined Plane== | ||
[[File:physics_inclined.png]]<br> | [[File:physics_inclined.png]]<br> | ||
θ= Angle of the plane to the horizontal<br> | θ= Angle of the plane to the horizontal<br> | ||
| Line 26: | Line 26: | ||
mgCosθ= A force acting into the plane (opposite to N) | mgCosθ= A force acting into the plane (opposite to N) | ||
==Mechanical Advantage== | |||
'''Fw''' is a gravitational force that applies on the plane<br> | '''Fw''' is a gravitational force that applies on the plane<br> | ||
'''Fi''' is a force exerted on the object and parallel to the plane<br> | '''Fi''' is a force exerted on the object and parallel to the plane<br> | ||
:<math>\mathrm{MA} = \frac{F_w}{F_i}. \,</math><br> | :<math>\mathrm{MA} = \frac{F_w}{F_i}. \,</math><br> | ||
==Terminology== | |||
Slope: A slope brings a mechanical advantage to the incline plane. | |||
:<math>\theta = \tan^{-1} \bigg( \frac {\text{Rise}}{\text{Run}} \bigg) \,</math> | |||
Revision as of 00:32, 27 November 2016
Claimed by Sunmin Kim Skim883 (Fall2016)
Definition
inclined(adj): deviating in direction from the horizontal or vertical; sloping
plane(n):a flat or level surface
Inclined plane means a plane with a level surface. It is inclined at a angle to the horizontal.
Why do we need to know?
When we solve physics problems, it is necessary to understand free diagram.
Understanding this inclined plane will help you apply gravity and angles on calculating forces.
Uses
You may see this almost every day in your daily life. The inclined planes are needed for loading and unloading heavy goods on transportation such as ships, trucks and planes because it has mechanical advantage of reducing the forces required to move heavy goods.
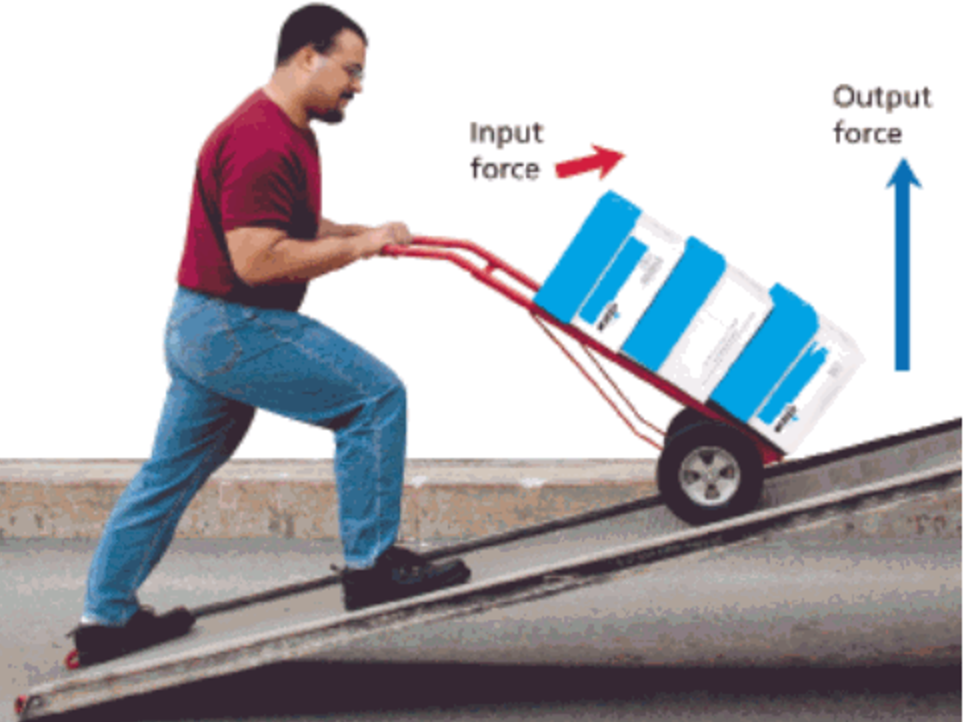


Diagram of the Inclined Plane
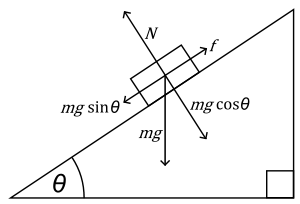
θ= Angle of the plane to the horizontal
g= Acceleration due to gravity
m= Mass of object
N= Normal force (perpendicular to the plane)
f = frictional force of the inclined plane (sometimes it is omitted on test problems)
mgSinθ= A force parallel to the plane (mgSinθ > f the body slides down the plane)
mgCosθ= A force acting into the plane (opposite to N)
Mechanical Advantage
Fw is a gravitational force that applies on the plane
Fi is a force exerted on the object and parallel to the plane
- [math]\displaystyle{ \mathrm{MA} = \frac{F_w}{F_i}. \, }[/math]
Terminology
Slope: A slope brings a mechanical advantage to the incline plane.
- [math]\displaystyle{ \theta = \tan^{-1} \bigg( \frac {\text{Rise}}{\text{Run}} \bigg) \, }[/math]