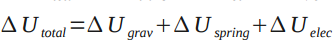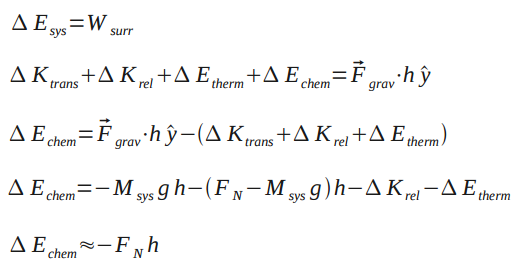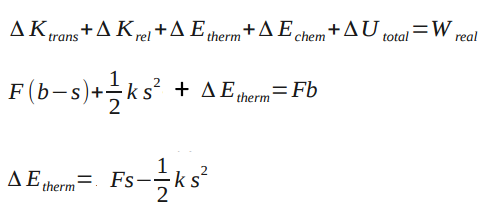Real Systems

The Main Idea

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

In Point Particle Systems, the only change in energy is from translational kinetic energy because every force is assumed to act on the center of mass. Up until Week 10, we have been measuring change in energy of systems using the Point Particle Method. From what we learned in Week 10 though, we know that translational kinetic energy is not the only type of energy there can be a change in (see: Thermal Energy and Translational, Rotational and Vibrational Energy). In a real system, you must consider the point of application of each force when calculating the change in energy. Also in real systems, forces may also occur over a different displacement than the displacement of the center of mass. These two key differences lead to an interesting mathematical model that differs from that used for the Point Particle Method.

A Mathematical Model

The mathematical equation used for Real Systems can vary depending on what his happening within and on the system. For the sake of flow with the WikiPhysicsBook, we will be analyzing real systems with the energy principle.

(We are ignoring Q for the sake of simplicity. It will not be taken into account in the subsequent examples despite the possible transfer of energy from temperature differences). E is the total energy of the system and W is the net work done from the surroundings on system. The major difference of a point particle system versus a real system is in the calculation of Work. In a point particle system, it is calculated by the net force dot product with the change in the position of the center of mass. However, Work in a real system is calculated by:

This means that the summation of the all the external forces dot product with the distance each force was applied amounts to the total change in energy of the real system. The change in the mathematical equation for Work between a point particle system and a real system is important because now different forms of energy may be taken into account. In a real system, the change in energy of a system can be given by:

Where, total change in internal energy (U) is given by:

total change in kinetic energy (K) is given by:

and change in Miscellaneous Energy is given by:

Examples

In order to better display the difference of Real Systems from Point Particle Systems, the examples done here will be the same examples done from Point Particle Systems.

Jumper Model (Simple)

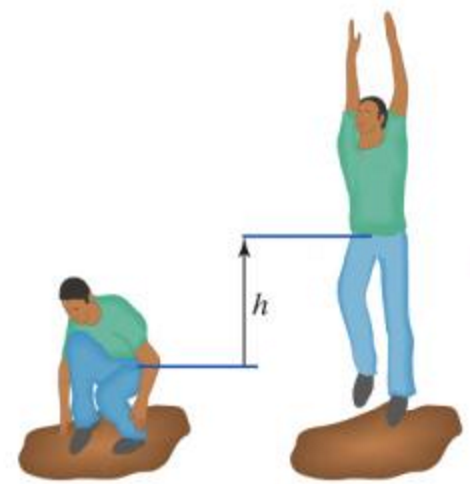Problem: You jump up so that your center of mass has moved a distance h. How much chemical energy did you expend?

From the Point Particle System analysis, we know that and .

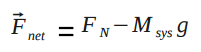
System: Person Surroundings: Earth+Floor

Initial State: Crouched down

Final State: Extended and moving with speed v

Assuming negligent change in thermal energy and relative kinetic energy, the change in thermal energy is approximately equal to the normal force multiplied by height.

Yo-Yo (Middling)

link title(Chabay)

Step 1: Solve for translational kinetic energy using the Point Particle System

(The equation for translational kinetic energy here is different than that in Point Particle Systems, so the derivation has been provided.)

Step Two: Solve for rotational kinetic energy using a Real System

Here is where the true difference between Real and Point Particle Systems can be seen. In the Point Particle system, there is no value to account for the change of rotational kinetic energy from the work done the hand. By changing the Work equation to 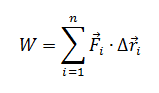rather than , the rotational kinetic energy can now be found.

Spring In a Box (Difficult)

Suppose a thin box contains a ball of clay with the mass M connected to a relaxed spring with a stiffness ks. The masses of the box and the spring are negligible. It is initally at rest, and then a constant force of F. The box moves a distance b and the spring stretches a distance s so that the clay sticks to the box. What is the change in thermal energy of the clay after colliding with the wall of the box?

From the analyzation of the Point Particle Systems of the Spring in a Box, we know that . Because the system is a spring, we also know that .

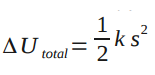
Assuming there is no relative kinetic energy (none based on diagram) and no change in chemical energy (there is no change in substance), the change in thermal energy of the clay can be found. Finding the change in thermal energy is important because you can determine whether there was enough energy to change the temperature of the clay or whether there is enough energy given off by the clay to change the temperature of a surrounding substance by a degree. Problems like this show the importance of analyzing real systems versus point particle systems.

Connectedness

How is this topic connected to something that you are interested in?

This topic interests me because from one single system you can mathematically determine the other forms of energy that can occur in various physical interaction. From the other forms of energy, you can determine whether there is enough energy to maybe change the temperature of another substance via thermal energy or even change the substance that is in the system given a big enough change in chemical energy.

How is it connected to your major?

As a chemical engineering major, the application of Real Systems is largely used for the majority of mathematics in my major dealing with energy balances. From only analyzing a system from a point particle method, one would only be able to find the change in the translational kinetic energy. In my major, it is very important to consider the entire system in order to find important values such as the change in thermal and kinetic energy because these values are often associated with the amount of work and heat produced in many chemical engineering processes.

Is there an interesting industrial application?

There is an absolute overload of interesting industrial applications for the analysis of real systems. In fact, the analysis of real systems in terms of energy balances is the entirety of what I've done in my chemical engineering classes thus far (I am currently a second year). There are many interesting (depending on your taste) uses of the real system analysis on a multitude of different turbines and chemical reactors.

External links

[1]

References

Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.

Wiki Commons Picture

--Nfortingo3(talk) 19:26, 28 November 2015 (EST)