Velocity: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
''Claimed by Stacey Nduati.'' | ''Claimed by Stacey Nduati.'' | ||
edited by Christian Sewall | |||
[[File:Whatisvelocity.gif|thumb|alt=Definition|What is velocity?]] | [[File:Whatisvelocity.gif|thumb|alt=Definition|What is velocity?]] | ||
Velocity is the | Velocity is the distance covered by an object in a specified direction over a time interval. In short, how fast something is moving, and what direction it is moving in. Velocity can be written as a vector, as it has both magnitude and direction. In contrast, speed only refers to how fast something is moving and has no direction. | ||
== | ==Main Idea== | ||
Velocity is the vector measure of the rate that the position of an object is changing divided by the time that change in position takes. This measure can be used in tandem with ideas such as The Momentum Principle to predict such values as position, momentum, and velocity after a specified time interval. | |||
== ==A Mathematical Model== == | |||
The primary way that velocity can be modeled is | |||
Average velocity can be calculated using the following equation: | Average velocity can be calculated using the following equation: | ||
:<math>\boldsymbol{\bar{v}} = \frac{\Delta\boldsymbol{r}}{\Delta\mathit{t}}</math> , | :<math>\boldsymbol{\bar{v}} = \frac{\Delta\boldsymbol{r}}{\Delta\mathit{t}}</math> , | ||
Revision as of 13:53, 27 November 2016
Claimed by Stacey Nduati. edited by Christian Sewall
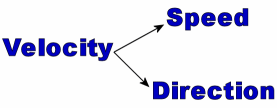
Velocity is the distance covered by an object in a specified direction over a time interval. In short, how fast something is moving, and what direction it is moving in. Velocity can be written as a vector, as it has both magnitude and direction. In contrast, speed only refers to how fast something is moving and has no direction.
Main Idea
Velocity is the vector measure of the rate that the position of an object is changing divided by the time that change in position takes. This measure can be used in tandem with ideas such as The Momentum Principle to predict such values as position, momentum, and velocity after a specified time interval.
==A Mathematical Model==
The primary way that velocity can be modeled is Average velocity can be calculated using the following equation:
- [math]\displaystyle{ \boldsymbol{\bar{v}} = \frac{\Delta\boldsymbol{r}}{\Delta\mathit{t}} }[/math] ,
where [math]\displaystyle{ {\Delta\boldsymbol{r}} }[/math] is the change of position of the object and [math]\displaystyle{ {\Delta\mathit{t}} }[/math] is the change of time.
The SI units for velocity are meters per second (m/s).
Example

A car takes 3 hours to make a 230-mile trip from Point A to Point B.
| Hour 1 | Hour 2 | Hour 3 | |
|---|---|---|---|
| Velocity | 80 mph north | 90 mph north | 60 mph north |
There are two kinds of velocity in which one must consider: instantaneous velocity and average velocity.
Instantaneous Velocity
Instantaneous velocity is the speed and direction of an object at a particular instant.
Given the example: Each hour has a different instantaneous velocity.
Average Velocity
Average velocity is the net displacement of an object, divided by the total travel time. It is the average of all instantaneous velocities. It is important to note that as [math]\displaystyle{ {\Delta\mathit{t}} }[/math] gets very small, the average velocity approaches the instantaneous velocity.
Given the example: The average velocity would be (230 miles/3 hours) = 76.67 mph north.
Acceleration
Acceleration is the time rate of change of velocity, with the following equation:
- [math]\displaystyle{ \boldsymbol{a} = \frac{\Delta\boldsymbol{v}}{\Delta\mathit{t}} }[/math] ,
where [math]\displaystyle{ {\Delta\boldsymbol{v}} }[/math] is the change of velocity of the object and [math]\displaystyle{ {\Delta\mathit{t}} }[/math] is the change of time.
The SI units for acceleration are meters per second per second (m/s/s). It is also a vector quantity.
Given the example: The acceleration from the 1st hour to the 2nd hour is 10 mph. This indicates a positive acceleration. The acceleration from the 2nd hour to the 3rd hour is -30 mph. This indicates a negative acceleration.
Connectedness
Velocity is a very interesting and important topic. Take into consideration pilots. flying an aircraft Pilots must combat strong winds while they are thousands of feet up in the air. It is not very useful for a pilot to know that the wind is traveling at 80 mph. What direction is it traveling in? The direction of this wind could prove to be useful, or to be a nightmare for the pilot! Pilots must know whether they are flying with the wind, or against the wind.
Also, take into consideration sports. In baseball, when the pitcher throws the ball to the batter, the batter must make a decision as to what he/she wants the ball's velocity to be. The ball can either go fast or slow (magnitude), or left or right (direction), etc. This immediate decision plays a huge role in how each team will increase their score during the game.
See Also
References
1. Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print.
2. "Velocity." Def. 2. Dictionary.com. N.p., n.d. Web. 29 Nov. 2015.
3. Velocity Expression. Digital image. Physics-Formulas. N.p., n.d. Web. 29 Nov. 2015.
4. Animated Car On Road. Digital image. Clip Art Best. N.p., n.d. Web. 29 Nov. 2015.