Friction

This page discusses the concept of friction and how it relates to both moving and static objects.

Claimed by drao31

The Main Idea

Friction is caused by the interactions between the atoms that make up objects. When objects interact, the atoms that make up the objects also interact. Temperatures of interacting surfaces rise because of such interactions. Friction is a force that resists movement. Generally, friction makes it harder to move objects. There are two main types of friction that are covered in Physics 2211: Static Friction and Kinetic Friction. Static friction can be described as the friction acting on resting objects. Kinetic friction is the friction acting on objects in motion.

Frictional forces depend on a few factors: the normal force and the coefficient of friction.

In simple terms, the normal force [math]\displaystyle{ {F}_{N} }[/math] or [math]\displaystyle{ {N} }[/math] is the equivalent force between objects. For example, when an object of mass M is placed on a table, there is a gravitational force Mg on the table. If the table can support the object without collapsing, the table exerts an equivalent force Mg on the object. According to the momentum principle, since there is no change in momentum, the net force must be 0. This is also apparent since there is no movement if the table can support the object.

[math]\displaystyle{ {p}_{f} - {p}_{i} = {F}_{net}{dt} = 0 }[/math]

OR

[math]\displaystyle{ {F}_{g} = {M}{g} }[/math]

[math]\displaystyle{ {N} = {M}{g} }[/math]

[math]\displaystyle{ {F}_{net} = {F}_{g} - {N} = {0} }[/math]

The coefficient of friction is usually specific to each object or material. The coefficient of static friction is denoted by [math]\displaystyle{ {μ}_{s} }[/math] and the coefficient of kinetic friction is denoted by [math]\displaystyle{ {μ}_{k} }[/math]

Static Friction:

[math]\displaystyle{ {F}_{s} \le {μ}_{s}{N} }[/math]

Static friction is the frictional force that must be overcome to begin moving an object at rest. The static friction can be no more than the normal force multiplied by the coefficient of static friction. Therefore, the maximum static friction an object can have is [math]\displaystyle{ {μ}_{s}{N} }[/math].

Kinetic Friction:

[math]\displaystyle{ {F}_{k} = {μ}_{k}{N} }[/math]

Kinetic friction is the frictional force that exists between objects already at motion. It acts to oppose the movement of an object. Kinetic friction can be observed, for example, when a soccer ball is kicked across a field. The friction between the ball and the field will eventually bring the ball to a stop.

Interestingly, friction is also required for rolling motion. Without friction, objects would not be able to roll. This is true because friction results in torque acting on the object, causing the rolling motion. An example of this can be seen in cars that are stuck in a ditch or similar situations. If there is not enough friction between the car's wheels and the ground, the car's wheels will simply spin in place, and the car will not move.

A Mathematical Model

As stated above:

Static Friction:

[math]\displaystyle{ {F}_{s} \le {μ}_{s}{N} }[/math]

Kinetic Friction:

[math]\displaystyle{ {F}_{k} = {μ}_{k}{N} }[/math]

When attempting to solve problems relating to friction, one possible method of approach is to consider the net force acting on an object. If there is a force [math]\displaystyle{ {F} }[/math] pushing an object to the right, and a frictional force [math]\displaystyle{ {F}_{f} }[/math] opposing the movement, then the net force is [math]\displaystyle{ {F}_{net} = {F} - {F}_{f} }[/math].

Another possible approach is by using the momentum principle [math]\displaystyle{ {p}_{f} - {p}_{i} = {F}_{net}{dt} }[/math]. The momentum principle can help solve problems where you need to account for time, net force, or change in momentum.

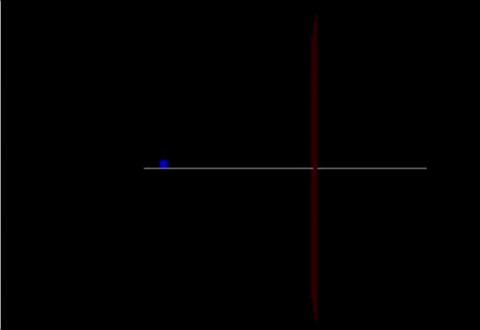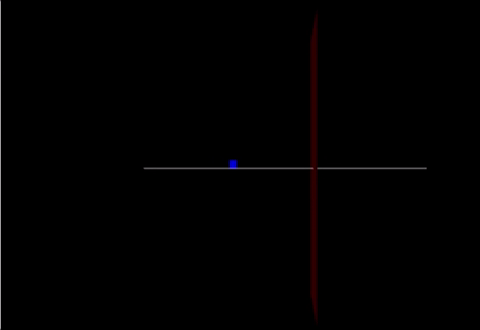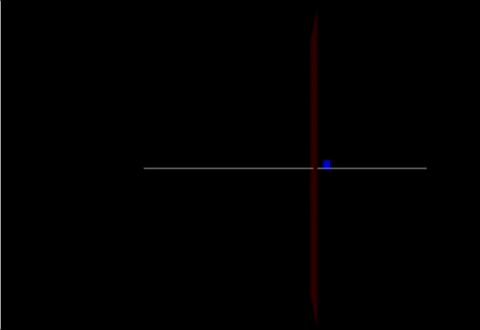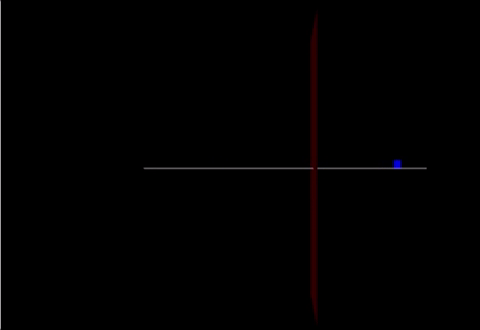
A Computational Model

Link: https://trinket.io/glowscript/76028c1809

Code:

def friction():
   from __future__ import division
   from visual import *
   from visual.graph import *

   mcart = 100
   mew = vector(2.9,0,0)

   track =  box(pos=vector(0,-0.05,0), size=vector(20.0,0.05,0.10), color=color.white)
   cart =  box(pos=vector(-10,0.25,0), size=vector(.5,0.6,0.03), color=color.blue)
   marker = box(pos = vector(2,0,0), size = vector(0,20,5), color = color.red)

   cart.v=vector(2.4,0,0)
   cart.p = mcart*cart.v
   F = vector(90,0,0)
   F2 = vector(-200,0,0)
   F3 = (mcart * mew)
   print(F3)

   deltat = 0.01
   t = 0

   while t < 5.02:

       if cart.pos.x < 2:
           cart.v = cart.p / cart.m
           Fnet = F
           cart.p = cart.p + Fnet*deltat
           cart.pos = cart.pos + (cart.p/mcart)*deltat

       else:
           
           cart.v = cart.p / cart.m
           Fnet = F-F3
           cart.p = cart.p + Fnet*deltat
           cart.pos = cart.pos + (cart.p/mcart)*deltat
           
       t = t + deltat
       rate(100)
       
   print(cart.pos)
   
friction()

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

A 100Kg box is placed on a flat table. The box does not move. The coefficient of static friction [math]\displaystyle{ {μ}_{s} = {.25} }[/math] and the coefficient of kinetic friction [math]\displaystyle{ {μ}_{k} = {.15} }[/math]. Find the force of friction [math]\displaystyle{ {F}_{s} }[/math].

Solution:

Since the box does not move, there is only static friction. The normal force is equivalent to the force due to gravity: [math]\displaystyle{ {F}_{N} = {F}_{g} = {100}{g} }[/math]. The static friction can be found by: [math]\displaystyle{ {F}_{s} = {μ}_{s}{F}_{N} }[/math]

[math]\displaystyle{ {F}_{s} = {(.25)}{(100)}{(9.8)} = {245.25} }[/math]

Middling

A cart of mass 3Kg moves across a track pushed by a fan which exerts [math]\displaystyle{ {F} = \lt 3,0,1\gt }[/math]N with an initial velocity [math]\displaystyle{ {v}_{i} = \lt 1,0,1\gt \frac{{m}}{{s}} }[/math] . Find the required coefficient of kinetic friction [math]\displaystyle{ {μ}_{k} }[/math] needed to bring the cart to a stop in 10 seconds.

Solution:

Use the momentum principle: [math]\displaystyle{ {p}_{f} - {p}_{i} = {F}_{net}{dt} }[/math] and [math]\displaystyle{ {F}_{f} = {μ}_{k}{N} }[/math]

The final velocity must be 0. The initial velocity, initial force, and time are given.

[math]\displaystyle{ 0- \lt 3,0,3\gt = {F}_{net}{10s} }[/math]

[math]\displaystyle{ {F}_{net} = \lt -0.3,0,-0.3\gt }[/math]

[math]\displaystyle{ \lt -0.3,0,-0.3\gt = \lt 3,0,1\gt - {F}_{f} }[/math]

[math]\displaystyle{ {F}_{f} = \lt 3.3,0,1.3\gt }[/math]

[math]\displaystyle{ {F}_{f} = \lt 3.3,0,1.3\gt = {μ}_{k}{N} }[/math]

[math]\displaystyle{ {N} = {3Kg} * {0,9.8,0} }[/math]

[math]\displaystyle{ {μ}_{k} = \frac{{F}_{f}}{{N}} = \frac{{\lt 3.3,0,1.3\gt }}{{0,29.43,0}} }[/math]

Difficult

Two blocks are stacked on top of one another on a frictio

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page