Energy Transfer due to a Temperature Difference

This section will be sharing how to calculate energy transfer in systems that are affected by temperature changes. This related to Chapter 7 in the Text Book and Exam 3.

Woong Jun Park
wpark39

Carter Gillon (cgillon3), Fall 2016

The Main Idea

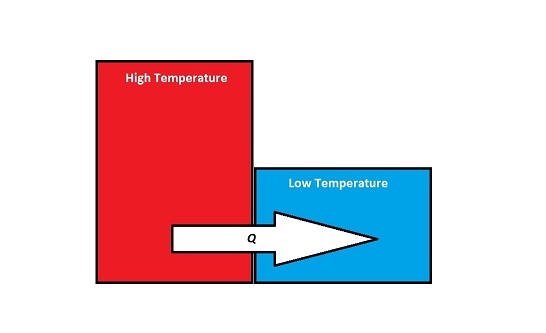
When two objects that have different temperatures come into contact with one another, energy will be transferred from the object with the higher temperature to the object with the lower temperature. Although work is occurring at a microscopic level, since at the point of contact, the individual atoms on the surfaces of the objects are doing work on each other, this energy transfer is not referred to as work, W, because there are no macroscopic forces or displacements. Instead:

Energy Transfer Due to a Temperature Difference = [math]\displaystyle{ Q }[/math]

Therefore, for an open system, the energy principle is:

[math]\displaystyle{ ∆E_{system} = Q + W + }[/math] other energy transfers

• Q is used to describe the amount of energy that is exchanged between the system and surroundings when there is a temperature difference between them (microscopic work)
• W is used to describe the energy transfer due to other forces (macroscopic, mechanical work)
• other energy transfers could include matter transfer, mechanical waves, electricity, electromagnetic radiation, etc...

Sign of Q

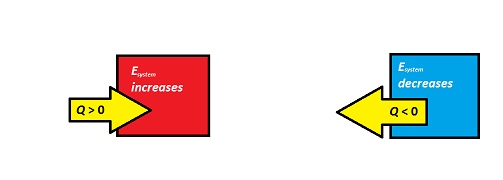
[math]\displaystyle{ Q }[/math] can be positive or negative depending on the energy change.

If energy is transferred from the system to the surroundings (the system is getting colder), then [math]\displaystyle{ Q }[/math] is negative. If energy is transferred from the surroundings to the system (the system is heating up), then [math]\displaystyle{ Q }[/math] is positive.

The Steady State When a system is described as being in "steady state", that means that the overall energy of the system, [math]\displaystyle{ E_{system} }[/math], does not change despite the other energy transfers occurring in the system. Also, for a system to be at steady state, the energy flow flowing into the system must be doing so at the same rate as the energy flowing out of the system.

A Mathematical Model

The following are mathematical models that you will use in these calculations:

The Energy Principle

• [math]\displaystyle{ ∆E_{system} = Q + W + }[/math] other energy transfers

Calculating Heat Transfer

• [math]\displaystyle{ ∆E_{thermal} = mC(∆T) }[/math]

[math]\displaystyle{ ∆E_{thermal} }[/math] = Heat Added

[math]\displaystyle{ m }[/math] = mass

[math]\displaystyle{ C }[/math] = Specific Heat

[math]\displaystyle{ ∆T }[/math] = change in Temperature

Calculating the Temperatures of Two Objects in Contact

• [math]\displaystyle{ ∆E_{system} = Q + W + }[/math] other energy transfers

[math]\displaystyle{ W = 0 }[/math], other = 0, so [math]\displaystyle{ ∆E_{system} = Q = 0 }[/math]

• [math]\displaystyle{ ∆E_{system} = 0 = ∆E_{thermal,1} +∆E_{thermal,2} }[/math]
• [math]\displaystyle{ 0 = mC_1(T_f - T_1) + mC_2(T_f - T_2) }[/math]

A Computational Model

Check this video out for a brief understanding of how Heat & Temperature relate to Physics.
Heat Transfer

Check this video out for a detailed look into the topic.
Relationship between deltaE and Q+W

Examples

Middling

You put a thin metal pot containing 3787 [math]\displaystyle{ g }[/math] of room-temperature (20 °C) water on a hot electric stove. You also stir the water vigorously with an electric beater, which does 100 [math]\displaystyle{ J }[/math] of work on the water every second. You observe that after 10 minutes the water starts to boil (100 °C). The specific heat capacity of water is 4.2 [math]\displaystyle{ J(g·C)^{−1} }[/math]. What is the thermal transfer of energy, [math]\displaystyle{ Q }[/math], into the water from the surroundings?

Solution:

[math]\displaystyle{ ∆E_{system} = W_{surr} + Q }[/math]

[math]\displaystyle{ ∆E_{thermal} = W_{surr} + Q }[/math]

[math]\displaystyle{ Q = ∆E_{thermal} - W_{surr} }[/math]

[math]\displaystyle{ ∆E_{thermal} = mC(∆T) = (3787 g)(4.2 J(g·C)^{−1})(100 - 20 °C) }[/math]

[math]\displaystyle{ ∆E_{thermal} = 1.272 }[/math] x [math]\displaystyle{ 10^6 J }[/math]

[math]\displaystyle{ W_{surr} = W*t = (100 J*s^{-1})(10 * 60s) }[/math]

[math]\displaystyle{ W_{surr} = 6 }[/math] x [math]\displaystyle{ 10^4 J }[/math]

[math]\displaystyle{ Q = ∆E_{thermal} - W_{surr} = 1.272 }[/math] x [math]\displaystyle{ 10^6 J - 6 }[/math] x [math]\displaystyle{ 10^4 J }[/math]

[math]\displaystyle{ Q = 1.212 }[/math] x [math]\displaystyle{ 10^6 J }[/math]

Difficult

You have two cups of coffee. Each cup contains 350 grams of coffee at 93 °C. The specific heat of coffee is 4.2 [math]\displaystyle{ J(g·°C)^{−1} }[/math]. Assume that no energy is transferred between the coffee and the cup.

• A. If you want to bring the coffee down to a temperature of 82 °C, how much cream do you have to add if the cream's initial temperature is 5 °C and it has a specific heat of 3.8 [math]\displaystyle{ J(g·°C)^{−1} }[/math]?

Solution:

1 = the cup of coffee

2 = the cream

need to find the mass of the cream you need to add:

[math]\displaystyle{ ∆E = ∆E_{thermal, 1} + ∆E{thermal, 2} }[/math]

[math]\displaystyle{ m_1C_1(T_f - T_1) + m_2C_2(T_f - T_2) = 0 }[/math]

[math]\displaystyle{ m_2C_2(T_f - T_2) = -m_1C_1(T_f - T_1) }[/math]

[math]\displaystyle{ m_2 = -m_1C_1(T_f - T_1)/C_2(T_f - T_2) = (350 g)(4.2 J(g·°C)^{−1})(82°C - 93 °C) / (3.8(g·°C)^{−1})(882°C - 5 °C) }[/math]

[math]\displaystyle{ m_2 = 55.3 g }[/math]

Connectedness

I am a Business, Pre-Dental student so health topics have always been very interesting to me. Although this topic may not relate directly to my major, it does have real world applications in the health field.

Specific heat and this transfer of energy can be applied to taking patient's temperatures using a thermometer. There is liquid and material that is inside the thermometer that a have low specific capacities. This allows for a very precise measurement of the temperature. This is not necessarily

Another industrial application can e seen in engine parts that expand and contract because of the constant change in heat within the engine.

History

The history of heat and work can be dated back to 1789 when the French scientist Antoine Lavoisier created a new theory - the phlogiston theory on Chemistry that basically negated all previous findings of combustion. He gave heat a meaning and definition that led to the interpretation of heat that is accepted today.

The modern interpretation is what we hold true in the example questions that we used earlier Q = mCdeltatT.

In 1798, Benjamin Thompson - minister for war and police in the German state of Bavaria - wanted to figure out where all the heat from the cannons were coming from. He observed that the surroundings of the cannon got hotter and not colder. He hypothesized that some of the mechanical work done on the cannon was converted to heat.

In 1849, English physicist James Prescott Joule published his work and findings on the conversion of work to heat that Thompson started. He formulated work equivalent of heat. 1 newton meter of work = 0.241 calories of heat.

In 1850, German physicist Clausius published his works on how conserved quantity is neither heat nor work, but a combination of both. He named this Energy and that is where we get the macroscopic equation deltaE = Q - W.

See also

Relevant material and additional reading can be looked into the history of Joule and the laws of thermodynamics.

Further reading

Specific Heat: Britannica
Dependence of Heat Capacity on Thermal History: Nature Publishing Group
Environmental Research Web | Uneven Climate Change Due to Atmospheric Heat Capacity

External links

USGS Water Science School
Science Direct | Determination of specific heat capacity by transient plane source
Heat Transfer
Relationship between deltaE and Q+W

References

"A Brief History of Heat and Work." A Brief History of Heat and Work. N.p., n.d. Web. 10 Nov. 2015.\

"Application of Specific Heat Capacity" : Application of Specific Heat Capacity. N.p., n.d. Web. 10 Nov. 2015.

"CHAPTER 4: HEAT." : 4.2 Specific Heat Capacity. N.p., n.d. Web. 10 Nov. 2015.

Division of Building Technology, Chalmers University of Technology, Gothenburg SE-412 96, Sweden Received 23 August 2013, Revised 3 September 2013, Accepted 10 September 2013, Available online 22 October 2013

"Re: What Are Some Practical Uses of Determining the Specific Heat of a Metal?" Re: What Are Some Practical Uses of Determining the Specific Heat of a Metal? N.p., n.d. Web. 10 Nov. 2015.