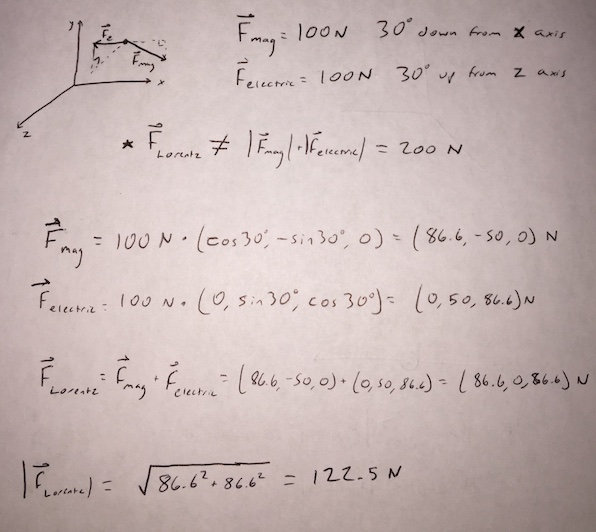Lorentz Force: Difference between revisions
Chrismickas (talk | contribs) |
Chrismickas (talk | contribs) |
||
| Line 50: | Line 50: | ||
==History== | ==History== | ||
[[File:hlorentz.jpg|200px|thumb|right|Hendrik Lorentz]] | [[File:hlorentz.jpg|200px|thumb|right|Hendrik Lorentz]] | ||
The | The Lorentz Force is named after Hendrik Lorentz, who derived the formula in the late 19th century following a previous derivation by [[Oliver Heaviside]] in 1889. However, scientists had tried to find formulas for one electromagnetic force for over a hundred years before.Some scientists such as [[Henry Cavendish]] argued that the magnetic poles of an object could create an electric force on a particle that obeys an inverse-square law. However, the experimental proof was not enough to definitively publish. In 1784, [[Charles de Coulomb]], using a torsion balance, was able to definitively show through experiment that this was true. After [[Hans Christian Ørsted]] discovered that a magnetic needle is acted on by a voltaic current, [[Andre Marie Ampere]] derived a new formula for the angular dependence of the force between two current elements. However, the force was still given in terms of the properties of the objects involved and the distances between, not in terms of electric and magnetic fields or forces. | ||
[[Michael Faraday]] introduced modern ideas of magnetic and electric fields, including their interactions and relations with each other, later to be given full mathematical description by [[William Thomson (Lord Kelvin)]] and [[James Maxwell]]. From a modern perspective it is possible to identify in Maxwell's 1865 formulation of his field equations a form of the Lorentz force equation in relation to electric currents, however, it was not initially evident how his equations related to the forces on moving charged objects. [[J.J. Thomson]] was the first to attempt to derive from Maxwell's field equations the electromagnetic forces on a moving charged object in terms of the object's properties and external fields. Interested in determining the electromagnetic behavior of the charged particles in cathode rays, Thomson published a paper in 1881 wherein he gave the force on the particles due to an external magnetic field as <math>\vec{F} = q\vec{E} + \frac{q}{2}\vec{v} ⨯ \vec{B}</math>. Finally, Heaviside and later Lorentz were able to combine the information into the currently accepted Lorentz Force equation. | |||
== See also == | == See also == | ||
Revision as of 20:31, 27 November 2016
Claimed by Chris Mickas 11/15/16
The Main Idea
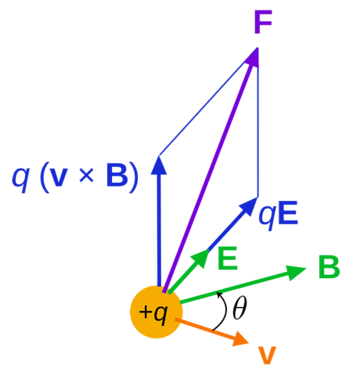
The Lorentz Force is a name for the sum of the magnetic and electric forces on a particle. The net force on some particles is often primarily determined by the electric and magnetic forces because other forces are negligible. In these cases, the Lorentz Force refers to the net force found by adding the magnetic and electric forces.
A Mathematical Model
[math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} }[/math] where [math]\displaystyle{ q\vec{E} }[/math] is the electric force and [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math] is the magnetic force.
A Computational Model
Examples
Simple
If the electric force points in the +x direction and the magnetic force points in the –x direction, what direction does the Lorentz force point in?

Solution: More information is needed to know the direction of the force.
Middling
The electric force on a certain particle is <100,-600,300> N and the magnetic force is <-600,400,0> N. Find the Lorentz force.

Solution: Lorentz force = <-500,-200,300> N
Difficult
The magnetic force on a proton is 100 N 30 degrees down from the +x direction. The electric force on the same proton is 100 N 30 degrees up from the +z direction. What is the magnitude of the Lorentz Force on the proton?
Solution: Lorentz force = 122.5 N
Connectedness
1. I'm very interested in music and sound amplification. Speakers use the Lorentz force of an electromagnet to move a cone that creates sound waves in the air. When current flows through the wires in the electromagnetic in different quantities, the speakers move in unique ways to produce the different sounds that we recognize. Amplifiers for electric guitars and basses work in the same way. As a guitar player, I'm interested by the physics of how electric guitars work.
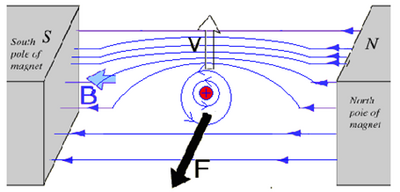
2. One of my areas of interest as a mechanical engineering student is sustainable and renewable energy. Wind turbines and hydropower plants both work by harnessing the kinetic energy of water or wind and using it to induce an electrical current. The turbines rotate and move a permanent magnet that induces a current in an electromagnet placed inside of the magnet, which is shaped like a hollow cylinder. The induced current is then carried via wires to external sources to provide energy.
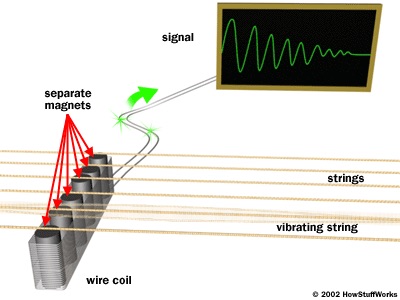
3. Several industries manufacture products that induce current using the Lorentz Force. For example, electric guitars and basses work by magnetizing the strings and relying on the Lorentz force to create a current in pickups that is then transmitted to an amplifier. Pickups are small electromagnet coils surrounding a magnet that are placed beneath the strings. The strings become magnetized because of the magnet inside the pickup. When they are played and vibrate, they induce current in the electromagnet. The Lorentz force causes the strings to exert forces that move mobile charges and induce the current. The current is then increased through a potentiometer and sent to an amplifier through a cable.
History

The Lorentz Force is named after Hendrik Lorentz, who derived the formula in the late 19th century following a previous derivation by Oliver Heaviside in 1889. However, scientists had tried to find formulas for one electromagnetic force for over a hundred years before.Some scientists such as Henry Cavendish argued that the magnetic poles of an object could create an electric force on a particle that obeys an inverse-square law. However, the experimental proof was not enough to definitively publish. In 1784, Charles de Coulomb, using a torsion balance, was able to definitively show through experiment that this was true. After Hans Christian Ørsted discovered that a magnetic needle is acted on by a voltaic current, Andre Marie Ampere derived a new formula for the angular dependence of the force between two current elements. However, the force was still given in terms of the properties of the objects involved and the distances between, not in terms of electric and magnetic fields or forces.
Michael Faraday introduced modern ideas of magnetic and electric fields, including their interactions and relations with each other, later to be given full mathematical description by William Thomson (Lord Kelvin) and James Maxwell. From a modern perspective it is possible to identify in Maxwell's 1865 formulation of his field equations a form of the Lorentz force equation in relation to electric currents, however, it was not initially evident how his equations related to the forces on moving charged objects. J.J. Thomson was the first to attempt to derive from Maxwell's field equations the electromagnetic forces on a moving charged object in terms of the object's properties and external fields. Interested in determining the electromagnetic behavior of the charged particles in cathode rays, Thomson published a paper in 1881 wherein he gave the force on the particles due to an external magnetic field as [math]\displaystyle{ \vec{F} = q\vec{E} + \frac{q}{2}\vec{v} ⨯ \vec{B} }[/math]. Finally, Heaviside and later Lorentz were able to combine the information into the currently accepted Lorentz Force equation.
See also
The Hall Effect is a special case in which the magnetic and electric forces on a particle or object cancel out, meaning that there is zero net force. Solving these problems involves setting the two forces equal to each other and using given information to find values for [math]\displaystyle{ \vec{B} }[/math], [math]\displaystyle{ \vec{v} }[/math], or [math]\displaystyle{ \vec{E} }[/math].

If you wish to further explore how electricity and magnetism interact via the Lorentz force, watch this video that provides interesting real-life examples!
Further reading
- http://hyperphysics.phy-astr.gsu.edu/HBASE/hframe.html
- http://www.ittc.ku.edu/~jstiles/220/handouts/section%203_6%20The%20Lorentz%20Force%20Law%20package.pdf
External links
- http://jnaudin.free.fr/lifters/lorentz/
- https://nationalmaglab.org/education/magnet-academy/watch-play/interactive/lorentz-force
References
- Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew L. (2006). The Feynman lectures on physics (3 vol.). Pearson / Addison-Wesley. ISBN 0-8053-9047-2.: volume 2.
- Jackson, John David (1999). Classical electrodynamics (3rd ed.). New York, [NY.]: Wiley. ISBN 0-471-30932-X.
- Serway, Raymond A.; Jewett, John W., Jr. (2004). Physics for scientists and engineers, with modern physics. Belmont, [CA.]: Thomson Brooks/Cole. ISBN 0-534-40846-X.