Faraday's Law

in progress by hannah blankenship fall 2017

Faraday's Law focuses on how a time-varying magnetic field produces a "curly" non-Coulomb electric field, thereby inducing an emf.

Faraday's Law

Faraday's Law summarizes the ways voltage can be generated as a result of a time-varying magnetic flux. It helps connect magnetic field and electric field in a quantifiable way. Faraday's law is one of four laws in Maxwell's equations. It tells us that in the presence of a time-varying magnetic field or current (which induces a time-varying magnetic field), there is an emf with a magnitude equal to the change in magnetic flux. It serves as a succinct summary of the ways a voltage (or emf) may be generated by a changing magnetic environment. The induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil. It involves the interaction of charge with magnetic field.

Curly Electric Field

Faraday's Law Experiment

Faraday showed that no current is registered in the galvanometer when bar magnet is stationary with respect to the loop. However, a current is induced in the loop when a relative motion exists between the bar magnet and the loop. In particular, the galvanometer deflects in one direction as the magnet approaches the loop, and the opposite direction as it moves away.

Faraday’s experiment demonstrates that an electric current is induced in the loop by changing the magnetic field. The coil behaves as if it were connected to an emf source. Experimentally it is found that the induced emf depends on the rate of change of magnetic flux through the coil.

Test it out yourself here

Mathematical Model

Faraday's Law

emf = [math]\displaystyle{ {\frac{-d{{Φ}}_{mag}}{dt}} }[/math]

where emf = [math]\displaystyle{ \oint\vec{E}_{NC}\bullet d\vec{l} }[/math] and [math]\displaystyle{ {{Φ}}_{mag}\equiv\int\vec{B}\bullet\hat{n}dA }[/math]

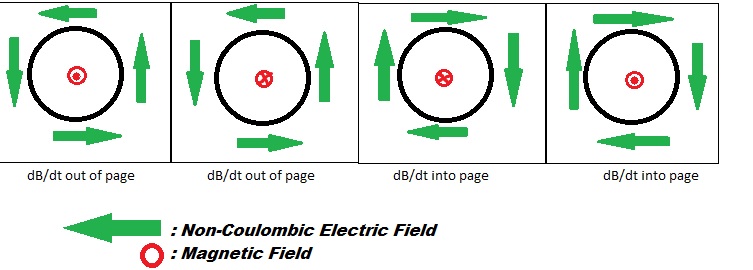
In other words: The emf along a round-trip is equal to the rate of change of the magnetic flux on the area encircled by the path.

Direction: With the thumb of your right hand pointing in the direction of the -dB/dt, your fingers curl around in the direction of Enc.

The meaning of the minus sign: If the thumb of your right hand points in the direction of -dB/dt (that is, the opposite of the direction in which the magnetic field is increasing), your fingers curl around in the direction along which the path integral of electric field is positive. Similarly, the direction of the induced current can be explained using Lenz's Law. Lenz's law states that the induced current from the non-Coulombic electric field is induced in such a way that it produces a magnetic field that opposes the first magnetic field to keep the magnetic flux constant.

Formal Version of Faraday's Law

[math]\displaystyle{ \oint\vec{E}_{NC}\bullet d\vec{l} = {\frac{-d}{dt}}\int\vec{B}\bullet\hat{n}dA }[/math] (sign given by right-hand rule)

Problem Solving Tips

To find the direction of the curly electric field, one must find the direction of [math]\displaystyle{ \frac{-dB}{dt} }[/math]. Do this using the change in magnetic field as the basis of finding the [math]\displaystyle{ \frac{-dB}{dt} }[/math].

The easiest way to do this is to imagine the a vector for the initial magnetic field, and a vector for the final magnetic field. Then, draw the change in magnetic field vector, [math]\displaystyle{ \Delta \mathbf{B} }[/math], and then the negative vector of that change in magnetic field gives [math]\displaystyle{ \frac{-dB}{dt} }[/math]:

Pointing the thumb of your right hand in the direction of [math]\displaystyle{ \frac{-dB}{dt} }[/math] allows you to curl your fingers in the direction of [math]\displaystyle{ \mathbf{E_{NC}} }[/math].

In this chapter we have seen that a changing magnetic flux induces an emf:

according to Faraday’s law of induction. For a conductor which forms a closed loop, the emf sets up an induced current I =|ε|/R , where R is the resistance of the loop. To compute the induced current and its direction, we follow the procedure below:

1. For the closed loop of area on a plane, define an area vector A and let it point in the direction of your thumb, for the convenience of applying the right-hand rule later. Compute the magnetic flux through the loop using

Determine the sign of the magnetic flux

2. Evaluate the rate of change of magnetic flux . Keep in mind that the change could be caused by

Determine the sign of

3. The sign of the induced emf is the opposite of that of . The direction of the induced current can be found by using Lenz’s law or right hand rule (discussed previously).

More on Faraday's Law

Moving a magnet near a coil is not the only way to induce an emf in the coil. Another way to induce emf in a coil is to bring another coil with a steady current near the first coil, thereby changing the magnetic field (and flux) surrounding the first coil, inducing an emf and a current. Also, rotating a bar magnet (or coil) near a coil produces a time-varying magnetic field in the coil since rotating the magnet changes the magnetic field in the coil. The key to inducing the emf in the second coil is to change the magnetic field around it somehow, either by bringing an object that has its own magnetic field around that coil, or changing the current in that object, changing its magnetic field.

Faraday's law can be used to calculate motional emf as well. A bar on two current-carrying rails connected by a resistor moves along the rails, using magnetic force to induce a current in the wire. There is a magnetic field going into the page. One way to calculate the motional emf is to use the magnetic force, but an easier way is to use Faraday's law.

Faraday's law, using the change in magnetic flux, can be used to find the motional emf, where the changing factor in the magnetic flux is the area of the circuit as the bar moves, while magnetic field is kept constant.

Examples

Simple

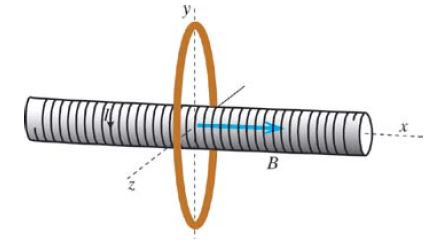
Adapted from the Matter & Interactions textbook, variation of P12 (4th ed).

The solenoid radius is 4 cm and the ring radius is 20 cm. B = 0.8 T inside the solenoid and approximately 0 outside the solenoid. What is the magnetic flux through the outer ring?

Solution:

Because the magnetic field outside the solenoid is 0, there is no flux between the ring and solenoid. So the flux in the ring is due to the area of the solenoid, so we use the area of the solenoid to find the flux through the outer ring rather than the area of the ring itself:

[math]\displaystyle{ \phi = BAcos(\theta) }[/math]

[math]\displaystyle{ = (0.8 T)(\pi)(0.04 m)^2cos(0) }[/math]

[math]\displaystyle{ = 4.02 x 10^{-3} T*m^2 }[/math]

Middle

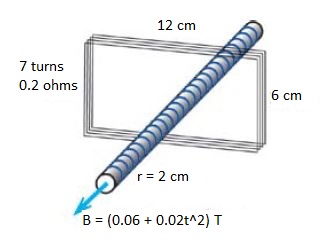
Adapted from the Matter & Interactions textbook, variation of P27 (4th ed).

A very long, tightly wound solenoid has a circular cross section of radius 2 cm (only a portion of the very long solenoid is shown). The magnetic field outside the solenoid is negligible. Throughout the inside of the solenoid the magnetic field B is uniform, to the left as shown, but varying with time t: B = (.06+.02[math]\displaystyle{ t^2 }[/math])T. Surrounding the circular solenoid is a loop of 7 turns of wire in the shape of a rectangle 6 cm by 12 cm. The total resistance of the 7-turn loop is 0.2 ohms.

(a) At t = 2 s, what is the direction of the current in the 7-turn loop? Explain briefly.

(b) At t = 2 s, what is the magnitude of the current in the 7-turn loop? Explain briefly.

Solution

(a) The direction of the current in the loop is clockwise.

(b)

B(t) = (.06+.02[math]\displaystyle{ t^2 }[/math])

A = (.12 m)(.06 m) = .0072 [math]\displaystyle{ m^2 }[/math]

[math]\displaystyle{ |{ε}| = AN\frac{dB(t)}{dt} }[/math]

[math]\displaystyle{ |{ε}| }[/math] = (.0072 [math]\displaystyle{ m^2 }[/math])(7)[math]\displaystyle{ \frac{d(.06+.02t^2)}{dt} }[/math] = (.0504)(.02)(2t) = .002016t

At t = 2 s:

[math]\displaystyle{ |{ε}| }[/math] = .002016(2) = .004032 V

[math]\displaystyle{ i = \frac{{ε}}{R} }[/math]

[math]\displaystyle{ i = \frac{{.004032 V}}{0.2 ohms} }[/math] = .02016 A

Conceptual Question

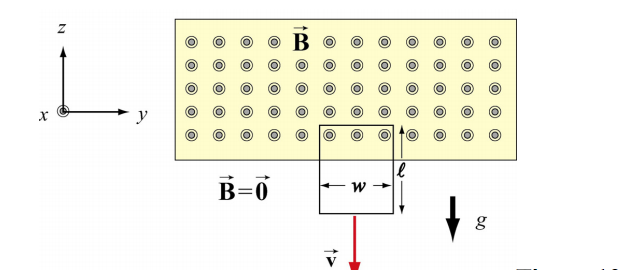
Falling Loop

A rectangular loop of wire with mass m, width w, vertical length l, and resistance R falls out of a magnetic field under the influence of gravity. The magnetic field is uniform and out of the paper within the area shown and zero outside of that area. At the time shown in the sketch, the loop is exiting the magnetic field at speed

1) What is the direction of the current flowing in the circuit at the time shown, clockwise or counterclockwise? Why did you pick this direction?

2) Using Faraday's law, find an expression for the magnitude of the emf in this circuit in terms of the quantities given. What is the magnitude of the current flowing in the circuit at the time shown?

3) Besides gravity, what other force acts on the loop in the ±k direction? Give its magnitude and direction in terms of the quantities given.

4) Assume that the loop has reached a “terminal velocity” and is no longer accelerating. What is the magnitude of that terminal velocity in terms of given quantities?

5) Show that at terminal velocity, the rate at which gravity is doing work on the loop is equal to the rate at which energy is being dissipated in the loop through Joule heating.

Connectedness

Faraday's Law is one of Maxwell's equations which describe the essence of electric and magnetic fields. Maxwell's equations effectively summarize and connect all that we have learned over the course of Physics 2.