Magnetic Field of a Solenoid Using Ampere's Law

Claimed by Mary Jane Chandler Fall 2016

This page explains how to use Ampere's Law to solve for the magnetic field of a solenoid.

The Main Idea

A solenoid is a cylindrical coil of wire that produces a uniform magnetic field when it is carrying an electric current. A solenoid is a form of an electromagnet that can create strong controlled magnetic fields throughout the coil except at the ends. Ampere's Law states that the magnetic field in space around an electric current is proportional to the source of the electric current. This can be applied to solve the magnetic field of a Solenoid.

As you can see in this model, in the middle of the solenoid the field is constant throughout the entirety of the interior and is parallel to the axis. At the ends of a solenoid the magnetic field starts to point outward at varying angles.

Equation

If there are [math]\displaystyle{ N }[/math] loops of wire that compose a solenoid of length [math]\displaystyle{ L }[/math], and we know that Ampere's Law gives us the form:

[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside path}} }[/math]

We can then solve for [math]\displaystyle{ B }[/math]:

[math]\displaystyle{ {B = \frac{μ_{0}NI}{L}} }[/math]

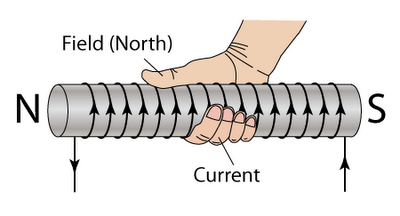
The Right Hand Rule can be used to find the direction of the magnetic field by using your right hand and curling your fingers in the direction of the current with your thumb pointing in the direction of the magnetic field. This is always along the axis for a solenoid.

Examples

Solving for the Magnetic Field

Find the magnetic field produced by a 20 cm long solenoid if the number of loops is 200 and current passing through it is 8 A.

For this example all of the variables are given so it is just a simple math calculation using Ampere's Law, as given above, but for reiteration.

[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside path}} }[/math]

[math]\displaystyle{ {B = \frac{200*8}{.2}} }[/math] [math]\displaystyle{ {B = 8,000} }[/math]

Once you have solved for [math]\displaystyle{ B }[/math] all you have to do is find the direction of the magnetic field using the Right Hand Rule.

• Must convert 20 cm to .2 m

Solving for the Current

A solenoid has a magnetic field of 6x10^-4 T, 2000 turns, and is 10 cm long. What is the current through the solenoid? For this example you are solving for I. Very similar to the above question, just rearranging the calculation of Ampere's Law.

[math]\displaystyle{ {I = \frac{LB}{μ_{0}N}} }[/math]

[math]\displaystyle{ {I = \frac{.1*6E-4}{2000}} }[/math] [math]\displaystyle{ {I = 3E-8 A} }[/math]

• Must change 10 cm to .1 for the cm to m conversion

Connectedness

1. Solenoids are important because they can create controlled magnetic fields making them useful for a variety of applications
2. As a Biology major this relates to my major because solenoids are very important in the medical field. An example of solenoids is that they are very beneficial when it comes to controlling the flow of medicine that enters the bloodstream of individuals.

See Also

Ampere's Law

Magnetic Field of a Long Thick Wire Using Ampere's Law

Magnetic Field of Coaxial Cable Using Ampere's Law

Magnetic Field of a Toroid Using Ampere's Law

Further Reading

Chabay, Sherwood. (2015). Matter and Interactions (4th ed., Vol. 2). Raleigh, North Carolina: Wiley.

External Links

• http://www.physicstutorials.org/home/magnetism/magnetic-field-around-a-solenoid

• http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/solenoid.html

References

Chabay, Sherwood. (2015). Matter and Interactions (4th ed., Vol. 2). Raleigh, North Carolina: Wiley. Pg 887-888.