Electric Field and Electric Potential: Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
'''Claimed by Terrence Connors''' | '''Claimed by Terrence Connors''' | ||
'''Edited by Frederick Erebor''' | |||
==The Main Idea== | ==The Main Idea== | ||
In physics, many phenomena that we observe are interrelated in some capacity. In the study of electricity and magnetism, several important physical quantities that play a crucial role in understanding physical interactions are derived from one another. Electric Field is a concept that is discussed early in most Electricity and Magnetism curricula, but it has enormous impact once we discover that it tells us information about Electric Potential, and from that, Potential Energy. This helps physicists to understand both the mechanics of a system | In physics, many phenomena that we observe are interrelated in some capacity. In the study of electricity and magnetism, several important physical quantities that play a crucial role in understanding physical interactions are derived from one another. Electric Field is a concept that is discussed early in most Electricity and Magnetism curricula, but it has an enormous impact once we discover that it tells us information about Electric Potential, and from that, Potential Energy. This helps physicists to understand both the mechanics of a system and the quantized nature of a system. | ||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
| Line 13: | Line 15: | ||
If we think back to the study of conservation of energy, we know that the change in potential energy of a system is work, which is a force being applied over a distance. Since force and distance are vectors, integrating up over the distance of applied force, we obtain: | If we think back to the study of conservation of energy, we know that the change in potential energy of a system is work, which is a force being applied over a distance. Since force and distance are vectors, integrating up over the distance of applied force, we obtain: | ||
<math>{\Delta U=-\int_i^f {\vec{F} • \vec{ds}}}</math>. By analogy, we define the electric potential as the energy per coulomb | <math>{\Delta U=-\int_i^f {\vec{F} • \vec{ds}}}</math>. By analogy, we define the electric potential as the energy per coulomb or potential energy divided by charge: | ||
<math>{\Delta V=-\int_i^f {\vec{E} • \vec{ds}}}</math>. | <math>{\Delta V=-\int_i^f {\vec{E} • \vec{ds}}}</math>. | ||
| Line 21: | Line 23: | ||
We can model how a system will change in electric potential and potential energy as we move, for example, through a uniform electric field in programs like VPython. One could visualize the electric field, electric force, and quantitatively determine the potential and potential energy as, for instance, a system as simple as a single particle moves through space. | We can model how a system will change in electric potential and potential energy as we move, for example, through a uniform electric field in programs like VPython. One could visualize the electric field, electric force, and quantitatively determine the potential and potential energy as, for instance, a system as simple as a single particle moves through space. | ||
[[File:Bamf.png]] | |||
==Examples== | ==Examples== | ||
| Line 64: | Line 67: | ||
==Connectedness== | ==Connectedness== | ||
The topic of | The topic of Electric field and electric potential is particularly interesting because it gives scientists and physicists in particular so much insight into the systems they are studying. If we can model the electric field and thus the electric force that an object feels, we gain such a more in-depth understanding of the underlying mechanics of the system, thus enabling us to better model the motion of the system, and understand the energy that the system gains or loses. I think this is incredibly interesting. | ||
There are not many direct impacts of the discussion of electric field and electric potential in the study of Chemical Engineering, but in the study of Chemical Engineering Thermodynamics, this does directly affect chemical potential. Chemical potential is a form of potential energy associated with phase change and chemical reaction. At equilibrium, the chemical potential of a system is zero. The definition of chemical potential is incredibly important in the study of thermodynamics, particularly when analyzing the Gibbs Free Energy of a system. | There are not many direct impacts of the discussion of electric field and electric potential in the study of Chemical Engineering, but in the study of Chemical Engineering Thermodynamics, this does directly affect chemical potential. Chemical potential is a form of potential energy associated with phase change and chemical reaction. At equilibrium, the chemical potential of a system is zero. The definition of chemical potential is incredibly important in the study of thermodynamics, particularly when analyzing the Gibbs Free Energy of a system. | ||
Today, we are seeing a lot of interesting industrial applications of | Today, we are seeing a lot of interesting industrial applications of Electric field and electric potential. One that is incredibly interesting is the use of induced electric fields in the separation process of chromatography, which is used to draw compounds out of a mixture by capitalizing on their polarity, solubility, and with the use of electric fields, charge and magnetic affinity. | ||
==History== | ==History== | ||
Revision as of 05:54, 29 November 2016
Claimed by Terrence Connors
Edited by Frederick Erebor
The Main Idea
In physics, many phenomena that we observe are interrelated in some capacity. In the study of electricity and magnetism, several important physical quantities that play a crucial role in understanding physical interactions are derived from one another. Electric Field is a concept that is discussed early in most Electricity and Magnetism curricula, but it has an enormous impact once we discover that it tells us information about Electric Potential, and from that, Potential Energy. This helps physicists to understand both the mechanics of a system and the quantized nature of a system.
A Mathematical Model
We know that the electric force, given by Coulomb's Law, is [math]\displaystyle{ {\vec{F}=q\vec{E}} }[/math]. We also know that electric field and electric force are closely related, the electric field being equal to the electric force divided by the amount of charge [math]\displaystyle{ {\vec{E}=\frac{\vec{F}}{q}} }[/math].
If we think back to the study of conservation of energy, we know that the change in potential energy of a system is work, which is a force being applied over a distance. Since force and distance are vectors, integrating up over the distance of applied force, we obtain: [math]\displaystyle{ {\Delta U=-\int_i^f {\vec{F} • \vec{ds}}} }[/math]. By analogy, we define the electric potential as the energy per coulomb or potential energy divided by charge: [math]\displaystyle{ {\Delta V=-\int_i^f {\vec{E} • \vec{ds}}} }[/math].
Observe both sets of equations: the two for Electric Field and Electric Force, and the two for Electric Potential and Potential Energy. We see that they are all related mathematically. If we integrate the electric force, that is, sum the contributions of force over a finite distance, we obtain the change in potential energy. Dividing by the charge, we obtain the potential difference or electric potential, which we see is simply the integral of the electric field applied over a distance.
A Computational Model
We can model how a system will change in electric potential and potential energy as we move, for example, through a uniform electric field in programs like VPython. One could visualize the electric field, electric force, and quantitatively determine the potential and potential energy as, for instance, a system as simple as a single particle moves through space.
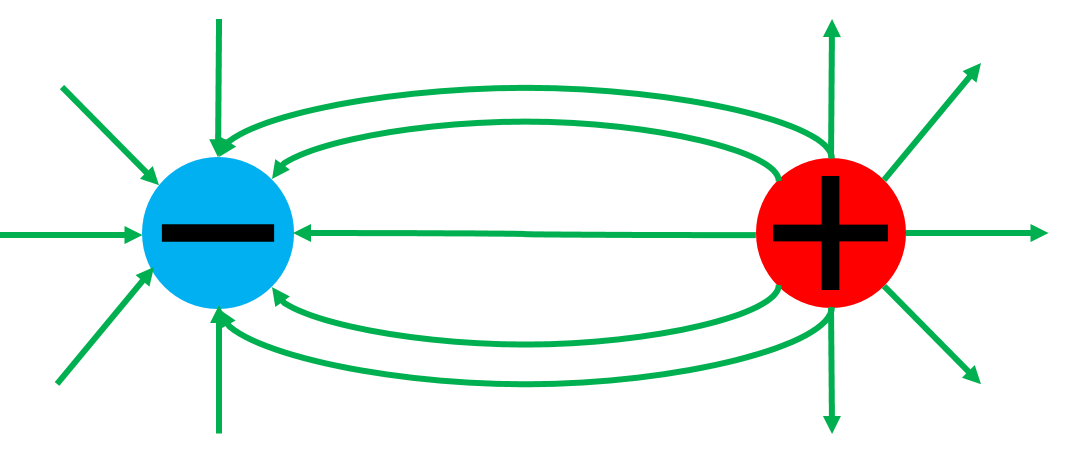
Examples
EXAMPLE 1
The electric field is uniform in this region and
equal to < 0, –300, 0> N/C. B is at < 2, 2, 0> m and
C is at < 2, 0, 0> m. What is ΔV along a path from B to
C?

Solution
In this problem, we are given the electric field and asked to find the change in potential between those two points. The formula that we must apply here is [math]\displaystyle{ \Delta V = -\int_i^f \vec{E} • d\vec{s} }[/math], where the initial point is B and the final point is C, making the distance <2,0,0> m - <2,2,0> m = <0,-2,0> m.
The change in potential therefore is the dot product of the electric field and the change in distance:
-<0,-300,0> N/C • <0,-2,0> m = -600 V
EXAMPLE 2
An HF molecule in the gas phase has an internuclear separation s. We can consider the molecule to be composed of two oppositely charged point charges, H with a positive charge, and F with a negative charge. Calculate the potential difference between points 1 and 2, assuming the distances are much larger than the internuclear separation.

Solution
Here we are asked to find the potential difference between two points on the axis of an electric dipole, as we can determine from the diagram. Since we are told that d>>s, we can approximate the magnitude of the electric field as [math]\displaystyle{ \vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{2p}{r^3} }[/math].
Therefore, we have:
[math]\displaystyle{ V_2 - V_1 = -\int_1^2 \frac{1}{4\pi\epsilon_{0}}\frac{2p}{x^3} dx = -\frac{1}{4\pi\epsilon_{0}}2p \int_1^2\frac{1}{x^3} dx }[/math]
where 1 and 2 are the distances d_1 and d_2 respectively. Integrating, we obtain:
[math]\displaystyle{ \frac {p}{4\pi\epsilon_{0}}(\frac{1}{d_{2}^2}-\frac{1}{d_{1}^2}) }[/math].
We know that p is equivalent to [math]\displaystyle{ \rho s }[/math], so our final answer is [math]\displaystyle{ V_2 - V_1 = \frac{\rho s}{4\pi\epsilon_{0}}(\frac{1}{d_{2}^2}-\frac{1}{d_{1}^2}) }[/math].
Connectedness
The topic of Electric field and electric potential is particularly interesting because it gives scientists and physicists in particular so much insight into the systems they are studying. If we can model the electric field and thus the electric force that an object feels, we gain such a more in-depth understanding of the underlying mechanics of the system, thus enabling us to better model the motion of the system, and understand the energy that the system gains or loses. I think this is incredibly interesting.
There are not many direct impacts of the discussion of electric field and electric potential in the study of Chemical Engineering, but in the study of Chemical Engineering Thermodynamics, this does directly affect chemical potential. Chemical potential is a form of potential energy associated with phase change and chemical reaction. At equilibrium, the chemical potential of a system is zero. The definition of chemical potential is incredibly important in the study of thermodynamics, particularly when analyzing the Gibbs Free Energy of a system.
Today, we are seeing a lot of interesting industrial applications of Electric field and electric potential. One that is incredibly interesting is the use of induced electric fields in the separation process of chromatography, which is used to draw compounds out of a mixture by capitalizing on their polarity, solubility, and with the use of electric fields, charge and magnetic affinity.
History
In the early to mid 18th century, scores of scientists performed countless experiments where they passed electric currents through metal objects and tried to observe the effects that it had. It wasn't until 1831 that the relationship between Electric Field, Potential and Magnetism was determined by Michael Faraday, which is summed up in his principle of electromagnetic induction.
See also
External links
Chemical Potential and Gibbs Distribution
Electric Field and Electric Potential
References
Georgia Institute of Technology. PHYS 2212. Intro Physics II. Lecture Notes. Darnton, Nicholas; Greco, Edwin.