Inclined Plane

Claimed by Catherine Grey Spring 2017

The Main Idea

We typically know an inclined plane as a flat surface that is higher on one end aka a big triangle. Inclined planes are commonly used to move objects to a higher or lower place. These slopes help to lessen the force needed to move an object but do require the object to move a greater distance, the hypotenuse of the triangular plane. Some examples of inclined planes include ramps, stairs, wedges (such as a door stopper), or even mountains which people sled down.

A Mathematical Model

This figure illustrates most of the forces that could act on an inclined plane. Depending on the question not all will be present, specifically friction.

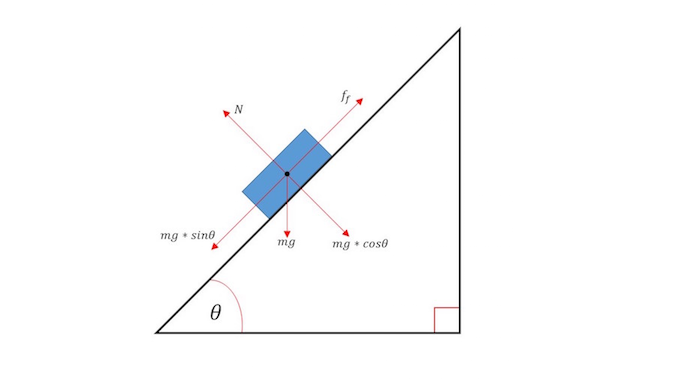
Variables:

θ = Angle of the plane to the horizontal
g = Acceleration due to gravity
m = Mass of object
N = Normal force (perpendicular to the plane)
F_f = frictional force of the inclined plane (sometimes it is omitted on test problems)
mgSinθ = A force parallel to the plane (mgSinθ > Ff the body slides down the plane)
mgCosθ = A force acting into the plane (opposite to N)
F_netparallel = The net parallel force acting on the object
F_{netperpendicular} = The net perpendicular force acting on the object

Equations:

[math]\displaystyle{ \ F_{net} = F_{net//} + F_{netperp} }[/math]

[math]\displaystyle{ \ F_{net//} = F_f - mgSinθ }[/math]

[math]\displaystyle{ \ F_{netperp} = N -mgCosθ }[/math]

Technical Usage

Terminology

Let's imagine there is a right triangle. The side opposite to the right angle is a Slant. The side on the bottom is Run The side vertical to the bottom is Rise

Slope: A slope brings a mechanical advantage to the incline plane.

[math]\displaystyle{ \theta = \tan^{-1} \bigg( \frac {\text{Rise}}{\text{Run}} \bigg) \, }[/math]

Mechanical Advantage

Fw is a gravitational force that applies on the plane
Fi is a force exerted on the object and parallel to the plane

[math]\displaystyle{ \mathrm{MA} = \frac{F_w}{F_i}. \, }[/math]

if the inclined plane is frictionless,

[math]\displaystyle{ \text{MA} = \frac{F_w}{F_i} = \frac {1}{\sin \theta} \, }[/math] (in this case, [math]\displaystyle{ \sin \theta = \frac {\text{Rise}}{\text{Length}} \, }[/math])

if the inclined plane has a friction

[math]\displaystyle{ \mathrm{MA} = \frac {F_w}{F_i} = \frac {\cos \phi} { \sin (\theta - \phi ) } \, }[/math] (in this case, [math]\displaystyle{ \phi = \tan^{-1} \mu \, }[/math])

[math]\displaystyle{ \theta \lt \phi\, }[/math]: Downhill applied force is needed.

[math]\displaystyle{ \theta = \phi\, }[/math]: Infinite mechanical advantage.

[math]\displaystyle{ \theta \gt \phi\, }[/math]: The mechanical advantage is positive. Uphill force is needed.

See Also

Free Body Diagram
Normal Force

References

Cole, Matthew (2008). Explore science, 2nd Ed. Pearson Education. https://books.google.com/books?id=RhuciGEQ1G8C&pg=PA178#v=onepage&q&f=false

http://hyperphysics.phy-astr.gsu.edu/hbase/Mechanics/incline.html