Potential Energy of Macroscopic Springs

An Exploration of Spring Potential Energy: Lanier Freeman and other

Claimed by Hailey Lindstrom for Spring 2017

The Key Concept

A macroscopic ideal spring is an elastic device which stores potential energy when stretched or compressed. Ideal springs exert a force which is linearly proportional to its change in length. This relationship can be modeled by the equation F = -kx, where F is the force, K is the spring constant in N/m or lb/in, and x is the change in length of the spring from its equilibrium length.

Terms and Definitions

A Mathematical Model

The equation for potential energy of a spring can be mathematically shown by integrating Hooke's Law.

• We start with the initial equation for Force of a macroscopic spring, which is equal to:

[math]\displaystyle{ F = kx }[/math]

• We then integrate with respect to x so that we can obtain work (which is equal to the integral of force):

[math]\displaystyle{ \int F\ dx = \int kx\ dx }[/math]

• Finally, we solve the indefinite integral which gives us the final equation for work of a macroscopic spring.

[math]\displaystyle{ W = \Delta U_{spring} = \frac{1}{2}kx^2 }[/math]

Here, work is equal to the elastic spring potential energy, [math]\displaystyle{ \Delta U_{spring} }[/math]

A Computational Model

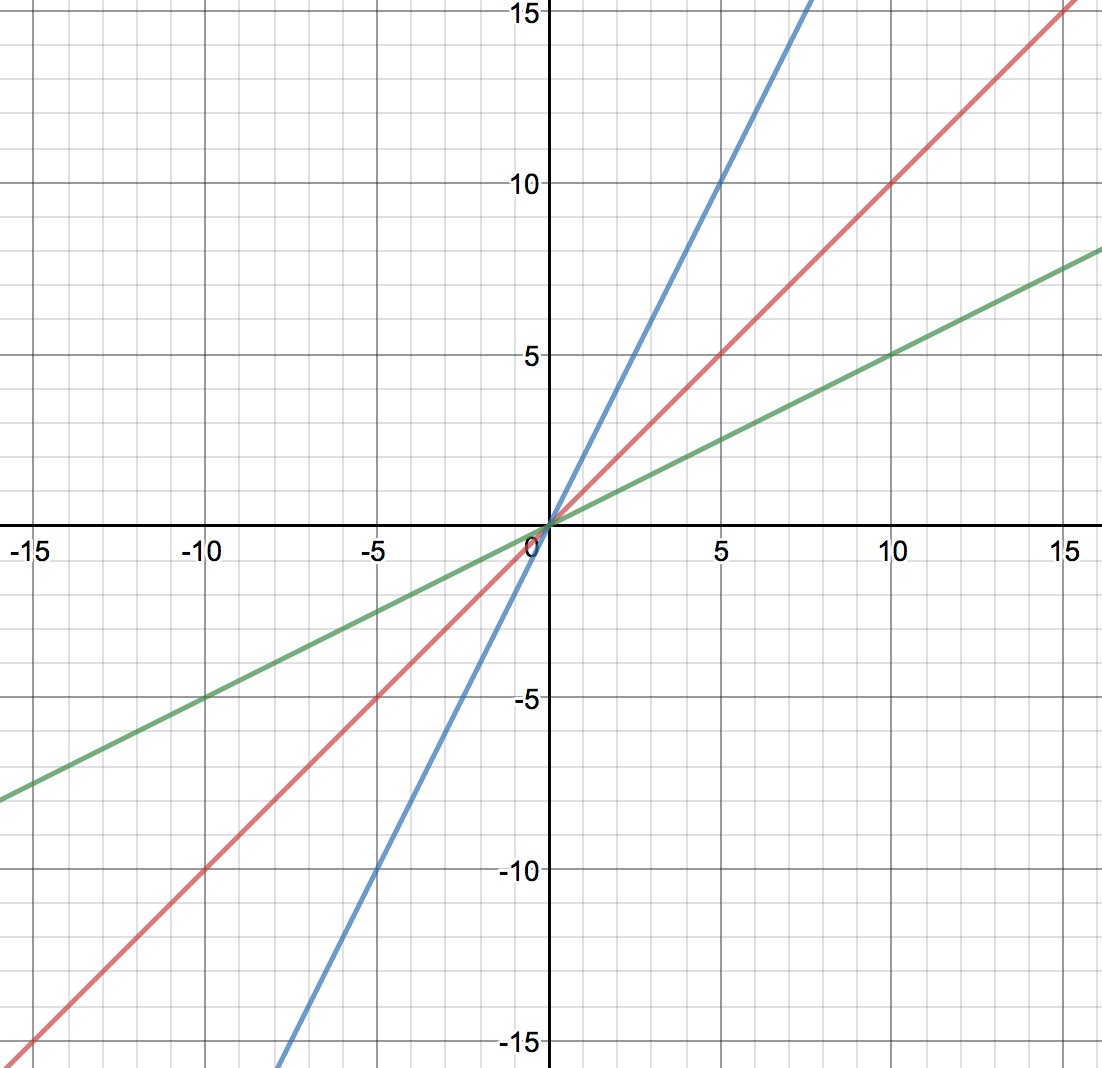
Below is a graph of force versus displacement for a macroscopic spring with different spring constants (k values). The x axis is displacement in meters and the y axis is in Newtons. This shows that there is a linear relationship between change in length and force.

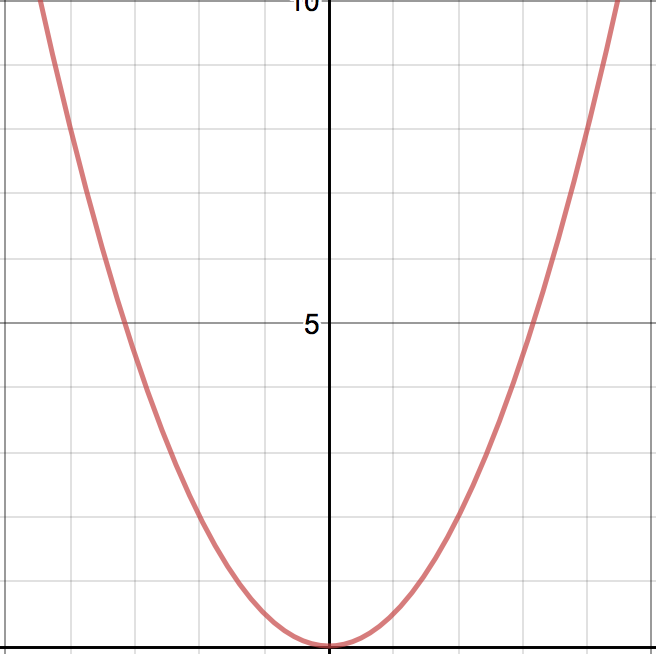
Represented here is the potential energy of the macroscopic spring as a function of the change in length of the spring. The x axis is displacement in meters and the y axis is energy in Joules. This shows that the relationship between change in length and potential energy is quadratic.

Examples

Simple

If a spring has a spring constant, k = 1000 N/m, and is stretched 10 cm, find the force and potential energy of the spring.

Moderate

If a spring has a spring constant, k = 1000 N/m and is stretched 10 cm by an unknown mass, find the unknown mass. File:Moderateexample.jpg

Difficult

If there is a cart of mass, m = 1 kg, moving at speed, v = 10 m/s^2, and it collides with a spring of spring constant, k = 1000 N/m, how far does the spring compress? You can ignore friction in this example!

Connectedness

1. How is this topic connected to something that you are interested in?

This is the first law of thermodynamics where every energy related goes around with this law, where energy is neither made or destroyed. It is very interesting how energy is just there and is transformed into other energies such as chemical energy that the food in the student center has will transform into kinetic energy when playing tennis after school.

1. How is it connected to your major?

As my major is Chemical Engineering, thermodynamics has many materials in common because of calculating the energy balances toward a reaction. The first law of thermodynamics To work out thermodynamic problems you will need to isolate a certain portion of the universe, the system, from the remainder of the universe, the surroundings.

1. Is there an interesting industrial application?

There was an interesting industrial application where we can calculate the energy required by the machine to pump the fluid out.

Lanier's Answers

1. This topic is of much interest to me because of the applications of the mean value theorem of calculus to problems dealing with potential energy--both spring and gravitational. I think this type of problem underscores the amazing power of the MVT.

2. This topic relates to being a math major for obvious reasons; it presents a basic, practical application for advanced mathematics, something that isn't seen often in my experience.

3. A silly yet decent example of industrial applications of spring applications is the way many pens are constructed: A spring of specific dimensions requiring a spring constant within a certain range is necessary to make the button on a pen work.

History

Someone else:

• William Rankinet
  • The term potential energy was introduced e, although it has links to Greek philosopher Aristotle's concept of potentiality.
  • Scottish engineer and physicist
  • links to Greek philosopher Aristotle's concept of potentiality

Lanier:

• Robert Hooke
  • Came up with Hooke's Law, which is used to find the potential energy of springs.
  • Coined the term "cell" in biology

Hailey: Before the existence of coiled springs, leaf springs were used. These springs consisted of curved strips of metal clamped to one another. However, these were not very efficient because they always had to be lubricated and squeaked a lot. It was not until 1763 when R. Tradwell invented the first coiled spring. Finally in 1857 when a steel coil spring was invented. Springs progressed and within just a century, springs have been used in many different things and have substantially improved the car and machine industry.

See also

Someone else: Potential Energy Ideal Spring Spring stretch.

Further reading

Broken link from someone else that I fixed Potential Energy

References

Someone else: [1] [2]

Lanier: [3]