Projectile Motion

claimed by Noah Llorens(Spring 2017)

This page will attempt to analyze projectile motion, a branch of classical mechanics in which the motion of an object (the projectile) is analyzed under the influence of the constant acceleration of gravity, after it has been propelled with some initial velocity.

The Main Idea

Let us imagine firing a cannon, or throwing the ball off of a tower, driving a golf ball off of a tee or even shooting a basketball. All of these are examples of projectile motion. By definition, a projectile has a single force that acts upon it - the force of gravity. If there were any other force acting upon an object, then that object would not be a projectile. Thus projectile motion is motion under the primary action of gravity where the initial velocity in some horizontal direction is not zero.

A Mathematical Model

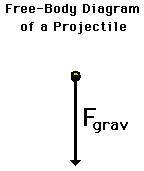
Regardless of whether a projectile is moving upwards, downwards, upwards and rightwards, or downwards and leftwards, the free-body diagram of the projectile is still modeled as an object upon which the only force is gravity. Thus, the free-body diagram of a projectile would show a single force acting downwards and labeled force of gravity (or simply Fgrav).

[math]\displaystyle{ \vec{F}_{grav} = -mg\hat{y} }[/math]

              where m is the mass of the projectile and 
                    g represents the acceleration due to Earth's gravitational field.

A Computational Model

One method used to visualize or predict a projectiles trajectory is to apply our mathematical model using computational programming. Please see the following Projectile Motion Video for a detailed computational model including animation of a projectile in motion. For this computational model I used V-Python!

Examples

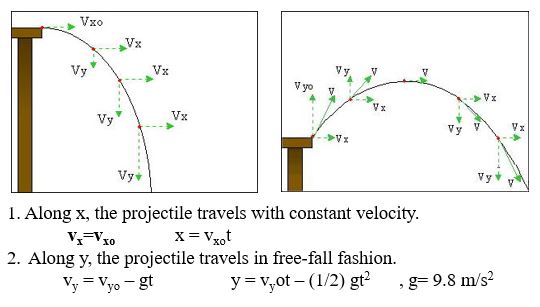
A projectiles trajectory most closely resembles a parabola. Lets return to one of our previously listed examples of projectile motion, a canon.

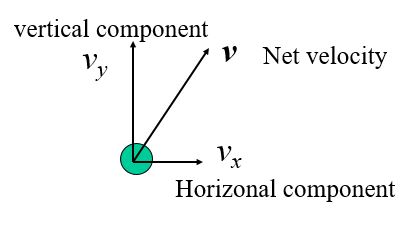
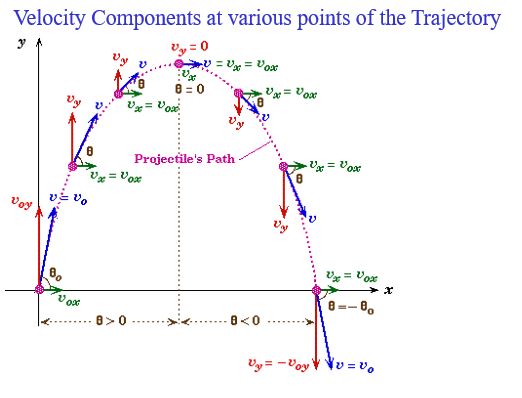
We see here that the velocity can be broken into components which can then be analyzed as the projectile moves along its intended path.

It is important to note that for this analysis we made many simplifying assumptions including, that the acceleration due to gravity remains constant because our object is very close to earth, its size is small enough to be modeled as a point mass where irregularities in shape can be neglected, also there are no resistive forces acting on our object that would affect its motion such as drag!

Connectedness

Projectile motion represents my most cherished triumph in developing my skills in physics analysis. I chose the topic of Projectile Motion because it was my primary introduction to Kinetics and Kinematics. For me, the study of projectile motion was a relevant and practical analysis that allowed me to analyze something that I could visualize and tangibly model. If ever there was a problem that I didn't understand, it was easy to represent the projectile in my own model and derive a reasonable approximation or solution. Analysis of projectile motion made me confident in my own physics intuition! After all my first physics teacher used to always say, "If gravity is about 10, does your answer make sense?"

History

Major contributions to our current understanding of Projectile Motion

Aristotle

The first findings of Projectile Motion were contributed by Aristotle. He believed that a projectile modeled by a canon ball travels in a straight line until it lost its 'impetus'. When it lost its 'impetus' which ran out after time, due to a restive force, the projectile would immediately drop and fall to the ground. For objects projected over short distances, at first observation this can visually appear to be true.

Galileo

Galileo's findings were motivated by the Renaissance. At the time people were searching for a way to model 3-D objects in our 2-D world. Through as series of experiments he discovered that projectile motion is a result of Free Fall Motion along the y-axis and Uniform Motion along x-axis. This model is more well known and represents a more clearer understanding, one that is more widely accepted modern day.

See also

For more objects in motion see Curving Motion

External links

Interactive Projectile Simulator Projectile Simulator Horizontally-Launched Projectiles Angle-Launched Projectiles

References

The following references were used while writing this page:

https://www.phy.duke.edu/~rgb/Class/intro_physics_1/intro_physics_1.pdf http://www.physicsclassroom.com/class/vectors/Lesson-2/What-is-a-Projectile