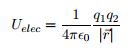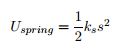The Energy Principle

claimed by Sunil Mutyala

The basis of the energy principle can be described with the statement, "energy can neither be created nor destroyed."

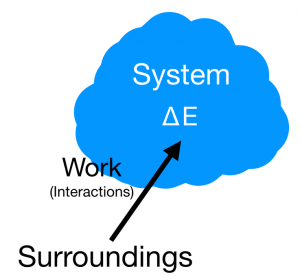
The energy principle is used to describe changes in energy on a system. These energies can take numerous different forms including Kinetic Energy, Potential Energy, Chemical Energy, Rest Energy, and Thermal Energy. The change in energy of the system should be equal to the energy inputs from surroundings.

The Main Idea

The Energy Principle, also referred to as The First Law of Thermodynamics, defines the transfer of energy between systems. It is defined with the fact that the change of the energy of system is equal to the work surrounding in addition to heat transfers from the surroundings as well. This principle is defined with the equation

ΔEsys=Wsurr+Q or, a more simplified version, ΔEsys=(Energy inputs from surroundings)

This number can be positive or negative.

There are many ways to use the energy principle; most of the problems you will encounter will have no work acting on the system and no transfer of heat, thus E_sys,initial = E_sys,final. Otherwise you will use E_sys,initial + Wsurr+Q = E_sys,final. The first step in using the Energy Principle is to identify which initial and final energies have values in the equation. You can eliminate the values that are not present in the equation for the specific problem in order to simplify the solution of the problem. Additionally there may be multiple potential energies in the scenario that need to be included when solving the equation including Spring Potential Energy, Gravitational Potential Energy, Electric Potential Energy, and Gravitational Potential Energy near the surface of the Earth. Generally, if an initial or final state has zero velocity, the kinetic energy will be zero for that state. It's also key to note that potential energy is zero at very large distances. The basic equation involving only kinetic and potential energy will often look like the following equation: Esys=(K1+K2+K3+…)+(U1,2+U1,3+U2,3+…) The eqations involving more energies can be seen in the Mathematical Models section.

Mathematical Models

NOTE: These are a lot of equations, but don't get overwhelmed. You simply have to pick and choose which ones are necessary for the problem given; examples are shown below. For in-depth explanations on each type of energy, look at the associated pages on the Main Page or click on the links in the 'See also' section below.

The Energy Principle
EQ 1: [math]\displaystyle{ {∆E} = {Q + W} }[/math] where [math]\displaystyle{ {Q} }[/math] is heat and [math]\displaystyle{ {W} }[/math] is the amount of work acting on the system.

EQ 2: [math]\displaystyle{ {∆E} = {∆K + ∆E_{Rest} + ∆U + ∆E_{Thermal}} }[/math] - the different types of energy that can be associated with a given particle in a system. Not all have to be present.

EQ 3: [math]\displaystyle{ E_{Rest}=mc^2 }[/math] - Rest Energy, where m is the mass and c is the speed of light.

EQ 4: [math]\displaystyle{ K=\frac{1}{2}mv² }[/math] - Kinetic Energy, where m is the mass and v is the velocity (for speeds less than the speed of light).

EQ 5: [math]\displaystyle{ ∆E_{Thermal} = mC∆T }[/math] - Thermal energy, were m is the mass, C is the specific heat of water (4.2 J/g/K), and T is temperature.

Potential Energy Equations:

EQ 6: 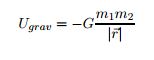. - for use when not near the Earth's surface

EQ 7: .

EQ 8: .

EQ 9: .

A Computational Model

This is a good visualization of kinetic, potential, and total energy.

Energy Skate Park

Examples

Simple

An 8.4 kg box is pushed off of a cliff 72.2 m high. What is the velocity of the box right before it hits the ground?

Solution:

In this scenario, the work done from the surroundings is equal to zero and the transfer of heat is zero as well. Therefore, ΔEsys= 0. As shown in the solution below the initial kinetic energy is equal to zero because there is no initial velocity and the final potential energy is equal to zero because the final height is zero. The only potential energy needed for the solution of this problem is gravitational potential energy near the surface of the Earth.

Difficult

A 90 kg machine is moving with a speed of 4.7 m/s. A man tries to slow it down by pushing it in the opposite direction of its movement for 2.7 m at an average force of 215 N. What is the speed of the box after the man stops pushing the machine?

Solution:

There is no transfer of heat so Q is eliminated from The Energy Principle equation. The equation you would use is ΔEsys= W. Additionally, the work is negative in this scenario because the force is in the opposite direction of momentum. There is no potential energy of any sort.

Connectedness

The Energy Principle can be used for a variety of situations; the fact that it can tell us something about the work acting on a system with only knowing about what energies are present (and vice versa) is what makes this such a fundamental principle. The energy principle is also used to describe the conservation of energy, which is something I find pretty interesting. Energy doesn't just disappear, it's simply converted into a different form. This topic has a huge connection to my major, Biology, because chemical energy (obtained from food) is necessary for a healthy and active body.

History

The concept of energy and its connection to the amount of work performed goes way back to the age of steam engines; physicists and engineers came up with this notion to describe how mechanically and thermally efficient their machines were. In the 1850's, people like William Thomson and William Rankine began to come up with terms like 'kinetic energy' and 'potential energy.' After the 1920's, this study of science became to be known as thermodynamics, the science of energy transformations. This led to the laws of thermodynamics, one of which relates to the conservation of energy.

See also

Potential Energy
Rest Mass Energy
Kinetic Energy
Work
Thermal Energy
Gravitational Potential Energy
Conservation of Energy
Spring Potential Energy

Further reading

Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 6

External links

http://hyperphysics.phy-astr.gsu.edu/hbase/conser.html#coneng
http://hyperphysics.phy-astr.gsu.edu/hbase/enecon.html

References

http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:define_energy
http://www.texample.net/tikz/examples/earth-orbit/
https://en.wikipedia.org/wiki/Conservation_of_energy
https://en.wikipedia.org/wiki/History_of_energy Chabay, Ruth W., and Bruce A. Sherwood. Matter and interactions. Hoboken: Wiley, 2015. Print.