Electric Field

CLAIMED BY JAY SHAH PHYS 2212 3/13/2016 EDITED BY YASMIN MARTINS 10/31/2016

EDIT CLAIMED BY QUINTIN MURPHY 4/8/2017 EDIT BY KEVIN RUDDY 4/9/2017 hey Kevin I am still editing this, please do not update. -Quintin.

This page discusses the general properties of electric fields.

The Main Idea

The main idea of this page is to get an understanding of how electric fields behave.

History

Electric fields are created by electric charges. The original discovery of the electric charge is not explicitly known, but in 1675 the esteemed chemist Robert Boyle, known for Boyle's Law, discovered the attraction and repulsion of certain particles in a vacuum. Almost 100 years later in the 18th century the American Benjamin Franklin first coined the phrases positive and negative (later developed into proton and electron) for these particles with attractive and repulsive properties. Finally, in the 19th century Michael Faraday utilized his electrolysis process to discover the discrete nature of electric charge.

Electric Field

Electric Field is a field created by an electric charge. It is measured in units of newtons per coulomb (N/C), the proper units of which are (kg*(m/s^2)), and has a direction, making it a vector quantity. Electric fields can also be in the units of volts per meter (V/m). The electric field created by a charge exists at all points in space and exerts a force on other charged objects. The field can be drawn as an arrow with tail at the observation location pointing in the direction of the field. The Electric field obeys superposition, so the net Electric field at a point in space can be determined by summing all the individual fields present at that location.

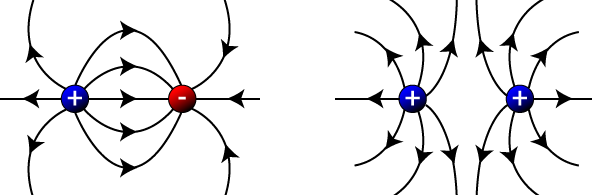
The electric field of a positive particle points away from the particle, while the electric field of a negative particle points toward the particle, as seen right here:

When two oppositely charged particles are placed next to each other, their electric field moves from the positive to the negative. Two similarly charged particles will have fields that are repelled by each other. This is shown below:

The two oppositely charged particles, when in very close proximity, will act together in the form of a dipole.

Mathematical Concept of a Field

In mathematics, a field is a value that exists at all points in space. The magnitude of an electric field is a scalar. The field itself is represented as a vector: <x,y,z>. Other examples of fields are gravitational fields and magnetic fields.

You can calculate electric field in a few ways. You can calculate the electric field vector and magnitude by using the following equations:

[math]\displaystyle{ E = \frac{F}{q} }[/math], where F is the force and q is the charge of the particle. This formula is very helpful to think about to understand the relation between force and electric field.

[math]\displaystyle{ E = \frac{kQ}{r^2} }[/math], where k is Coulomb's constant, or 9x10^9, Q is the charge of the particle, and r is the distance between both particles.

The magnitude of an electric field can be also be calculated by using the potential difference, Δϕ, between two plates and the distance, d, between them.

[math]\displaystyle{ E = -\frac{\Delta\phi}{d} }[/math]

Electric Field and Force

The force due to an external electric field on a charged particle is given by the equation [math]\displaystyle{ \vec{F} = q\vec{E} }[/math] where q is the charge of the observed particle and E is the electric field. The field created by a charged particle exerts no force on itself. This is to say that the force on a given particle is defined as the charge on that particle multiplied the combined electric fields of the external environment. Since force is measured in Newtons (N) and charge in Coulombs (C), Electric field is measured in Newtons per Coulomb (N/C) as mentioned earlier. Furthermore, the magnitude of an electric field is not dependent on the sign of q (i.e. whether the charge is positive or negative.) The sign only helps determine the direction that the electric field points.

To calculate the electric force on a particle, first you must calculate the electric fields affecting the particle. Applying superposition, you add all electric fields to find the net field. Once you have this, you multiply the electric field by the charge of the particle, and this gives you the force exerted on the particle. Like charges repel each other and opposite charges attract each other.

Electric Field and Superposition

The electric field contributed by a charged particle is unaffected by the electric field contributed by other charged particles. To that end, the principle of superposition, as mentioned earlier, states that the net electric field at a location is determined by the sum of all individual electric fields on charged particles. The principle of superposition is very useful to determine the force on a given charged particle. By being able to define electric field as a vector and simply adding up the various components of individual electric fields, the force on a particle is easily calculated using [math]\displaystyle{ \vec{F} = q\vec{E} }[/math]

The two must common methods of combining vectors in the principle of superposition are the tail to tail method (number 1 in the image below) and head to tail (number 2 in the image below).

File:Vector superposition.jpg

Electric Field and Electric Potential

Another way to define electric field is using the electric potential over a certain distance to determine field. In this case, Electric field is shown in units volts (V) per meter (m) (V/m). Again, electric field is calculated with potential difference with the equation: [math]\displaystyle{ E = -\frac{\Delta\phi}{d} }[/math]

Examples

Simple

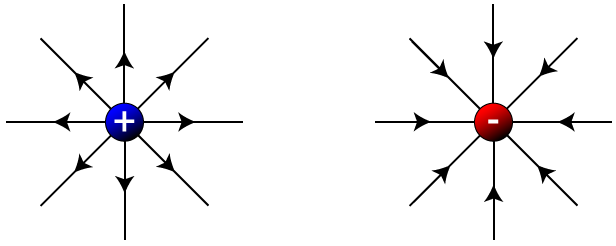
Select all of the arrows that accurately show the electric field produced by the charge shown. (only direction not magnitude) We know that the electric field from a single point charge will always point outwards if it is positive and always inwards if it is negative. This means that A and C are both correct. It is also important to remember that opposites will attract. In this case a negative and positive charge will attract to one another in any orientation. It is also important to remember that oppositely charged particles will repel each other, so any negative-negative or positive-positive interaction will result in a repelling force.

Middling

What is the magnitude and direction of the electric field at the origin (assume Q = 1 coulomb)?

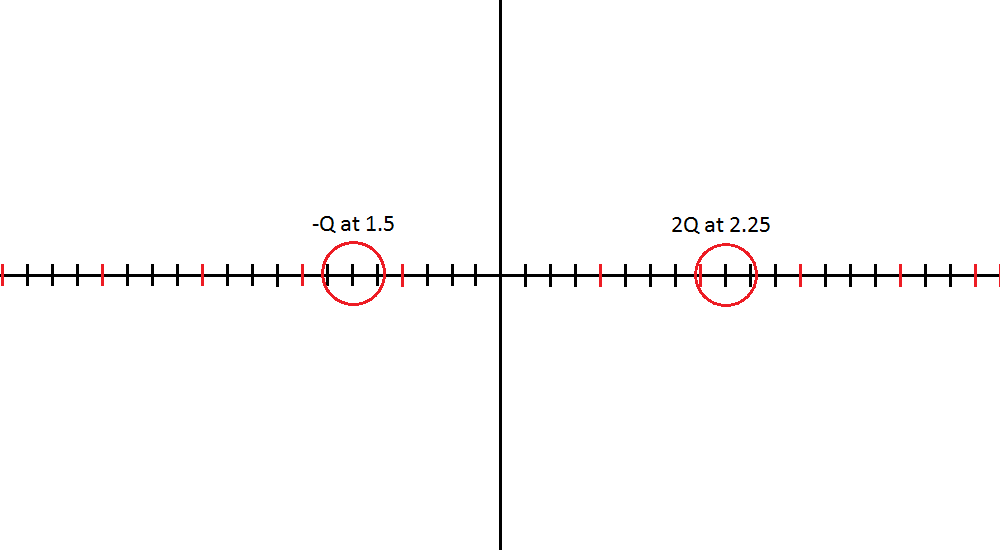
There is a positive charge on the right with an electric field pointing to the left at the origin. The negative charge on the left also has an electric field pointing to the left at the origin so we will add the two electric fields as they point along the negative x axis. [math]\displaystyle{ \frac{k}{1.5^2}+\frac{k*2}{2.25^2} = 0.75*10^{10} }[/math]

See also

The understanding of electric fields is a doorway into all the various fields only some of which will be covered in physics 2212. The fundamental understanding of electric fields will prove to be very important further along when magnetic fields are introduced as they share many qualities. Some quality material can be found at:

Electric Force (as we discussed [math]\displaystyle{ \vec{F} = q\vec{E} }[/math] )

External links

A youtube playlist that does a great job going step by step and reviewing topics

Further review on electric field lines.

Get a better understanding of fields through hands on manipulation. This can be very helpful for getting an intuitive understanding of fields.

References

This section contains the the references you used while writing this page