Python Syntax: Difference between revisions
No edit summary |
Added a basic Python tutorial, cleaned up the page some. Will be back to clean up some more and improve upon the VPython tutorial itself. |
||
| Line 1: | Line 1: | ||
Edited by | Edited by Zach Sanchez - Fall 2017 (in progress) | ||
==The Main Idea== | ==The Main Idea== | ||
VPython is an extension of the Python programming language that contains a 3D graphics module called Visual, which allows users to create simple simulations of physics problems. Its primary use is for educational purposes, although it has been used in research before in the past. We will use VPython on occasion to aid us in visualizing and experimenting with the ideas that we learn in this course. | |||
VPython | |||
==Downloading vPython== | |||
In all cases you will need to have Python 2.7.9 installed. Future versions may also work, but be warned that it may cause VPython to behave erratically. | |||
[http://vpython.org/contents/download_windows.html For Windows] | |||
[http://vpython.org/contents/download_mac.html For Mac] | |||
[http://vpython.org/contents/download_linux.html For Linux] | |||
Note for Linux: You can only install Classic VPython, which is no longer supported and may be missing some features and bug fixes that are present in the current version of VPython. | |||
Alternatively, you can use GlowScript, a virtual environment that allows you to execute VPython code in your browser. You can create an account at [http://www.glowscript.org/ http://www.glowscript.org/]. | |||
==Python Basics== | |||
It's always helpful to have a background knowledge of Python, however basic, before proceeding with the applications more relevant to this course. | |||
# Comments start with a number symbol. Use these liberally in order to keep track of the changes you make/the code you write. | |||
# We're always going to start our programs with the following headers to ensure that math works correctly. | |||
from__future__ import division | |||
from visual import* | |||
# Math works as you would expect. | |||
1 + 1 # -> 2 | |||
2 - 1 # -> 1 | |||
3 * 2 # -> 6 | |||
8 / 4 # -> 4 | |||
(1 + 3) * 2 # -> 8 | |||
1 + (3 * 2) # -> 7 | |||
# That is, until you need to do an exponent. But you shouldn't encounter anything much weirder than that math-wise. | |||
2 ** 3 # -> 8 | |||
= | # However, these math operations are useless if we don't store the values anywhere. | ||
x = 1 + 1 | |||
# Now if you try to access x in the future, it will have the value of '2'. | |||
# You can print your variables like this: | |||
print(x) | |||
# You can also add in some text with them like this: | |||
print("The value of x is ", x) | |||
# Sometimes we only want to execute something based on a certain condition. | |||
if x == 2: | |||
y = 3 | |||
# The '==' means that you're directly comparing two values. If they're equal, whatever is on the inside of the if-statement will be executed. | |||
# Now is a good time to note that whitespace is very important in Python. 'y = 3' will always execute if it isn't tabbed, so even if x is equal to 7, y will still become 3. | |||
# If you ever see me use whitespace in this tutorial, make sure you do as well. | |||
# Some other useful comparators: != (not equal), >, >= (greater than or equal to), <, <= (less than or equal to), 'and', 'or', 'not' | |||
# You can add onto the above if-statement by tacking on: | |||
elif x == 3: | |||
y = 4 | |||
else: | |||
y = 5 | |||
# With elif meaning "else if" for a second possible condition, and "else" for something that you want to execute if none of the earlier conditions are met. | |||
# You can also have a loop that executes code for a certain amount of time or based on a certain condition. | |||
while x < 5: | |||
print("x is ", x) | |||
x = x + 1 | |||
# This will output the value of x up until it reaches 4. | |||
Thus concludes our very, very brief foray into Python. That was simply the bare minimum required to understand what will be needed for this class. More concepts will be introduced as needed, whether that be in this tutorial or in a lab. For a more complete understanding of Python, you can look up other Python tutorials elsewhere on the Internet. | |||
==Mathematical Model== | |||
Vpython can compute any equation, but some that may be most helpful and most useful for Physics can be found below. (Keep in mind you can alter these numbers to be whatever you need, these are just to provide an example): | |||
To update momentum: | To update momentum: | ||
pf = pi + Fnet*deltat | pf = pi + Fnet*deltat | ||
To update position: | To update position: | ||
objectf.pos = objecti.pos + (pcart/mcart)*deltat | objectf.pos = objecti.pos + (pcart/mcart)*deltat | ||
To create a vector: | To create a vector: | ||
vector(0,0,0) -- fill in with whatever numbers the vector should be | vector(0,0,0) -- fill in with whatever numbers the vector should be | ||
Gravitational Force: | Gravitational Force: | ||
# Constants | |||
G = 6.7e-11 | |||
G = 6.7e-11 | mEarth = 6e24 | ||
mcraft = 15e3 | |||
mEarth = 6e24 | deltat = 60 | ||
t = 0 | |||
mcraft = 15e3 | |||
deltat = 60 | |||
t = 0 | |||
Finds the change in position: | Finds the change in position: | ||
r=craft.pos-Earth.pos | r=craft.pos-Earth.pos | ||
m=mcraft | |||
m=mcraft | |||
To find the magnitude of the change in position: | To find the magnitude of the change in position: | ||
rmag= mag(r) | |||
rmag= mag(r) | |||
To calculate the new magnitude of gravitational force: | To calculate the new magnitude of gravitational force: | ||
Fmag=(G*mcraft*mEarth)/(rmag**2) | |||
Fmag=(G*mcraft*mEarth)/(rmag**2) | |||
To calculate the direction of the change in position: | To calculate the direction of the change in position: | ||
rhat=r/rmag | |||
rhat=r/rmag | |||
To calculate net force: | To calculate net force: | ||
Fnet=-Fmag*rhat | Fnet=-Fmag*rhat | ||
To calculate spring force: | To calculate spring force: | ||
L0 = 0.3 | L0 = 0.3 | ||
Lvec = ball.pos - ceiling.pos | |||
Lvec = ball.pos - ceiling.pos | Lhat = norm(Lvec) | ||
Lmag = mag(Lvec) | |||
Lhat = norm(Lvec) | Fspr = (-ks)*(Lmag - L0)*(Lhat) | ||
Lmag = mag(Lvec) | |||
Fspr = (-ks)*(Lmag - L0)*(Lhat) | |||
To calculate kinetic energy: | To calculate kinetic energy: | ||
Kinetic = (1/2)*(mball*(vel**2)) | Kinetic = (1/2)*(mball*(vel**2)) | ||
To create a graph: | To create a graph: | ||
gdisplay(width=500, height=250, x=600, y=1) | gdisplay(width=500, height=250, x=600, y=1) | ||
ygraph= gcurve(color=color.cyan) | |||
ygraph= gcurve(color=color.cyan) | |||
To add plots to the graph: | To add plots to the graph: | ||
ygraph.plot(pos=(t, fnet.y)) | ygraph.plot(pos=(t, fnet.y)) | ||
==Computational Model== | ==Computational Model== | ||
VPython is used to create computational, 3D models of various real world situations in order to better visualize how different equations can manipulate different scenarios. This is very valuable since many of the equations and situations that are coded in vPython are extremely difficult to make a functioning model of in real life. | VPython is used to create computational, 3D models of various real world situations in order to better visualize how different equations can manipulate different scenarios. This is very valuable since many of the equations and situations that are coded in vPython are extremely difficult to make a functioning model of in real life. | ||
For instance, the picture below is an example of program that was programmed to show the orbit of a craft around Earth. | For instance, the picture below is an example of program that was programmed to show the orbit of a craft around Earth. | ||
[[File:Earthorbits.jpg]] | [[File:Earthorbits.jpg]] | ||
This picture shows a graph that tracks. | This picture shows a graph that tracks. | ||
[[File:PositionGraph.jpg]] | [[File:PositionGraph.jpg]] | ||
==Examples== | ==Examples== | ||
| Line 152: | Line 153: | ||
Sphere: | Sphere: | ||
sphere= sphere(pos=vector(-4,-2,5), radius=.4, color=color.red) | sphere= sphere(pos=vector(-4,-2,5), radius=.4, color=color.red) | ||
Arrow: | Arrow: | ||
bt=arrow(pos=sphere.pos, axis=sphere2.pos-sphere.pos, color=color.cyan) | bt=arrow(pos=sphere.pos, axis=sphere2.pos-sphere.pos, color=color.cyan) | ||
Vector: | Vector: | ||
vector=vector(0, 0, 0) | vector=vector(0, 0, 0) | ||
Trail: | Trail: | ||
trail = curve(color=sphere.color) | trail = curve(color=sphere.color) | ||
trail.append(pos=sphere.pos) | |||
trail.append(pos=sphere.pos) | |||
Setting Scene Range: | Setting Scene Range: | ||
scene.range=11*sphere.radius | scene.range=11*sphere.radius | ||
Helix: | Helix: | ||
spring = helix(pos=ceiling.pos, color=color.cyan, thickness=.003, coils=40, radius=0.015) | spring = helix(pos=ceiling.pos, color=color.cyan, thickness=.003, coils=40, radius=0.015) | ||
Intermediate: | Intermediate: | ||
| Line 183: | Line 182: | ||
Setup graphing windows: | Setup graphing windows: | ||
gdisplay(width=500, height=250, x=600, y=1) | gdisplay(width=500, height=250, x=600, y=1) | ||
ygraph = gcurve(color=color.yellow) | |||
ygraph = gcurve(color=color.yellow) | gdisplay(width=500, height=250, x=600, y=300) | ||
gdisplay(width=500, height=250, x=600, y=300) | |||
Plotting: | Plotting: | ||
pgraph = gcurve(color=color.blue) | pgraph = gcurve(color=color.blue) | ||
ygraph.plot(pos=(time, Fnet.y)) | |||
ygraph.plot(pos=(time, Fnet.y)) | pgraph.plot(pos=(time, sphere.y)) | ||
pgraph.plot(pos=(time, sphere.y)) | |||
Difficult: | Difficult: | ||
| Line 202: | Line 196: | ||
Using Loops to update Equations: | Using Loops to update Equations: | ||
Constants: | |||
G = ? | G = ? | ||
| Line 217: | Line 210: | ||
t = ? | t = ? | ||
Objects and initial values: | |||
Earth = sphere(pos=vector(0,0,0), radius=6.4e6, color=color.cyan) | |||
scene.range=11*Earth.radius | |||
Earth = sphere(pos=vector(0,0,0), radius=6.4e6, color=color.cyan) | Moon = sphere(pos=(4e8, 0, 0), radius=1.75e6, color=color.white) | ||
scene.range=11*Earth.radius | |||
Moon = sphere(pos=(4e8, 0, 0), radius=1.75e6, color=color.white) | |||
Add a radius for the spacecraft. It should be BIG, so it can be seen: | Add a radius for the spacecraft. It should be BIG, so it can be seen: | ||
craft = sphere(pos=vector(-6.656e7,-3.648e6,0), radius= 10000, color=color.yellow) | craft = sphere(pos=vector(-6.656e7,-3.648e6,0), radius= 10000, color=color.yellow) | ||
vcraft = vector(206, 2645,0) | vcraft = vector(206, 2645,0) | ||
pcraft = mcraft*vcraft | pcraft = mcraft*vcraft | ||
pArrow=arrow(color=color.green) | pArrow=arrow(color=color.green) | ||
fArrow=arrow(color=color.cyan) | fArrow=arrow(color=color.cyan) | ||
dpArrow=arrow(color=color.red) | dpArrow=arrow(color=color.red) | ||
Fnet_tangent_arrow = arrow(color=color.yellow) | Fnet_tangent_arrow = arrow(color=color.yellow) | ||
Fnet_perp_arrow= arrow(color=color.magenta) | Fnet_perp_arrow= arrow(color=color.magenta) | ||
This creates a trail for the spacecraft: | This creates a trail for the spacecraft: | ||
trail = curve(color=craft.color) | trail = curve(color=craft.color) | ||
And this prevents zooming in or out: | And this prevents zooming in or out: | ||
scene.autoscale = 0 | scene.autoscale = 0 | ||
pscale=Earth.radius/mag(pcraft) | pscale=Earth.radius/mag(pcraft) | ||
fscale=Earth.radius/((G*mEarth*mcraft)*mag(craft.pos-Earth.pos)**2) | fscale=Earth.radius/((G*mEarth*mcraft)*mag(craft.pos-Earth.pos)**2) | ||
dpscale=500*Earth.radius/mag(pcraft) | dpscale=500*Earth.radius/mag(pcraft) | ||
print("p=", pcraft) | print("p=", pcraft) | ||
Calculations: | |||
Sets time for loop to run: | Sets time for loop to run: | ||
while t < 165240: | while t < 165240: | ||
This slows down the animation (runs faster with bigger number): | This slows down the animation (runs faster with bigger number): | ||
rate(10000) | rate(10000) | ||
Add statements here for the iterative update of gravitational | |||
force, momentum, and position. | |||
r = craft.pos-Earth.pos | r = craft.pos-Earth.pos | ||
rmag = sqrt(r.x**(2)+r.y**(2)+r.z**(2)) | rmag = sqrt(r.x**(2)+r.y**(2)+r.z**(2)) | ||
| Line 295: | Line 286: | ||
scene.range=craft.radius*600 | scene.range=craft.radius*600 | ||
Uncomment these two lines to exit the loop if | Uncomment these two lines to exit the loop if | ||
the spacecraft crashes onto the Earth. | the spacecraft crashes onto the Earth. | ||
| Line 305: | Line 294: | ||
trail.append(pos=craft.pos) | trail.append(pos=craft.pos) | ||
t = t+deltat | t = t+deltat | ||
Revision as of 14:49, 1 November 2017
Edited by Zach Sanchez - Fall 2017 (in progress)
The Main Idea
VPython is an extension of the Python programming language that contains a 3D graphics module called Visual, which allows users to create simple simulations of physics problems. Its primary use is for educational purposes, although it has been used in research before in the past. We will use VPython on occasion to aid us in visualizing and experimenting with the ideas that we learn in this course.
Downloading vPython
In all cases you will need to have Python 2.7.9 installed. Future versions may also work, but be warned that it may cause VPython to behave erratically.
Note for Linux: You can only install Classic VPython, which is no longer supported and may be missing some features and bug fixes that are present in the current version of VPython.
Alternatively, you can use GlowScript, a virtual environment that allows you to execute VPython code in your browser. You can create an account at http://www.glowscript.org/.
Python Basics
It's always helpful to have a background knowledge of Python, however basic, before proceeding with the applications more relevant to this course.
# Comments start with a number symbol. Use these liberally in order to keep track of the changes you make/the code you write. # We're always going to start our programs with the following headers to ensure that math works correctly. from__future__ import division from visual import*
# Math works as you would expect. 1 + 1 # -> 2 2 - 1 # -> 1 3 * 2 # -> 6 8 / 4 # -> 4 (1 + 3) * 2 # -> 8 1 + (3 * 2) # -> 7
# That is, until you need to do an exponent. But you shouldn't encounter anything much weirder than that math-wise. 2 ** 3 # -> 8
# However, these math operations are useless if we don't store the values anywhere. x = 1 + 1 # Now if you try to access x in the future, it will have the value of '2'.
# You can print your variables like this:
print(x)
# You can also add in some text with them like this:
print("The value of x is ", x)
# Sometimes we only want to execute something based on a certain condition.
if x == 2:
y = 3
# The '==' means that you're directly comparing two values. If they're equal, whatever is on the inside of the if-statement will be executed.
# Now is a good time to note that whitespace is very important in Python. 'y = 3' will always execute if it isn't tabbed, so even if x is equal to 7, y will still become 3.
# If you ever see me use whitespace in this tutorial, make sure you do as well.
# Some other useful comparators: != (not equal), >, >= (greater than or equal to), <, <= (less than or equal to), 'and', 'or', 'not'
# You can add onto the above if-statement by tacking on:
elif x == 3:
y = 4
else:
y = 5
# With elif meaning "else if" for a second possible condition, and "else" for something that you want to execute if none of the earlier conditions are met.
# You can also have a loop that executes code for a certain amount of time or based on a certain condition.
while x < 5:
print("x is ", x)
x = x + 1
# This will output the value of x up until it reaches 4.
Thus concludes our very, very brief foray into Python. That was simply the bare minimum required to understand what will be needed for this class. More concepts will be introduced as needed, whether that be in this tutorial or in a lab. For a more complete understanding of Python, you can look up other Python tutorials elsewhere on the Internet.
Mathematical Model
Vpython can compute any equation, but some that may be most helpful and most useful for Physics can be found below. (Keep in mind you can alter these numbers to be whatever you need, these are just to provide an example):
To update momentum:
pf = pi + Fnet*deltat
To update position:
objectf.pos = objecti.pos + (pcart/mcart)*deltat
To create a vector:
vector(0,0,0) -- fill in with whatever numbers the vector should be
Gravitational Force:
# Constants G = 6.7e-11 mEarth = 6e24 mcraft = 15e3 deltat = 60 t = 0
Finds the change in position:
r=craft.pos-Earth.pos m=mcraft
To find the magnitude of the change in position:
rmag= mag(r)
To calculate the new magnitude of gravitational force:
Fmag=(G*mcraft*mEarth)/(rmag**2)
To calculate the direction of the change in position:
rhat=r/rmag
To calculate net force:
Fnet=-Fmag*rhat
To calculate spring force:
L0 = 0.3 Lvec = ball.pos - ceiling.pos Lhat = norm(Lvec) Lmag = mag(Lvec) Fspr = (-ks)*(Lmag - L0)*(Lhat)
To calculate kinetic energy:
Kinetic = (1/2)*(mball*(vel**2))
To create a graph:
gdisplay(width=500, height=250, x=600, y=1) ygraph= gcurve(color=color.cyan)
To add plots to the graph:
ygraph.plot(pos=(t, fnet.y))
Computational Model
VPython is used to create computational, 3D models of various real world situations in order to better visualize how different equations can manipulate different scenarios. This is very valuable since many of the equations and situations that are coded in vPython are extremely difficult to make a functioning model of in real life.
For instance, the picture below is an example of program that was programmed to show the orbit of a craft around Earth.
This picture shows a graph that tracks.
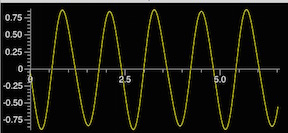
Examples
Simple:
Creating Shapes:
Sphere:
sphere= sphere(pos=vector(-4,-2,5), radius=.4, color=color.red)
Arrow:
bt=arrow(pos=sphere.pos, axis=sphere2.pos-sphere.pos, color=color.cyan)
Vector:
vector=vector(0, 0, 0)
Trail:
trail = curve(color=sphere.color) trail.append(pos=sphere.pos)
Setting Scene Range:
scene.range=11*sphere.radius
Helix:
spring = helix(pos=ceiling.pos, color=color.cyan, thickness=.003, coils=40, radius=0.015)
Intermediate:
Graphs:
Setup graphing windows:
gdisplay(width=500, height=250, x=600, y=1) ygraph = gcurve(color=color.yellow) gdisplay(width=500, height=250, x=600, y=300)
Plotting:
pgraph = gcurve(color=color.blue) ygraph.plot(pos=(time, Fnet.y)) pgraph.plot(pos=(time, sphere.y))
Difficult:
Using Loops to update Equations:
Constants:
G = ?
mEarth = ?
mmoon = ?
mcraft = ?
deltat = ?
t = ?
Objects and initial values:
Earth = sphere(pos=vector(0,0,0), radius=6.4e6, color=color.cyan) scene.range=11*Earth.radius Moon = sphere(pos=(4e8, 0, 0), radius=1.75e6, color=color.white)
Add a radius for the spacecraft. It should be BIG, so it can be seen:
craft = sphere(pos=vector(-6.656e7,-3.648e6,0), radius= 10000, color=color.yellow) vcraft = vector(206, 2645,0) pcraft = mcraft*vcraft pArrow=arrow(color=color.green) fArrow=arrow(color=color.cyan) dpArrow=arrow(color=color.red) Fnet_tangent_arrow = arrow(color=color.yellow) Fnet_perp_arrow= arrow(color=color.magenta)
This creates a trail for the spacecraft:
trail = curve(color=craft.color)
And this prevents zooming in or out:
scene.autoscale = 0
pscale=Earth.radius/mag(pcraft)
fscale=Earth.radius/((G*mEarth*mcraft)*mag(craft.pos-Earth.pos)**2)
dpscale=500*Earth.radius/mag(pcraft)
print("p=", pcraft)
Calculations:
Sets time for loop to run:
while t < 165240:
This slows down the animation (runs faster with bigger number):
rate(10000)
Add statements here for the iterative update of gravitational force, momentum, and position.
r = craft.pos-Earth.pos rmag = sqrt(r.x**(2)+r.y**(2)+r.z**(2)) Fmag= G*mEarth*mcraft/(rmag**2) rhat= r/rmag rmoon= craft.pos - Moon.pos rmoonmag= mag(rmoon) rmoonhat= norm(rmoon) Fmoonmag= G*mmoon*mcraft/(rmoonmag**2) Fmoon= -Fmoonmag*rmoonhat p_init= mag(pcraft) pcraft_i=pcraft+vector(0,0,0) Fearth= -Fmag*rhat Fnet= Fearth + Fmoon pcraft=Fnet*deltat+pcraft p_final=mag(pcraft)
Fnet_tangent = (p_final-p_init)*norm(pcraft)/deltat Fnet_tangent_arrow.pos=craft.pos Fnet_tangent_arrow.axis=Fnet_tangent*fscale Fnet_perp = Fnet-Fnet_tangent Fnet_perp_arrow.pos=craft.pos Fnet_perp_arrow.axis=Fnet_perp*fscale vcraft=pcraft/mcraft craft.pos=vcraft*deltat+craft.pos pArrow.pos=craft.pos pArrow.axis=pcraft*pscale fArrow.pos=craft.pos fArrow.axis=Fnet*fscale deltap= pcraft-pcraft_i dpArrow.pos=craft.pos dpArrow.axis=deltap*dpscale scene.center=craft.pos scene.range=craft.radius*600 Uncomment these two lines to exit the loop if the spacecraft crashes onto the Earth.
if rmag < Earth.radius:
break
trail.append(pos=craft.pos) t = t+deltat
