Tension

Chang Xu (Fall 2017)

This topic covers Tension.

Main Idea

What is Tension?

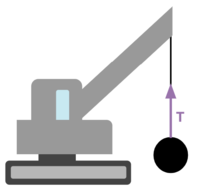
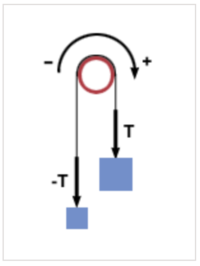
Tension is the force exerted by a rope (or anything that can be used to hang another object) on the object that is hanging from it. Usually, it is ropes and cables that have the tension force. In general, anything that is flexible can pull an object and have tension force. In consequence, the tension force can only be a pulling force. The rope will eventually go slack if someone tries to push with a rope, and it will act like just an object. Later we will see that this concept will help with draing force diagrams with the force of tension always pulling the object.

Tension is considered a contact force which means that the force is exerted when objects are touching. Usually, the force of tension is the force that is transmitted through a rope. If someone is pulling on a block with a rope, the person exerting force on the rope which transmits that force to the block. In problems, the ropes and cables will usually be massless, which perfectly transfers the force.

Mathematical Modeling

When calculating for tension force, tension force should be treated as one of the forces that is in the problem. The most important formula that will be used in this will be:

Fnet = Mass x Acceleration

This is based on Newton's Second Law, which applies because there will be multiple forces acting on the object so the forces must be added together. Because of this, we will also have to add all the forces together to find Fnet:

Fnet = F1 + F2 + ... + Fn for n number of forces.

A lot of times for simple force of tension problems, the acceleration may be 0, which causes our Fnet to be 0 (because Fnet = Mass x Acceleration). Acknowledging this will make calculating forces easier. This case will have to do with Newton's Third Law which sates that every force has an equal and opposite force; therefore, Fnet will be 0.

When acceleration is not 0, we will have to solve for Fnet and then for Ft (force of tension).

How To Calculate Tension Force

Because most situations of tension are different, there is no set way of calculating the force of tension. There are two situations in which we need to consider: zero acceleration and nonzero acceleration. Both will need the same steps, but zero acceleration will be easier to understand at first.

Tension Force with Zero Acceleration

1. Draw a free body diagram

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

The force of tension is shown by "T". There seems to be two forces of tension but they are actually the same magnitude because they come from the same string.

Whenever there is a question that has anything to do with force, the best thing to do first is to draw a free body diagram. This will help visualize the situation so you can see exactly where the forces will go. Common mistakes for force questions is that the direction of forces are wrong, so the student's solution turns out to be wrong. When drawing a free body diagram, make sure that the forces are all drawn in the right direction. Common forces to keep in mind when doing force of tension questions are:

• Ft = Force of Tension
• Fg = Force of Gravity
• Ff = Force of Friction
• Fn = Normal Force

1. Write equations that solve for Fnet

Because Fnet is 0 in this case because acceleration is 0, all the forces should add up to be 0. Make sure that the forces that are going in negative directions are negative. What could make this process easier is if you treat every force as the magnitude of the force and then add the magnitudes of the positive forces and subtract the magnitudes of the negative forces. That way, the negative signs will not get confused. Generally the equation would look like:

Fnet = 0 = F1 + F2 + ... + Fn (and then any other applied forces if there are any)

In this equation, the forces are not treated as magnitudes because the directions are not known. It is best to keep in note that the force of friction is usually going against velocity, and the force of gravity is usually pointing down in the y direction.

1. Solve for Ft

Once you have the equation done, it is possible to plug in forces to get to the solution for force of tension. If the problem does not give direct forces, here are some calculations of the forces:

• Fg = mg
• Ff = μFn
• Fn is perpendicular to the surface of the object

Example Problems

Example 1: Angled rope pulling on a box

A 2.0kg box of toy box is being pulled across a table by a rope at an angle θ=60º as seen below (ignore friction). The tension in the rope causes the box to slide across the table to the right with an acceleration of 3.0 m/s^2

What is the tension in the rope?

First draw a force diagram of all the forces acting on the box.

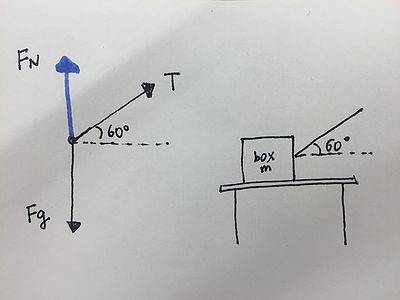
Now use Newton's second law. The tension is directed both vertically and horizontally, so it's a little unclear which direction to choose. However, since the acceleration is going horizontally, and since the tension is the only force directed horizontally, use Newton's second law in the horizontal direction.

1. a= ​ΣF/m (use Newtons's second law for the horizontal direction)
2. 3.0 m/s^2=Tcos60º/2.0kg ​​ (plug in the horizontal acceleration, mass, and horizontal forces)
3. Tcos60º=(3.0 m/s^2)(2.0kg)
4. T=[(3.0 m/s^2)(2.0kg)]/(cos60º)
5. T=12N

Example 2: Box hanging from two ropes

A 0.25 kg container hangs at rest from two strings secured to the ceiling and wall respectively. The diagonal rope under tension T1 is directed at an angle θ=30º from the horizontal direction as seen below.

What are the tensions (T1 and T2) in the two strings?

First draw a force diagram of all the forces acting on the container.

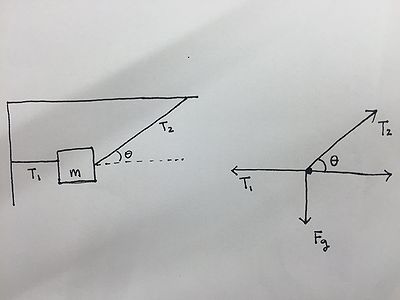
Now use Newton's second law. There are tensions directed both vertically and horizontally, so again it's a little unclear which direction to choose. However, since there is force of gravity (a vertical force), start with Newton's second law in the vertical direction.

1. a=​ΣF/m (use Newton's second law for the vertical direction)
2. 0=(T2*sin30º-Fg)/0.25kg
3. T2=Fg/(sin30º)
4. T2=mg/(sin30º)
5. T2=[(0.25kg)(9.8m/s²)]/(sin30º)
6. T2=4.9N

Now that we know T2 we can solve for the tension T1 using Newton's second law for the horizontal direction.

1. a=​ΣF/m (use Newton's second law for the horizontal direction)
2. 0=(T2*cos30º-T1)/0.25kg (plug in the horizontal acceleration, mass, and horizontal forces)
3. T1=T2*cos30º
4. T1=(4.9N)*cos30º
5. T1=4.2N

​

Connectedness

1. How is this topic connected to something that you are interested in?

When I was little, I went to a department store and I saw a transparent elevator. I never knew how elevator operated but through the transparent elevator, I realized that the pulling force of the ropes was what was keeping the elevator moving. This pulling force is tension and I later realized that this tension force is evident everywhere in my daily life.

1. How is it connected to your major?

I am not exactly sure how tension is connected to industrial engineering, which is my major. However, I can say that tension is a very basic concept in physics related to force and it is important to understand physics mechanism in studying industrial engineering.

1. Is there an interesting industrial application?

Tension force can be seen in everyday life, just like the elevator example I mentioned above. Tension force is applied when I pull a clothing tags.

See also

1. Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

I think it will be interesting to make connection between tension force and friction. Use both tension and friction in pulling a box in ice skating environment and concrete environment. This would be a good example to explore more about the topic.

Further reading

Books, Articles or other print media on this topic

Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. Hoboken, NJ: John Wiley & Sons, 2015. Print.

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page

Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. Hoboken, NJ: John Wiley & Sons, 2015. Print. https://www.khanacademy.org/science/physics/forces-newtons-laws/tension-tutorial/a/what-is-tension http://www.physicsclassroom.com/Class/newtlaws/U2L2b.cfm#tension http://hyperphysics.phy-astr.gsu.edu/hbase/mlif.html http://hyperphysics.phy-astr.gsu.edu/hbase/elev.html http://www.softschools.com/formulas/physics/tension_formula/70/ http://physics.stackexchange.com/questions/36175/understanding-tension http://www.brightstorm.com/science/physics/newtons-laws-of-motion/tension/