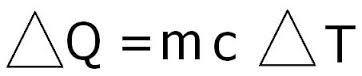Revision as of 19:01, 29 November 2017

by Dejan Tojcic

Improved by Gabriel Weese, Fall 2017

Specific Heat Capacity

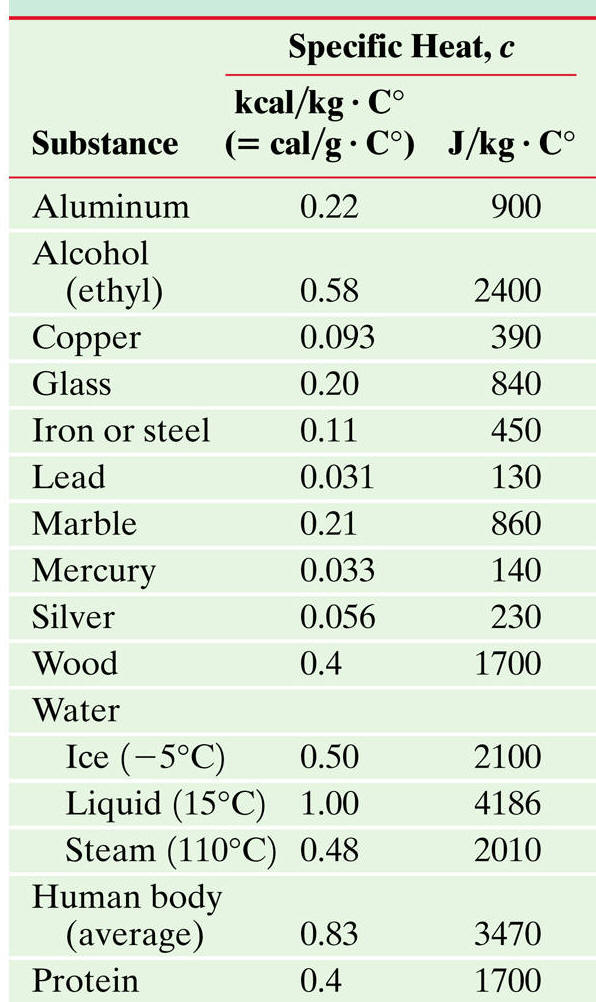
Specific Heat Capacity is simply a physical quantity that represents the ratio of the amount of heat taken or added to substance or object which results in a temperature change. The formal definition of Specific Heat is the amount of heat required to raise the temperature of 1 gram of a substance 1°C. The Standard Unit(SI) of this quantity is, joule per celsius per kilogram or or [math]\displaystyle{ \mathrm{\tfrac{J}{°C*Kg}} }[/math]. At the core, Specific Heat Capacity is based on the idea that different materials will store heat differently. The more formal definition states that different objects/substances have different specific heat capacities because every object has a varying mass, molecular structure, and numbers of particles per unit mass specific, and since specific heat capacity is reliant on mass, every different object has a different specific heat capacity.

Specific heat capacity additionally relates to Thermodynamics. Thermodynamics being the study of heat, energy, and temperature change of a system, with specific heat capacity directly impacting this.

A Mathematical Model

In order to find the Specific Heat Capacity of a substance, we use the equation:[math]\displaystyle{ \Delta E_{\mathrm{thermal}} = C * M * \Delta T }[/math], and rearrange it to get [math]\displaystyle{ C= \Delta E_{\mathrm{thermal}} /( M * \Delta T) . }[/math] where C is the Specific Heat Capacity with units of joules per celsius per kilogram or [math]\displaystyle{ \mathrm{\tfrac{J}{°C*Kg}} }[/math], M is the mass measured in kilograms or [math]\displaystyle{ \mathrm{kg} }[/math], [math]\displaystyle{ \Delta E_{\mathrm{thermal}} }[/math] represents the change in thermal energy measured by joules or [math]\displaystyle{ \mathrm{J} }[/math], and [math]\displaystyle{ \Delta T }[/math] represents change in temperature with units celsius or [math]\displaystyle{ \mathrm{°C.} }[/math]

It is important to note that another common variable used instead of [math]\displaystyle{ \Delta E_{\mathrm{thermal}} }[/math] is Q

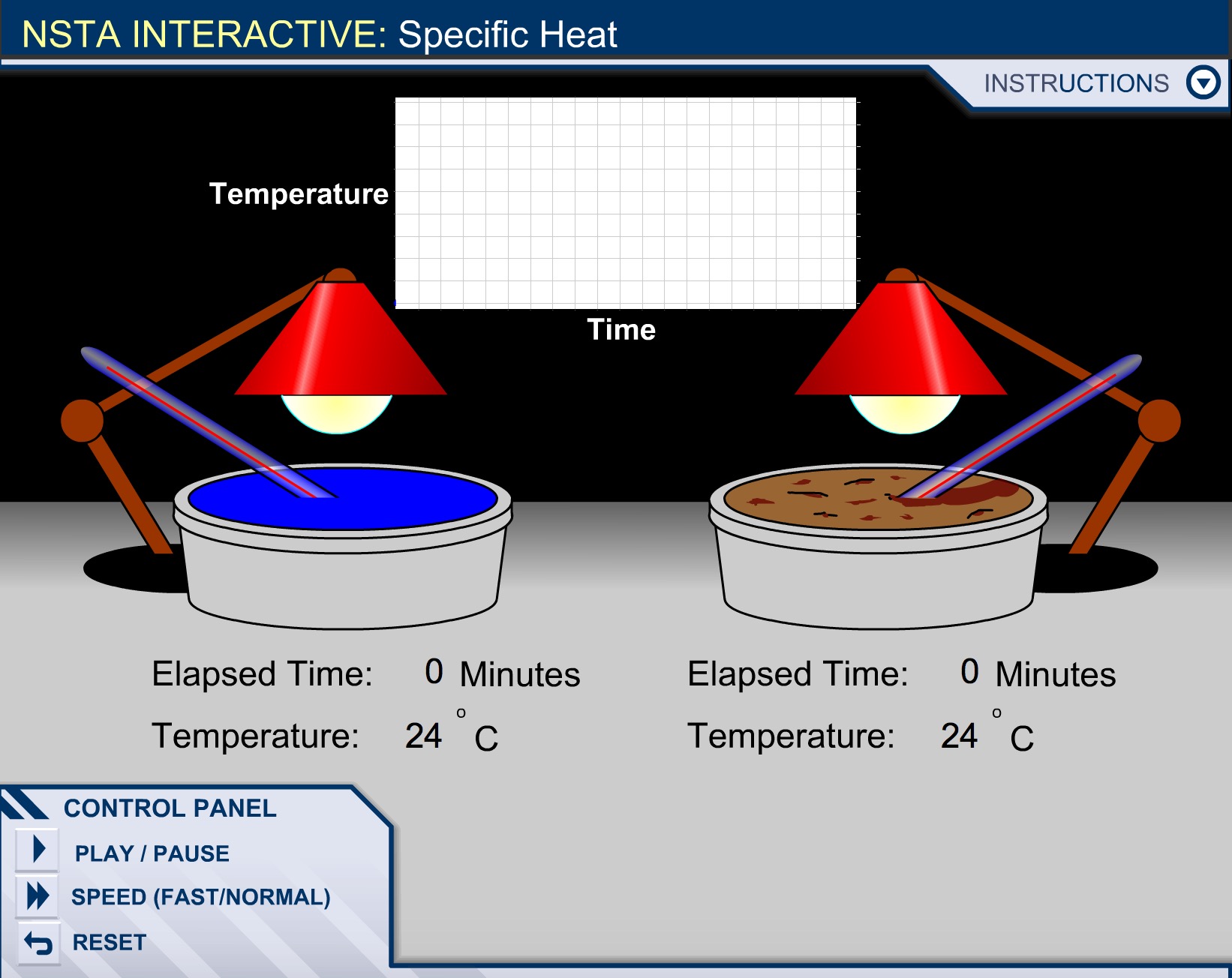
A Computational Model

While there is not really a way to depict specific heat capacity using python, here is an example of of interactive animation that displays the affects of specific heat capacity; with the link posted beneath the picture.

[1]

Simple Example

Question 
It takes 487.5 J to heat 25 grams of copper from 25 °C to 75 °C. What is the specific heat in Joules/g·°C?

Solution

This problem is very simplistic in nature as we are simply need to plug all of the values into the equation. Remembering the equation

All we have to do is rearrange it and solve for the specific heat capacity

Knowing that [math]\displaystyle{ \ Q }[/math] or [math]\displaystyle{ \Delta E_{\mathrm{thermal}} }[/math] is equal to the change in thermal energy, we can plug in 487.5 Joules into the equation, so now we have

[math]\displaystyle{ C= 487.5 joules /( M * \Delta T) . }[/math]

Next, looking at the question it looks like we are given the mass or [math]\displaystyle{ \mathrm{M} }[/math] which is 25 grams or . And can now plug that into the equation to get

[math]\displaystyle{ C= 487.5 joules /(25g * \Delta T) . }[/math]

Lastly, when we read the problem we see that we are given [math]\displaystyle{ \Delta T }[/math] which in this case would be [math]\displaystyle{ (75 °C-25 °C) }[/math] or [math]\displaystyle{ 50 °C }[/math]. We can finally solve for the value of [math]\displaystyle{ \mathrm{C} }[/math] which is

[math]\displaystyle{ C= 487.5 joules /( 25g * 50 °C) . }[/math]

and we finally conclude that

[math]\displaystyle{ C= .39{\tfrac{J}{g*°C}} }[/math] or the specific heat of copper is .39 J/(g*°C).

Question One morning while taking groceries out of your car, a 2.3 kg egg falls out of the carton and lands on the concrete. At this time, it has a temperature of 30C. 
You come back later and the temperature has raised to 63 degrees. Determine the change in thermal energy of the egg if the specific heat for the egg is (5.3 J/(gC))

This is a fairly straightforward question.

Using the equation for [math]\displaystyle{ \Delta E }[/math] We get:

[math]\displaystyle{ \Delta E = mC\Delta T }[/math]

We can substitute values in directly to get:

[math]\displaystyle{ \Delta E = (2.3 * 10^3 g)(5.3 J/(gC))(63C-30C) }[/math]

[math]\displaystyle{ \Delta E = 4.02 * 10^5 J }[/math]

Intermediate example

Question What is the final temperature when 625 grams of water at 75.0° C loses 7.96 x 10^4 J?

Solution While this problem may seem impossible at first glance, it really is not. It appears as if we are missing two constants,[math]\displaystyle{ \Delta T }[/math] and [math]\displaystyle{ C }[/math], or change in temperature and specific heat capacity. Water's specific heat capacity is almost "a universal constant" as it is noted for being the highest out of all substances with the value of 4.18 joules/(grams* °C). Now knowing the value [math]\displaystyle{ C=4.18{\tfrac{J}{°C*g}} }[/math], we see that the question is asking for [math]\displaystyle{ \Delta T }[/math], which is equal to [math]\displaystyle{ ( T_{\mathrm{initial}} - T_{\mathrm{final}}) }[/math].

We can again use the same equation as on this occasion we are solving for [math]\displaystyle{ \Delta T }[/math] or [math]\displaystyle{ ( T_{\mathrm{final}}) }[/math] more specifically, so we can rearrange it to get

[math]\displaystyle{ \Delta T= \Delta E_{\mathrm{thermal}}/( C * M) }[/math]

We can start plugging in variables now, so we know [math]\displaystyle{ \Delta E_{\mathrm{thermal}}=7.96 * 10^4 J }[/math], and we know this because in the problem it states "loses 7.96 x 10^4 J? Therefore the equation now looks like

[math]\displaystyle{ \Delta T= 7.96 x 10^4 J/( C * M) }[/math]

We can now plug in the mass of the water as in the problem it was given to be [math]\displaystyle{ M= 625 grams }[/math] as now the updated equation is

[math]\displaystyle{ \Delta T= 7.96 x 10^4 J/( C * 625 grams) }[/math]

Lastly, all we need to add to calculate [math]\displaystyle{ \Delta T }[/math] is ,[math]\displaystyle{ C }[/math], which is the specific heat capacity for water commonly known to equal [math]\displaystyle{ C=4.18{\tfrac{J}{°C*g}} }[/math].

[math]\displaystyle{ \Delta T= 7.96 x 10^4 J/( 4.18{\tfrac{J}{°C*g}} * 625 grams) }[/math]

We have finally solved the equation and determined that [math]\displaystyle{ \Delta T= 30.5°C }[/math]

However, if you look at the question, it asks for "final temperature" and not [math]\displaystyle{ \Delta T }[/math]. Thus in order to calculate the final temperature we must use the equation [math]\displaystyle{ \Delta T= T_{\mathrm{initial}} - T_{\mathrm{final}} }[/math] and rearrange it to solve for [math]\displaystyle{ T_{\mathrm{final}} }[/math] so that it looks like

[math]\displaystyle{ T_{\mathrm{final}}= T_{\mathrm{initial}}-\Delta T }[/math]

And since the quantities [math]\displaystyle{ T_{\mathrm{initial}}= 75.0°C }[/math] and [math]\displaystyle{ \Delta T= 30.5°C }[/math] are known, we simply plug these into the formula to compute [math]\displaystyle{ T_{\mathrm{final}} }[/math]

[math]\displaystyle{ T_{\mathrm{final}}= 75.0°C- 30.5°C }[/math]

So we finally determine that [math]\displaystyle{ T_{\mathrm{final}}= 44.5°C }[/math].

Hard Example

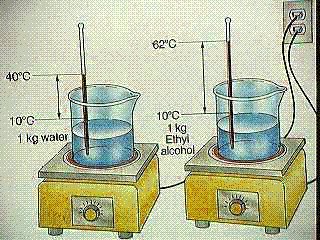
Question Calculate the specific heat of ethyl alcohol using the diagram

Analyze the problem: You need to look into the diagram pretty deeply before you attempt to to solve the problem. The question directly states that it is looking for the specific heat of the ethyl alcohol, but that is all it says so we will need to analyze the diagram itself.

Looking at the diagram we can see that there is 1 kilograms or 1000 grams of ethyl alcohol, so we know [math]\displaystyle{ M{\mathrm{ethyl alcohol}}= 1000grams }[/math] . Next when solving for [math]\displaystyle{ \Delta T_{\mathrm{ethyl alcoholl}} }[/math] we can see in the diagram that they give us the initial temperature of [math]\displaystyle{ T_{\mathrm{initial}}= 10°C }[/math] and the final temperature of [math]\displaystyle{ T_{\mathrm{final}}= 62°C }[/math]. Therefore we can use the equation

[math]\displaystyle{ \Delta T= T_{\mathrm{final}} - T_{\mathrm{intial}} }[/math] , to get

[math]\displaystyle{ \Delta T_{\mathrm{ethyl alcohol}}= 62°C-10°C = 52°C }[/math] And we conclude that the change in temperature or [math]\displaystyle{ \Delta T_{\mathrm{ethyl alcohol}}= 52°C }[/math]

Now it appears as we have identified all the known values of ethyl alcohol, so now lets move on to the water.

We can start of by identifying that the specific heat capacity of water or [math]\displaystyle{ C_{\mathrm{water}}= 4.18{\tfrac{J}{°C*g}} }[/math] and this is known as we identified it to be a universal constant.

Looking at the diagram we can see that there is 1 kilograms or 1000 grams of water , so we know [math]\displaystyle{ M_{\mathrm{water}}= 1000grams }[/math] .

Next when solving for [math]\displaystyle{ \Delta T_{\mathrm{water}} }[/math] we can see in the diagram that they give us the initial temperature of [math]\displaystyle{ T_{\mathrm{initial}}= 10°C }[/math] and the final temperature of [math]\displaystyle{ T_{\mathrm{final}}= 40°C }[/math]. Therefore we can use the equation

[math]\displaystyle{ \Delta T= T_{\mathrm{final}} - T_{\mathrm{intial}} }[/math] , to get

[math]\displaystyle{ \Delta T_{\mathrm{water}}= 40°C-10°C = 30°C }[/math] And we conclude that the change in temperature or [math]\displaystyle{ \Delta T_{\mathrm{water}}= 30°C }[/math]

Now it appears that we have identified all the known values, however it seems as if we are missing [math]\displaystyle{ \Delta E_{\mathrm{ethyl alcoholl}} }[/math],[math]\displaystyle{ \Delta E_{\mathrm{water}} }[/math], and [math]\displaystyle{ C_{\mathrm{ethyl alcohol}} }[/math] , but if we examine the picture of the problem again closely

We can determine that both bunsen burners are set at equal settings,so the [math]\displaystyle{ \Delta E }[/math] or heat added to both substances is the same. Therefore, we can cancel this out which will give us the resulting equation

[math]\displaystyle{ C{\mathrm{ethyl alcohol}} * M{\mathrm{ethyl alcohol}} * \Delta T{\mathrm{ethyl alcohol}}= C{\mathrm{water}} * M{\mathrm{water}} * \Delta T{\mathrm{water}} }[/math]

And we can simply this equation to solve for [math]\displaystyle{ C_{\mathrm{ethyl alcohol}} }[/math]

[math]\displaystyle{ C{\mathrm{ethyl alcohol}}=( C{\mathrm{water}} * M{\mathrm{water}} * \Delta T{\mathrm{water}} )/ (M{\mathrm{ethyl alcohol}} * \Delta T{\mathrm{ethyl alcohol}} }[/math])

[math]\displaystyle{ C{\mathrm{ethyl alcohol}}=( 4.18{\tfrac{J}{°C*g}}*1000g*30°C)/(1000g*52°C) }[/math]

And finally we determine that the specific heat of ethyl alcohol or [math]\displaystyle{ C{\mathrm{ethyl alcohol}}= 2.4{\tfrac{J}{°C*g}} }[/math].

Question: Prof. Parker takes 2.1 kg of 102 C eggs with a specific heat capacity of 4.2 J/(g*C), and places .7 kg of cheese on top. The cheese has temperature 5 C, and specific heat of 3.6 J/(g*C). 
Assuming the eggs + cheese are a closed system, calculate the final equilibrium temperature for the system.

To start this problem, we analyze the situation presented. Our system consists of the Eggs and the cheese. We know from the problem that our system is closed, so we will have no change in thermal energy. It is also important to note that the final temperature for both objects will be the same, because the system reaches equilibrium.

Starting with the energy principle gives us the following:

[math]\displaystyle{ \Delta E_{\mathrm{sys}}= \Delta E_{\mathrm{eggs}} + \Delta E_{\mathrm{cheese}} }[/math]

Because we know that our change in the system is equal to zero, we can rewrite the equation as follows:

[math]\displaystyle{ \Delta E_{\mathrm{eggs}} + \Delta E_{\mathrm{cheese}}=0 }[/math]

At this point, we take a look at the composition of [math]\displaystyle{ \Delta E_{\mathrm{eggs}} }[/math] and [math]\displaystyle{ \Delta E_{\mathrm{cheese}} }[/math]

Using the definition of specific heat capacity, we know that the change in energy of a particular component is as follows:

[math]\displaystyle{ \Delta E= mC\Delta T }[/math]

We are going to expand out change in temperature because that will allow us to solve for final temperature.

[math]\displaystyle{ \Delta E_{\mathrm{eggs}}= m_{\mathrm{eggs}}c_{\mathrm{eggs}} (T_{\mathrm{final}} - T_{\mathrm{intialeggs}}) }[/math]

We can use the same equation to calculate the change in energy of cheese.

[math]\displaystyle{ \Delta E_{\mathrm{cheese}}= m_{\mathrm{cheese}}c_{\mathrm{cheese}} (T_{\mathrm{final}} - T_{\mathrm{intialcheese}}) }[/math]

Now that we have these two equations, we can substitute them for [math]\displaystyle{ \Delta E_{\mathrm{eggs}} and \Delta E_{\mathrm{cheese}} }[/math]

This gives us:

[math]\displaystyle{ m_{\mathrm{eggs}}c_{\mathrm{eggs}} (T_{\mathrm{final}} - T_{\mathrm{intialeggs}}) + m_{\mathrm{cheese}}c_{\mathrm{cheese}} (T_{\mathrm{final}} - T_{\mathrm{intialcheese}}) = 0 }[/math]

Distributing gives us:

[math]\displaystyle{ m_{\mathrm{eggs}}c_{\mathrm{eggs}}T_{\mathrm{final}} - m_{\mathrm{eggs}}c_{\mathrm{eggs}}T_{\mathrm{intialeggs}} + m_{\mathrm{cheese}}c_{\mathrm{cheese}}T_{\mathrm{final}} - m_{\mathrm{cheese}}c_{\mathrm{cheese}}T_{\mathrm{intialcheese}} = 0 }[/math]

Factoring out final temperature gives us :

[math]\displaystyle{ T_{\mathrm{final}}( m_{\mathrm{eggs}}c_{\mathrm{eggs}}+ m_{\mathrm{cheese}}c_{\mathrm{cheese}}) = m_{\mathrm{eggs}}c_{\mathrm{eggs}}T_{\mathrm{intialeggs}}+m_{\mathrm{cheese}}c_{\mathrm{cheese}}T_{\mathrm{intialcheese}} }[/math]

Solving for final T gives us:

[math]\displaystyle{ T_{\mathrm{final}} = (m_{\mathrm{eggs}}c_{\mathrm{eggs}}T_{\mathrm{intialeggs}}+m_{\mathrm{cheese}}c_{\mathrm{cheese}}T_{\mathrm{intialcheese}})/( m_{\mathrm{eggs}}c_{\mathrm{eggs}}+ m_{\mathrm{cheese}}c_{\mathrm{cheese}}) }[/math]

Plugging in numbers given will give us:

[math]\displaystyle{ T_{\mathrm{final}}= ((2.1* 10^3g)(4.2J/(gc))(102C)+(.7*10^3g)(3.6J/(gc))(5C))/((2.1*10^3g)(4.2J/(gC))+(.7*10^3g)(3.6J/(gC))) }[/math]

[math]\displaystyle{ T_{\mathrm{final}} = 80.4C }[/math]

Connectedness

It is easy to notice that water's specific heat capacity is much larger than anything else, but why? The answer is due to water's intermolecular forces. Since a water molecule is made up from one oxygen atom(negative charge) and two hydrogen atoms(slight positive charges), water has hydrogen bonds which result in the "sticking" of water molecules. Because of these hydrogen bonds it requires a lot of energy to heat up water molecules, because not only do you have to use energy to increasing the movement of the particle, but also to break the hydrogen bonds. As a result water has a high specific heat capacity because it takes a lot of energy to break the hydrogen bonds.

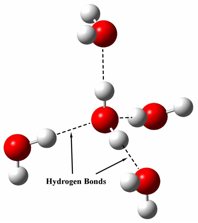(illustration of the hydrogen bonds in water)

But why is this important?

A large body of water can absorb and store a huge amount of heat from the sun in the daytime and during summer while warming up only a few degrees. And at night and during winter, the gradually cooling water can warm the air. This is the reason coastal areas generally have milder climates than inland rtegions. The high specific heat of water also tends to stabilize ocean temperatures, creating a favorable environment for marine life. THus because of its high specific heat, the water that covers most of Earth keeps temperature fluctuations on land and in water within limits that permit life. Also, because organisms are primarily made of water, they are more able to resist changes in their own temperature than if they were made of a liquid with a lower specific heat.

History

Dr. Joseph Black, of the University of Glasgow, was first credited with developing the concept of latent heat and specific heat in the mid 18th century, and this really allowed the study of Thermodynamics to be further looked in to. Before specific heat capacity was known, scientists referred to heat as some sort of invisible liquid; however, after the establishment of the idea of specific heat capacity and latent heat, scientists began to think of heat as a systems change in internal energy. This is very important as the concept of specific heat has helped lead to the vast development of the field of thermodynamics.