Problem Solving: Difference between revisions
| Line 6: | Line 6: | ||
[[File:Graph_representation.png|500px|thumb|center|Graph representation of a circuit]] | [[File:Graph_representation.png|500px|thumb|center|Graph representation of a circuit]] | ||
===Incidence Matrix=== | ===Incidence Matrix=== | ||
| Line 14: | Line 13: | ||
[[File:Incidence_matrix.jpg|350px|thumb|center|Incidence matrix of a sample graph.<ref>{{Citation|last=Strang|first=Gilbert|date=July 19, 2016|title=Introduction to Linear Algebra|publisher=Wellesley-Cambridge Press|edition=5th|isbn=978-0-9802327-7-6}}</ref> | [[File:Incidence_matrix.jpg|350px|thumb|center|Incidence matrix of a sample graph.<ref>{{Citation|last=Strang|first=Gilbert|date=July 19, 2016|title=Introduction to Linear Algebra|publisher=Wellesley-Cambridge Press|edition=5th|isbn=978-0-9802327-7-6}}</ref> | ||
]] | ]] | ||
Here, <math>x_{1}, x_{2}, x_{3} and x_{4}</math> represent the voltages at the nodes. Then <math>A\vec{x}_{edge} = x_{end} - x_{start}</math> gives the voltage differences <math>∆V</math>. | |||
===Loop Rule (Kirchhoff's voltage law)=== | ===Loop Rule (Kirchhoff's voltage law)=== | ||
Revision as of 20:14, 29 November 2017
Linear algebra can be used to solve large ohmic circuits. This page explains how to define the circuit problem in terms of a linear system that can be solved with computational methods like matlab or python.
The Main Idea
We can describe an electrical circuit as a graph where the nodes represent specific points and the edges represent the components connecting them. E.g:
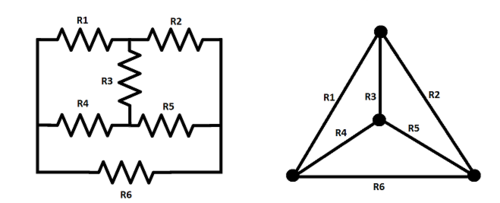
Incidence Matrix
The incidence matrix, A, is a matrix of dimensions m x n, where m is the number of edges and n is the number of nodes. If x is the vector that contains all the nodes in order, A satisfies: [math]\displaystyle{ A\vec{x}_{edge} = x_{end} - x_{start} }[/math] Thus, the resulting matrix will have zeros in every element of each row, except for the start and the end nodes, which will be -1 and 1 respectively:
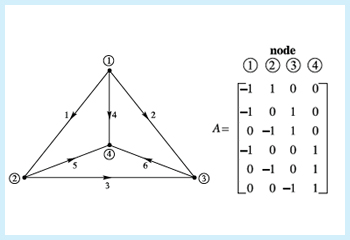
Here, [math]\displaystyle{ x_{1}, x_{2}, x_{3} and x_{4} }[/math] represent the voltages at the nodes. Then [math]\displaystyle{ A\vec{x}_{edge} = x_{end} - x_{start} }[/math] gives the voltage differences [math]\displaystyle{ ∆V }[/math].
Loop Rule (Kirchhoff's voltage law)
Using this creative way of transforming a circuit to a graph and getting the incidence matrix from it allows us to do some interesting things. Kirchhoff's loop rule is a principle of conservation of energy that implies that the directed sum of the voltage differences around any closed network is zero.
This means that the components of [math]\displaystyle{ A\vec{x} = b }[/math] add to zero around every loop. Moreover, the voltage law can decide whether b is in the column space of A.
We know from Ohm's law that [math]\displaystyle{ V = I * R }[/math]. Then, in the previous graph for example, we would have that [math]\displaystyle{ V_{edge1} = I * R = (direction) * R_{1} = 1 * R_{1} }[/math].
Kirchhoff's Current Law
A Mathematical Model
What are the mathematical equations that allow us to model this topic. For example [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net} }[/math] where p is the momentum of the system and F is the net force from the surroundings.
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
<references>