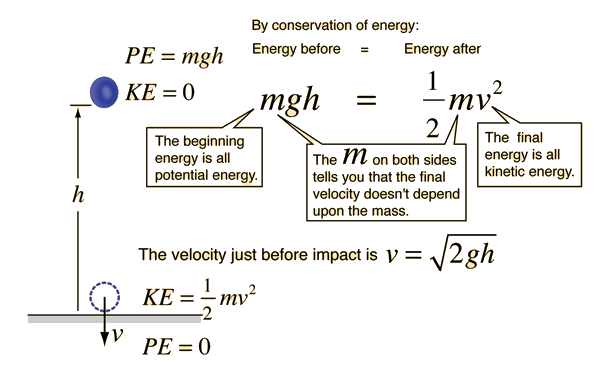Conservation of Energy: Difference between revisions

Revision as of 22:10, 18 April 2018

Alex Reyna claimed 4/18/2018

This page was originally created by ksubramanian33, as can be seen by the edit history.

Main Ideas

Conceptual Model

The law of conservation of energy states that the total amount of energy of a system before and after an interaction between objects.
This only applies to isolated systems (no outside forces acting on the system).
- Not Isolated: An object sliding across a rough floor (system = the object). There is work being done by the floor on the object because of the frictional force. Energy lost to heat due to friction is an example of mechanical energy being converted into thermal energy.
- Isolated: An object sliding across a rough floor (system = the object AND the floor). There is no work done on the system because all the forces are contained in the system.

see reference 7

see reference 3

Mathematical Model

Single Particle
- Particle Energy: E_particle = γmc²
- Rest Energy: E_rest = mc²
- Kinetic (particle): K = γmc² + mc²
General Objects
- Kinetic: (1/2)mv²
- Gravitational Potential: (-Gm₁m₂)/(R²) (large distances), mgh (near the surface of the Earth)
- Spring (Elastic) Potential: (1/2)k_ss²
- Thermal Energy: mCΔT

General Formulas

E = W + Q (if no heat transfer indicated, Q = 0; if no external forces acting on system, W = 0)
E = K + U (The total energy is the sum of the kinetic and potential energies. From this, you can infer that for an isolated system, any change in kinetic energy will correspond in an equal but opposite change in the potential energy and vice versa.)

These formulas can be interchanged. For example, if you know work and heat transfer are zero, energy equals zero, so K + U will equal zero

See Reference 2

Basic Explanation of Conservation of Energy
Skater Visualization of Transfers of Energy

Computational Model

Below is a link to a segment of Vpython code that models the motion of a spring and graphs its kinetic and potential energy. It also shows how the total amount of energy of the system does not change.

"https://trinket.io/embed/glowscript/49c1365501?showInstructions=true"

Examples

Particle

An electron is accelerated to a speed of 2.95 × 10⁸ 

(a) What is the energy of the electron? 

(b) What is the rest energy of the electron? 

(c) What is the kinetic energy of the moving proton?

(a)
E = γmc²
E = (5.50)(9.11 × 10^-31)(3 × 10⁸)
E = 1.50 × 10^-21 J
(b)
E_rest = mc²
E_rest = (9.11 × 10^-31)(3 × 10⁸)²
E_rest = 2.73 × 10^-22 J
(c)
K = E - E_rest
K = 1.50 × 10^-21 - 2.73 × 10^-22
K = 1.23 × 10^-21 J

Simple

A ball is at rest on a table with 50 J of potential energy. 
It then rolls of the table, and at one point in time as it falls, the ball has 30 J of kinetic energy.

What is the potential energy of the ball at that instant?

See Reference 3

E_initial = E_final
K_initial + U_initial = K_final + U_final
0 J + 50 J = 30 J + U_final
U_final = 20 J

Middling

A ball is at rest 50 m above the ground. You then drop the ball.
What is its speed before hitting the ground?

See Reference 4

v = √2gh
v = √2(9.8)(50)
v = 31.3 m/s

Difficult

The driver of an SUV (m = 1700 kg) isn’t paying attention and rear ends a car (m = 950 kg) on level ground at a red light.
On impact, both drivers lock their brakes. The SUV and car stick together and travel a distance of 8.2 m before they
come to a stop. How fast was the SUV traveling just before the collision? The coefficient of friction between the tires and
the road is 0.72.

See Reference 5

KE₂ + PE₂ = KE₃ + PE₃ - W_nc
(1/2)m_totalv₂² + m_totalgh₂ = (1/2)m_totalv₃² + m_totalgh₃ - W_nc
(1/2)m_totalv₂² + 0 = 0 + 0 - (μm_totalg)dcos(180°)
(1/2)v₂² = -(0.72)(9.8 m/s²)(8.2 m)(-1)
v₂² = 116 m²/s²
v₂ = 10.8 m/s

Notice how the mass is canceled.

p₁ = p₂
p_1x = p_2x
m_suvv_suv + m_carv_car = m_totalv₂
(1700 kg)v_suv + 0 = (2650 kg)(10.8 m/s)
(1700 kg)v_suv = 28600 kgm/s
v_suv = 17 m/s

Connectedness

Industrial Engineering
1. How is this topic connected to something that you are interested in?
This concept is clearly connected to physics and helps explain and sometimes predict how objects transform and change as a result of different interactions. Knowing why and how things move and interact is very powerful.
2. How is it connected to your major?
This topic is connected to industrial engineering as the field deals heavily with optimization of production processes im manufacturing environments. Obviously, modeling and simulating industrial processes at its core uses the fundamental principles of physics. It is important to take all fundamental concepts of physics, including the conservation of energy, into account.
3. Is there an interesting industrial application?
The law of conservation of energy is prevalent in nearly every industrial application of physics. More specifically, it is relevant today as finding renewable and sustainable forms of energy is becoming a more prevalent social and economic issue. It will be interesting to see how this concept will be applied as we try to get more energy for less. Additionally, the law of conservation of energy can be applied at a nuclear microscopic level as radiating particles like alpha particles follow the same energy principle as objects on a macroscopic level.

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
Who: Many physicists contributed to the knowledge of energy, however it is most notably atributed to Julius Robert Mayer
What: Most formally discovered the law of conservation of energy
When: 1842
Where: Germany
Why: To explain what happens to energy in an isolated system
See Reference 6

@@ Line 111: / Line 111: @@
 ==Connectedness==
-<b>Computer Science</b><br>
+<b>Industrial Engineering</b><br>
 . How is this topic connected to something that you are interested in?<br>
-This concept is clearly connected to physics and helps explain and sometimes predict how our world works. Knowing why and how things move and interact is very powerful.  <br>
+This concept is clearly connected to physics and helps explain and sometimes predict how objects transform and change as a result of different interactions. Knowing why and how things move and interact is very powerful.  <br>
 . How is it connected to your major?<br>
-This topic is connected to computer science in the field of modeling and simulation. When you use computers to more efficiently model grand scale scenarios, it is important to take all fundamental concepts of physics, including the conservation of energy, into account.<br>
+This topic is connected to industrial engineering as the field deals heavily with optimization of production processes im manufacturing environments. Obviously, modeling and simulating industrial processes at its core uses the fundamental principles of physics. It is important to take all fundamental concepts of physics, including the conservation of energy, into account.<br>
 . Is there an interesting industrial application?<br>
-The law of conservation of energy is prevalent in nearly every industrial application of physics. More specifically, it is relevant today as finding renewable and sustainable forms of energy is becoming a more prevalent social and economic issue. It will be interesting to see how this concept will be applied as we try to get more energy for less.<br>
+The law of conservation of energy is prevalent in nearly every industrial application of physics. More specifically, it is relevant today as finding renewable and sustainable forms of energy is becoming a more prevalent social and economic issue. It will be interesting to see how this concept will be applied as we try to get more energy for less. Additionally, the law of conservation of energy can be applied at a nuclear microscopic level as radiating particles like alpha particles follow the same energy principle as objects on a macroscopic level.<br>
 ==History==