Acceleration

This page defines and describes acceleration.

The Main Idea

Acceleration is a vector quantity defined as the rate of change of velocity with respect to time:

[math]\displaystyle{ \mathbf{\vec{a}} = \frac{\Delta \vec{v}}{\Delta t}. }[/math]

Acceleration is a vector and has units of meters per second per second (m/s/s) or (m/s²).

This means that if acceleration is integrated, the result is velocity, and if velocity is integrated, the result is displacement.

A Mathematical Model

Instantaneous acceleration is defined as:

[math]\displaystyle{ \vec{a} = \lim_{{\Delta t}\to 0} \frac{\Delta \vec{v}}{\Delta t} = \frac{d\vec{v}}{dt} }[/math]

It is the limit of the average acceleration over an interval of time.

Derivative Relationships

Acceleration is also the derivative of velocity, if given a function, or the second derivative of displacement.

Recall that:

[math]\displaystyle{ \vec{a}(t) = \frac{d\vec{v}(t)}{dt} }[/math] and [math]\displaystyle{ \vec{v}(t) = \frac{d\vec{x}(t)}{dt} }[/math]

Therefore:

[math]\displaystyle{ \vec{a}(t) = \frac{d\vec{v}}{dt} = \frac{d^2\vec{r}}{dt^2} }[/math]

Integral Relationships

The integral of acceleration yields velocity, and the integral of velocity yields displacement.

Recall that:

[math]\displaystyle{ \vec{x}(t) = \int \vec{v}(t) \ dt }[/math] and [math]\displaystyle{ \vec{v}(t) = \int \vec{a}(t) \ dt }[/math]

Therefore:

[math]\displaystyle{ \vec{x}(t) = \iint \vec{a}(t) \, dt, dv }[/math]

Kinematics Equations

The kinematics equations can be derived from the derivative and integral relationships between acceleration, velocity, and displacement.

[math]\displaystyle{ \vec{v}_{f} = \vec{v}_{i}+{\vec{a}{\Delta t}} }[/math]

[math]\displaystyle{ \vec{v}^2_{f} = \vec{v}^2_{i}+ 2 {\vec{a}{\Delta x}} }[/math]

[math]\displaystyle{ \vec{x}_{f} = \vec{x}_{i}+{\vec{v}_{i}{t}}+ 1/2 {\vec{a}}{t}^2 }[/math]

Newton's Second Law of Motion

Force, as a vector quantity, equals mass times acceleration, as a vector.

Another form of acceleration is given by Newton's second law of motion:

[math]\displaystyle{ \vec{F} = m \vec{a} \quad \to \quad \vec{a} = \vec{F}/m }[/math]

where [math]\displaystyle{ \vec{F} }[/math] is the net force acting on the body, m is the mass of the body, and [math]\displaystyle{ \vec{a} }[/math] is the center-of-mass acceleration.

Why does [math]\displaystyle{ {\vec{F}}= m{\vec{a}} }[/math]?

This formula can easily be derived from Newton's Second Law: the Momentum Principle.

Recall that:

[math]\displaystyle{ {\Delta\vec{p}} = {\vec{F}_{net}{\Delta t}} }[/math] and [math]\displaystyle{ {\Delta\vec{p}} = m {\Delta\vec{v}} }[/math]

Therefore:

[math]\displaystyle{ {\vec{F}} = \frac{\Delta\vec{p}}{\Delta t} = \frac{m {\Delta\vec{v}}}{\Delta t} = m {\frac{\Delta\vec{v}}{\Delta t}} }[/math]

Note: [math]\displaystyle{ \vec{a} = \frac{\Delta\vec{v}}{\Delta t} }[/math]

Therefore:

[math]\displaystyle{ {\vec{F}} = \frac{\Delta\vec{p}}{\Delta t} = m\vec{a} }[/math]

A Graphical Model

Here are some examples to help you see acceleration graphically.

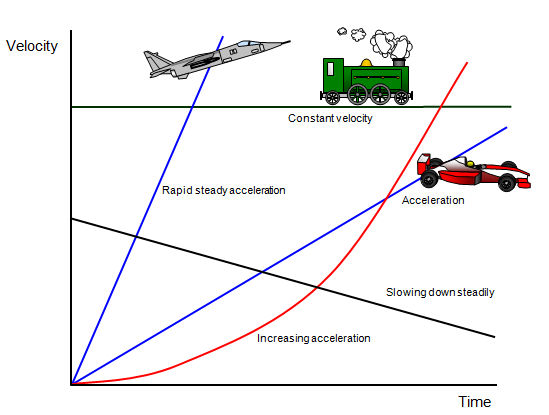
[Above] Here you can see many different graphs of velocity over time. Notice the difference between an increasing acceleration, constant velocity, and constant acceleration. The slope of the line on a velocity versus time graph is acceleration.

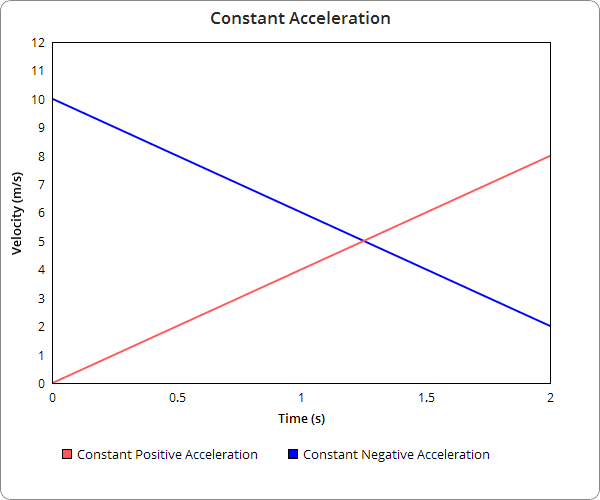
Constant Acceleration

Constant acceleration is shown with straight lines on velocity over time graphs. This means that the velocity is changing by a single constant amount per second. Positive slopes mean that the acceleration is positive, and this means the velocity is constantly increasing. Negative acceleration slopes denote a negative acceleration and decreasing velocity. Lines with zero slope have no acceleration and a constant velocity.

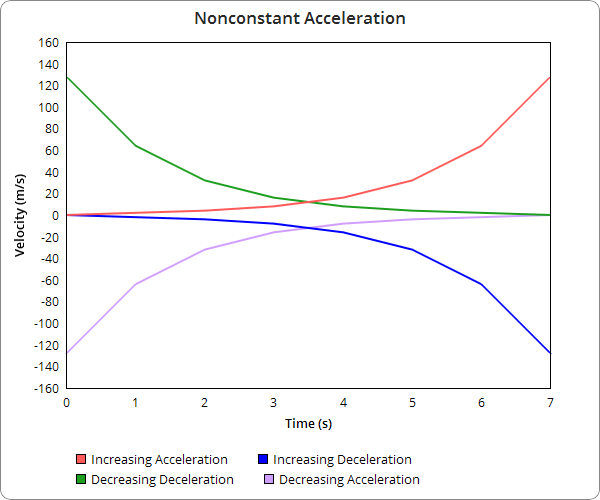
Nonconstant Acceleration

Nonconstant Acceleration is shown with curved lines on velocity over time graphs. Graphs that concave up and are increasing show increasing acceleration, and graphs that concave up and are decreasing show decreasing deceleration. Graphs that concave down and are increasing show decreasing acceleration and graphs that are concave down and decreasing show increasing deceleration.

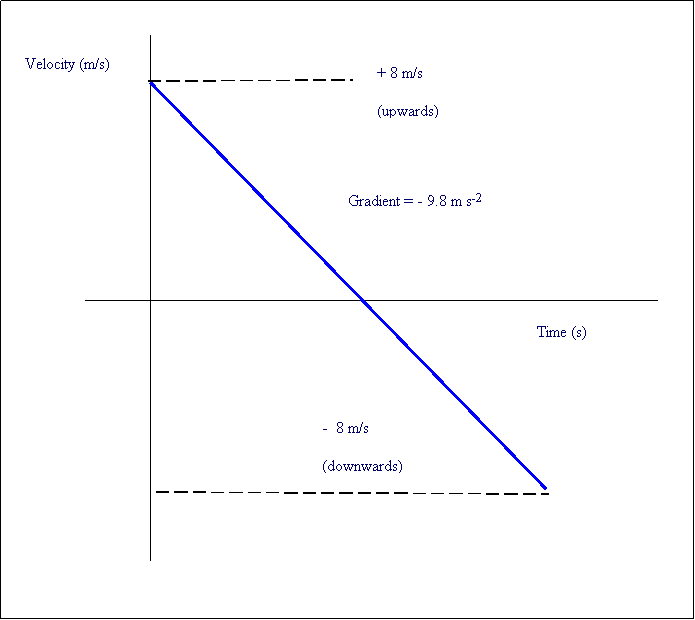
Example

[Above] Here is a common example showing the velocity of a ball being thrown into the air. Notice that the slope = -9.8 (acceleration due to gravity) and that the graph goes through the x-axis. (The crossover is when the ball is at the highest height and v = 0)

Examples

Here are a couple simple acceleration problems with solutions included:

Question 1

Question:

A motorcycle accelerates uniformly from rest to a speed of 7.10 m/s over a distance of 35.4 m. Determine the acceleration of the motorcycle.

Solution:

Given:

[math]\displaystyle{ v_i = 0 m/s }[/math]

[math]\displaystyle{ v_f = 7.10 m/s }[/math]

[math]\displaystyle{ d = 35.4 m }[/math]

Find:

[math]\displaystyle{ a = ? }[/math]

Calculations:

[math]\displaystyle{ v_f^2 = v_i^2 + 2ad }[/math]

[math]\displaystyle{ 2ad = v_f^2 - v_i^2 }[/math]

[math]\displaystyle{ a = \frac{v_f^2 - v_i^2}{2*d} }[/math]

[math]\displaystyle{ a = \frac{(7.10m/s)^2 - (0m/s)^2}{2*35.4m} }[/math]

[math]\displaystyle{ a = 0.712 m/s^2 }[/math]

Question 2

Question:

A rabbit can jump to a height of 2.62 m. Determine the takeoff speed of the rabbit.

Solution:

Given:

[math]\displaystyle{ a = -9.8 m/s^2 }[/math]

[math]\displaystyle{ v_f = 0 m/s }[/math] *Considering the moment of takeoff to maximum height

[math]\displaystyle{ d = 2.62 m }[/math]

Find:

[math]\displaystyle{ v_i = ? }[/math]

Calculations:

[math]\displaystyle{ v_f^2 = v_i^2 + 2ad }[/math]

[math]\displaystyle{ v_i^2 = 2ad - v_f^2 }[/math]

[math]\displaystyle{ v_i = \sqrt{2ad - v_f^2} }[/math]

[math]\displaystyle{ v_i = \sqrt{2*-9.8m/s^2*2.62m - (0m/s)^2} }[/math]

[math]\displaystyle{ v_i = 7.17 m/s }[/math]

Question 3

Question:

A rock is dropped into a lake and is heard to hit the water 3.41 s after being dropped. Determine the depth of the lake.

Solution:

Given:

[math]\displaystyle{ a = -9.8 m/s^2 }[/math]

[math]\displaystyle{ t = 3.41 s }[/math]

[math]\displaystyle{ v_i = 0 m/s }[/math]

Find:

[math]\displaystyle{ d = ? }[/math]

Calculations:

[math]\displaystyle{ d = v_i*t + 0.5*a*t^2 }[/math]

[math]\displaystyle{ d = (0 m/s)*(3.41 s)+ 0.5*(-9.8 m/s^2)*(3.41 s)^2 }[/math]

[math]\displaystyle{ d = 0 m + 0.5*(-9.8 m/s^2)*(11.63 s^2) }[/math]

[math]\displaystyle{ d = -57.0 m }[/math] (57.0 meters deep)

A Computational Model

https://trinket.io/embed/glowscript/569486a2bb