Iterative Prediction of Spring-Mass System

claimed by kgiles7

The Main Idea

A simple spring-mass system is a basic illustration of the momentum principle. The principle of conservation of momentum can be repeatedly applied to predict the system's future motion.

A Mathematical Model

The page Fundamentals of Iterative Prediction with Varying Force lays out the general methods of iterative prediction, but a brief recapitulation is provided here. he Momentum Principle provides a mathematical basis for the repeated calculations needed to predicts the system's future motion. The most useful form of this equation for predicting future motion is referred to as the momentum update form, and can be derived by rearranging the Momentum Principle as shown below:

[math]\displaystyle{ \Delta p = \vec{F}_{net}\Delta t }[/math]

[math]\displaystyle{ \vec{p}_{f} - \vec{p}_{i} = \vec{F}_{net}\Delta t }[/math]

[math]\displaystyle{ \vec{p}_{f} = \vec{p}_{i} + \vec{F}_{net}\Delta t }[/math]

Kinematics, expressed in a similarly iterative manner, allows for the determination of the next iteration's position and velocity

[math]\displaystyle{ \vec{v}_{f} = \frac{\vec{p}_f}{m} }[/math]

[math]\displaystyle{ \vec{r}_{f} = \vec{r}_{i} + \vec{v}_{avg}\Delta t }[/math]

Damping

We know from our observations of say a pendulum swinging or a spring bobbing that it's periodic motion eventually dies out. This is because dissipative forces prevalent such as air resistance, friction, fluid drag, etc. reduce the net energy of the system by dissipating it into the surroundings. A formal derivation of the equations of motion for a damped system will not be considered here, but it is very straightforward to add damping to our computational model. Whenever we calculate the net force on the mass during the iterative process, all we have to do now is add a dissipative force. For air resistance, the standard formula is

[math]\displaystyle{ \vec{F} = -0.5CAρv^2\hat{v} }[/math]

More frequently though, when we talk about the damped harmonic oscillator, we will discuss this force:

[math]\displaystyle{ \vec{F} = -b\vec{v} }[/math]

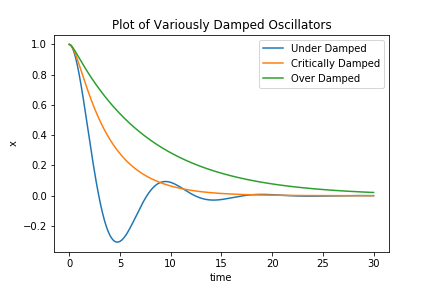
where b is the damping constant. The important difference between the two is that in the latter the force has a linear relationship to [math]\displaystyle{ \vec{v} }[/math]. There are three types of damping, depending on the coefficient. If the coefficient is small relative to the mass and spring constant, then the oscillator will be underdamped, and still have some oscillatory behavior. If it is large relative to the mass and spring constant, the oscillator will be overdamped, meaning that there will be no oscillations, but the system will take longer to arrive at an equilibrium because it has been slowed down by the dissipation. The fastest time of decay is when the system is critically damped, which occurs when [math]\displaystyle{ b^2 = 4mk }[/math]. The figure below illustrates these three possibilities, and is generated using the numpy based code from the Computational Methods section below.

A Computational Model

By definition, iterative prediction requires repeated calculations. This is extremely tedious to do by hand, so it is greatly preferable to perform them with a computer. Two programs are presented which perform these calculations.

An implementation of iterative motion for a spring system which feels gravitational force is provided in VPython here. The operative portion of the code is copied in the collapsible below (note, if one wishes to use this code, it will be necessary to include the proper import statements, which may be found at the link).

VPython Code

   ## constants and data
   g = 9.8
   mball = .5   ## mass of ball
   L0 = 0.3    ## relaxed length of spring
   ks = 50   ## spring constant (in N/m)
   deltat = .001  ## time step
   fscale = .07  ## scale factor for force arrow
   pscale = .4  ## scale factor for position arrow
   t = 0       ## initial time = 0 seconds
   ##########
   ## objects
   ceiling = box(pos=vec(0,0,0), size=vec(0.2,0.01,0.2)) ## origin is at ceiling
   ball = sphere(pos=vec(-.2637,-.1047,-.0429), radius=0.025, color=color.orange) ## note: spring initially compressed
   spring = helix(pos=ceiling.pos, color=color.cyan, thickness=.003, coils=40, radius=0.015)  ## create spring
   spring.axis = ball.pos - ceiling.pos  
   trail = curve(color=ball.color)  ## create trail of ball's position
   fnetarrow = arrow(pos = ball.pos, color = color.blue)  ## create arrow showing vector net force on ball
   parrow = arrow(pos = ball.pos, color = color.green)  ##create arrow showing vecotr momentum of ball
   ##########
   ## initial values
   ball.p = mball*vector  ## calculate initial momentum of ball
   #########
   ## improve the display
   scene.autoscale = 0             ## don't let camera zoom in and out as ball moves
   scene.center = vector(0,-L0,0)   ## move camera down to improve display visibility
   ##########
   ## calculation loop
   while t < 9.02:    ## sets end time for loop
       rate(300)
   ## calculate force on ball by spring
        l = ball.pos - ceiling.pos
        s = l.mag - L0
        lhat = l/l.mag
        fspring = ks * s * -lhat
   ## calculate net force on ball
        fnet = fspring + mball*vector(0, -g, 0)
        fnetarrow.pos = ball.pos
        fnetarrow.axis = fnet * fscale
   ## apply momentum principle
        ball.p = ball.p + fnet*deltat
        parrow.pos = ball.pos
        parrow.axis = ball.p * pscale
   ## update position
        ball.pos = ball.pos + (ball.p/mball)*deltat
   ## update axis of spring
        spring.axis = ball.pos - ceiling.pos
        trail.append(pos=ball.pos)
   ## update time   
        t = t + deltat
   ############
   ## Produce results
   print(ball.pos)
   print(ball.p/mball)

A second implementation using Numpy may be found here.

Examples

Simple Example

vertical spring-mass system

The simplest example of a spring mass system is one that moves in only one-direction.

Consider a massless spring of length 1.0 m with spring constant 40 N/m. If a 10 kg mass is released from rest while the spring is stretched downward to a length of 1.5 m, what is it's position after 0.2 seconds? The mass oscillates vertically, as shown to the right.

Step 1: Set Parameters Before we begin, we must set some parameters that allow the problem to be solved. Since all movement is in the vertical direction, no vector calculation is needed. However, careful attention must be paid to the direction associated with the object's movement and the forces acting on it. For ease in calculations, assume the origin is the point of attachment of the spring to the ceiling above. AS is customary, the positive y-direction will be up, and the negative-y, down. Additionally, the time step used for each iteration must be small enough that we can assume a constant velocity over the interval, but not so large that solving the problem becomes incredibly time-consuming. An appropriately small time step here is approximately 0.1 seconds.

Step 2: Calculate Initial Values Begin by calculating the object's initial momentum and the sum of the forces acting on it. The initial momentum is simply the product of the initial velocity, which is 0 m/s, as the object is released from rest. The forces acting on the mass are the gravitational force exerted by the Earth and the tension exerted by the spring. The net force can be calculated by summing these two forces.

[math]\displaystyle{ {\vec{p}_{i}} = {{m}\cdot\vec{v}_{i}} }[/math]

[math]\displaystyle{ {\vec{p}_{i}} = {{10kg}\cdot{0m/s}} = {0 Ns} }[/math]

[math]\displaystyle{ {\vec{F}_{grav}} = {mg} }[/math]

[math]\displaystyle{ {\vec{F}_{grav}} = {10kg}\cdot{-9.8 m/s/s} = {-9.8 N} }[/math]

[math]\displaystyle{ {\vec{F}_{spring}} = {-kx} }[/math]

[math]\displaystyle{ {\vec{F}_{spring}} = {-40N/m}\cdot{1.0m-1.5m} = {20 N} }[/math]

[math]\displaystyle{ {\vec{F}_{net}} = {\vec{F}_{grav} +{\vec{F}_{spring}}} }[/math]

[math]\displaystyle{ {\vec{F}_{net}} = {-9.8N} +{20 N} = {10.2} }[/math]

Step 3: Update Momentum (Iteration 1)

Using the momentum update formula, calculate the momentum of the mass at the end of the given time step.

[math]\displaystyle{ {\vec{p}_{f} = \vec{p}_{i} + \vec{F}_{net}{Δt}} }[/math]

[math]\displaystyle{ {\vec{p}_{f} = {0Ns} + {10.2N}\cdot{0.1s} = {1.02Ns}} }[/math]

Step 4: Update Velocity (Iteration 1)

[math]\displaystyle{ {\vec{v}_{f} = \vec{v}_{i} + \frac{\vec{F}_{net}}{m}}{Δt} }[/math]

[math]\displaystyle{ {\vec{v}_{f} = {0m/s} + \frac{1.02N}{1 kg}}{0.1s} = {0.102m/s} }[/math]

Step 5: Update Position (Iteration 1)

Using the position update formula, calculate the position of the mass at the end of the given time step. The average velocity used below is the velocity of the mass at the end of the time step. As with all simplifying assumptions, this measurement is not exact. However, it allows for a close enough approximation that the results derived are still valid.

[math]\displaystyle{ {\vec{r}_{f}} = {\vec{r}_{i} + \vec{v}_{avg}{Δt}} }[/math]

[math]\displaystyle{ {\vec{r}_{f}} = {-1.5m} + {0.102m/s}{0.1s} = {-1.398m} }[/math]

Step 6: Update Time (Iteration 1)

[math]\displaystyle{ {\vec{t}_{f}} = {\vec{t}_{i}} + {Δt} }[/math]

[math]\displaystyle{ {\vec{t}_{f}} = {0s} + {0.1s} = {0.1s} }[/math]

Step 7: Repeat Calculations

Repeat the above calculations using the "Iteration Round 1 Final Values" (calculated above) as the "Iteration Round 2 Initial Values".

Step 8: Update Forces (Iteration 2)

The gravitational force on the mass remains constant, and does not need to be recalculated.

[math]\displaystyle{ {\vec{F}_{spring}} = {-kx} }[/math]

[math]\displaystyle{ {\vec{F}_{spring}} = {-40N/m}\cdot{1.0m-1.398m} = {15.92 N} }[/math]

[math]\displaystyle{ {\vec{F}_{net}} = {\vec{F}_{grav} +{\vec{F}_{spring}}} }[/math]

[math]\displaystyle{ {\vec{F}_{net}} = {-9.8N} +{15.92 N} = {6.12N} }[/math]

Step 9: Update Momentum (Iteration 2)

[math]\displaystyle{ {\vec{p}_{f} = \vec{p}_{i} + \vec{F}_{net}{Δt}} }[/math]

[math]\displaystyle{ {\vec{p}_{f} = {1.02Ns} + {6.12N}\cdot{0.1s} = {1.632Ns}} }[/math]

Step 10: Update Velocity (Iteration 2)

[math]\displaystyle{ {\vec{v}_{f} = \vec{v}_{i} + \frac{\vec{F}_{net}}{m}}{Δt} }[/math]

[math]\displaystyle{ {\vec{v}_{f} = {0m/s} + \frac{1.632N}{1 kg}}{0.1s} = {0.1632m/s} }[/math]

Step 11: Update Position (Iteration 2)

[math]\displaystyle{ {\vec{r}_{f}} = {\vec{r}_{i} + \vec{v}_{avg}{Δt}} }[/math]

[math]\displaystyle{ {\vec{r}_{f}} = {-1.398m} + {0.1632m/s}{0.1s} = {-1.2348m} }[/math]

Step 12: State Answer

After 0.2 seconds, the mass is at a position of 1.23 m below the ceiling.

A Note on Iterations: While calculations can be performed manually, as above, it is advisable for more advanced problems that VPython or a similar program be used for such repetitive calculations in order to save time and reduce the likelihood of mathematical errors.

Middling Example

A semi-challenging problem, such as the one below, will often require you to perform vector calculations. However, the same steps as the easy example above still apply. Pay careful attention to signs as you solve these types of problems.

The simplest example of a spring mass system is one that moves in only one-direction.

Consider a massless spring of relaxed length 0.5 m with spring constant 120 N/m attached to the ceiling. If a 1.4 kg mass is released with an initial velocity of <1.2, 0.8, -0.2> m/s at an initial position of <-0.3, 0.7, 0.2> m, what is the velocity of the block after 0.005 seconds? Consider the point of attachment on the spring to the ceiling to be the origin. Only one iteration is necessary.

Step 1: Calculate Initial Momentum The initial momentum is simply the product of the mass and velocity of the object.

[math]\displaystyle{ {\vec{p}_{i}} = {{m}\cdot\vec{v}_{i}} }[/math]

[math]\displaystyle{ {\vec{p}_{i}} = {{1.4kg}\cdot{\lt 1.2, 0.8, -0.2\gt m/s}} = {\lt 1.68, 1.12, -0.28\gt Ns} }[/math]

Step 2: Calculate Force of Gravity

[math]\displaystyle{ {\vec{F}_{grav}} = {m}{\lt 0, -g, 0\gt } }[/math]

[math]\displaystyle{ {\vec{F}_{grav}} = {1.4kg}\cdot{\lt 0, -9.8, 0\gt m/s/s} = {\lt 0, -13.72, 0\gt N} }[/math]

Step 3: Calculate Force of Spring

[math]\displaystyle{ {\vec{F}_{spring}} = {-k}{(\vec{L}_{mag}-\vec{L}_{0})} \cdot {\hat{L}} }[/math]

The magnitude of L is equal to the square root of the squares of it's individual components

[math]\displaystyle{ {\hat{L}} = {\sqrt{ {{L}_{x}}^{2} + {{L}_{y}}^{2} + {{L}_{z}}^{2} }} }[/math]

[math]\displaystyle{ {\hat{L}} = {\sqrt{ {-0.3}^{2} + {0.7}^{2} + {0.2}^{2} }} = {\sqrt{0.62}} }[/math]

The unit vector of L ([math]\displaystyle{ {\hat{L}} }[/math]) is equal to L divided by its magnitude

[math]\displaystyle{ {\lVert\vec{L}\rVert} = {\frac{\vec{L}}{{\lVert\vec{L}\rVert}}} }[/math]

[math]\displaystyle{ {\lVert\vec{L}\rVert} = {\frac{\lt -0.3, 0.7, 0.2\gt m }{\sqrt{0.62}}} }[/math]

Substituting these values into Hooke's Law, then gives the force exerted by the spring:

[math]\displaystyle{ {\vec{F}_{spring}} = {-k}{(\lVert\vec{L}\rVert-\vec{L}_{0})} \cdot {\hat{L}} }[/math]

[math]\displaystyle{ {\vec{F}_{spring}} = {-120 N/m}{(\sqrt{0.62} m - {0.5 m})} \cdot {\frac{\lt -0.3, 0.7, 0.2\gt m }{\sqrt{0.62}}} }[/math]

[math]\displaystyle{ {\vec{F}_{spring}} = {\lt 12.83316, -29.94405, -8.55544\gt N} }[/math]

Step 4: Caculate Net Force"

The net force can be calculated by summing these two forces.

[math]\displaystyle{ {\vec{F}_{net}} = {\vec{F}_{grav} +{\vec{F}_{spring}}} }[/math]

[math]\displaystyle{ {\vec{F}_{net}} = {\lt 0, -13.72, 0\gt N} +{\lt 12.83316, -29.94405, -8.55544\gt N} = {\lt 12.83316, -16.22405, -8.55544\gt N} }[/math]

Step 5: Update Momentum

Using the momentum update formula, calculate the momentum of the mass at the end of the given time step.

[math]\displaystyle{ {\vec{p}_{f} = \vec{p}_{i} + \vec{F}_{net}{&Delta;t}} }[/math]

[math]\displaystyle{ {\vec{p}_{f} = {\lt 1.68, 1.12, -0.28\gt Ns} + {\lt 12.83316, -16.22405, -8.55544\gt N}\cdot{0.005s} = { Ns}} }[/math]

[math]\displaystyle{ {\vec{p}_{f} = {\lt 1.7442, 1.0389 ,-0.3611\gt Ns}} }[/math]

Step 4: Calculate Velocity

[math]\displaystyle{ {\vec{v}_{f}} = \frac{\vec{p}_{f}}{m} }[/math]

[math]\displaystyle{ {\vec{v}_{f}} =\frac{\lt 1.7442, 1.0389 ,-0.3611\gt Ns}{1.4kg} = {\lt 1.2458, 0.7421, -0.2579\gt m/s} }[/math]

Step 5: State Answer

After 0.005 seconds, the mass is moving with velocity <1.25, 0.74, -0.26> m/s

Difficult Example

Very difficult iterative motion problems likely require several calculation loops to be performed. Thus, it is recommended that a computer program, such as VPython, is used to solve these. For general instructions on how to do this, please see above in this article, under the heading A Computational Model.

Connectedness

While you may not need to precisely calculate the motion of spring-mass systems on a daily basis, understanding their behavior has led to the invention of many useful items. Among these are mattresses, clocks, and the suspension on cars.

However, the concept of iterative prediction applies to far more than masses on springs, as the concepts of physics apply far beyond textbook problems. By thinking in small enough time increments, the behavior of any system can be understood.

For example, in chemical engineering, entire processes can be broken down into simpler pieces and analyzed. These processes could then be modeled in order to predict future behavior.

See also

Conservation of Momentum

Predicting Change in multiple dimensions

Impulse and Momentum

Linear Momentum

Momentum Principle

Analytical Prediction

Net Force

Young's Modulus

Tension

Fundamentals of Iterative Prediction with Varying Force

Simple Harmonic Motion

Length and Stiffness of an Interatomic Bond

External links

Interactive Spring-Mass Simulator

References