Tension: Difference between revisions

Revision as of 18:30, 25 June 2019

Edited by Laurence Leon Summer 2019

Main Idea

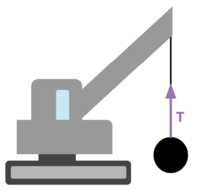
Tension is the force exerted by a rope (or anything that can be used to hang another object) on the object that is hanging from it. Usually, ropes and cables create a tension force. In general, anything that is flexible can pull an object and create a tension force. In consequence, the tension force can only be a pulling force. The rope will eventually go slack if someone tries to push with a rope, and it will act like an object. Later we will see that this concept will help with draing force diagrams with the force of tension always pulling the object.

Tension is considered a contact force which means that the force is exerted when objects are touching. Usually, the force of tension is the force that is transmitted through a rope. If someone is pulling on a block with a rope, the person exerting force on the rope which transmits that force to the block. In problems, the ropes and cables will usually be massless, which perfectly transfers the force.

Mathematical Model

There is no fundamental equation to calculate a tension force ([math]\displaystyle{ F_T }[/math]). Instead, one must usually deduce what the tension force must be based on the other forces acting on the object. To do this, Newton's Second and Third Laws will be very important.

We start by stating Newton's Second Law (the next force on a mass [math]\displaystyle{ M }[/math] is equal to the sum of the forces acting on the mass):

[math]\displaystyle{ F_{net} = \sum F = Ma }[/math]

The force of tension will end up being one of the forces in the sum. Furthermore, since the tension force usually acts between two objects (pulling each other in opposite directions), we usually get a system of equations (such as in a pulley system with two masses connected by a rope) that can be used to solve for the force of tension.

The examples will go in further detail.

Computational Model

In this code, a mass in the shape of a ball is hung from a 10 meter string, raised to an initial position, and then let go. With the loop, we follow the ball's pendulum-like motion.

from __future__ import division

from visual import *

from visual.graph import *

SCENE:

scene.title = "Mass on a String"

scene.background = color.black

CONSTANTS:

L = 10 #Length of string in meters

g = vector(0, -9.8, 0) #Acceleration due to gravity

mass = 5 #Mass of the ball in kilograms

OBJECTS:

ceiling = box(pos = vector(0, 0, 0), size = vector(20, 1, 1), color = color.red)

ball = sphere(pos = vector(10 * cos(-20 * (pi/180) ), 10 * sin(-20 * (pi/180)), 0), radius = 1, color = color.cyan)

string = curve(pos = [ceiling.pos, ball.pos], radius = .1, color = color.yellow)

trail = curve(pos = [ball.pos])

TIME:

time = 0 #Time in seconds

dtime = .001 #Time step for each iteration

ANGLE:

theta = - 20 * (pi / 180) #Angle to the vertical in radians #Left of the vertical is a negative angle #Right of the vertical is a positive angle #(-20) - (-160)

INITIAL CONDITIONS:

ball.p = vector(0,0,0) #Initial momentum of the block is 0

initpos = vector(-10 / 2**(1/2), -10 / 2**(1/2), 0)

CALCULATIONS:

Fgravity = mass * g #A vector

Ftension = vector(0,0,0)

LOOP:

while time < 10 and theta > -160 * (pi/180):

   rate(500)
   Ftension.y = -Fgravity.y
   magFtension = - Ftension.y / sin(theta) #Positive always
   Ftension.x = - magFtension * cos(theta) #Negative until theta < -90

   #Updates:
   ball.p.x += Ftension.x * dtime
   ball.pos.x += (ball.p.x * dtime) / mass
   if ball.pos.x >= 10:
       print(time)
       break
   ball.pos.y = -(100 - (ball.pos.x)**2)**(1/2)
   time += dtime
   theta = arctan(ball.pos.y/ball.pos.x)
   string.pos = [ceiling.pos, ball.pos]
   trail.append(ball.pos)

Examples

The three examples will be helpful in cementing an understanding in the concept of tension, and they will get harder as we go.

Simple

A [math]\displaystyle{ 2 \ \text{kg} }[/math] toy box is being dragged by a child. To do so, the child is pulling on a rope that is tied to the toy box. This rope makes an angle of [math]\displaystyle{ \theta = 60^\text{o} }[/math] with the horizontal. With the x-axis as the horizontal shown in the image, and the y-axis as the vertical shown in the image, the toy box gains an acceleration of:

[math]\displaystyle{ \mathbf{a} = \begin{bmatrix} a_x \\ a_y \end{bmatrix} = \begin{bmatrix} 3 \\ 0 \end{bmatrix} \frac{m}{s^2} }[/math]

a) Calculate the tension force [math]\displaystyle{ F_T }[/math] that is present in the child's rope:

First, we start by drawing a free body diagram for the toy box. The main forces acting on the box are the gravitational force, normal force, frictional force, and tension force.

INSERT FREE BODY DIAGRAM HERE

Now, we will right down the forces acting on the box:

[math]\displaystyle{ F_g = mg = 2 \times 9.81 = 19.62 \ \text{Newtons} }[/math]

[math]\displaystyle{ F_N = \ ? }[/math]

We know the normal force is not equal to the gravitational force because part of the tension accelerates the box upwards

[math]\displaystyle{ F_f = \mu_k F_N = \ ? }[/math]

We need to find the normal force to find this

[math]\displaystyle{ F_T = \ ? }[/math]

This is what we are looking to solve for

Next, we use Newton's Laws (mainly the second) to sum the forces along the x-axis and the y-axis and set them equal to their respective accelerations:

[math]\displaystyle{ F_{net_x} = \sum F_x = ma_{net_x} = F_T \ \text{cos}(\theta) - F_f = F_T \ \text{cos}(\theta) - \mu_k F_N = 2 \times 3 = 6 \ \text{Newtons} }[/math] (1)

[math]\displaystyle{ F_{net_y} = \sum F_y = ma_{net_y} = F_T \ \text{sin}(\theta) + F_N - F_g = F_T \ \text{sin}(\theta) + F_N - mg = 0 \ \text{Newtons} }[/math] (2)

We have two equations (1 and 2) and two unknowns ([math]\displaystyle{ F_N \ \text{and} \ F_T }[/math]). Therefore, we can solve for these two forces with our equations 1 and 2. We will add these two equations together:

[math]\displaystyle{ F_{net_x} + F_{net_y} = m(a_{net_x} + a_{net_y}) = F_T(cos(\theta) + sin(\theta)) + F_N(1 - \mu_k) - F_g = 6 }[/math]

Middling

A box with mass [math]\displaystyle{ m \ \text{kg} }[/math] hangs in a static state from two ropes. One rope is attached to the ceiling with an angle [math]\displaystyle{ \theta = 30^\text{o} }[/math] to the horizontal. The other rope, which pulls the box to the left, is along the horizontal (to the left of the box) and attached to a wall.

a) What is the tension in the rope attached to the wall ([math]\displaystyle{ F_{T_1} }[/math]) and the rope attached to the ceiling ([math]\displaystyle{ F_{T_2} }[/math])?

Difficult

A block of mass [math]\displaystyle{ M_1 }[/math] (block 1) is positioned on a ramp that is in the shape of an inclined plane. The angle between the horizontal and the inclined plane is [math]\displaystyle{ \theta = 45^\text{o} }[/math]. Block 1 has a string of negligible mass attached to it. This string loops over a pulley, and then connects to a block of mass [math]\displaystyle{ M_2 }[/math] (block 2), which is sitting on another inclined plane, whose angle to the horizontal is [math]\displaystyle{ \phi = 20^\text{o} }[/math]. Block 2 has another string of negligible mass attached to its opposite side. This string loops over another pulley, where it meets a block of mass [math]\displaystyle{ M_3 }[/math] (block 3). Block 3 is hanging off the edge of the table. Refer to the diagram for any confusion.

a) What are the direction and the magnitude of the acceleration of the system ([math]\displaystyle{ \mathbf{a_{system}} }[/math]) of blocks (blocks 1, 2, and 3):

Connectedness

Force of tension is used a lot in the real world, from small everyday things, such as yoyo's to large construction projections. In everyday life, force of tension can be seen when someone is trying to hang anything from somewhere else by a string. Tension can be very useful in construction as well because it can help support beams or other large objects. The rope has to be strong enough or else if there is too much force of tension, the rope could snap and drop whatever it is suppose to hold up.

One typical application of the force of tension is in elevators. If you look at a clear elevator, you can see all the ropes that hope the elevator up. The whole elevator system is acting as a pulley and pulling a rope up and letting it go down. The force of tension must be very meticulously calculated so that the rope is strong enough for a lot of people in the elevator. You can notice that most elevators will show what the maximum weight is, and that is calculated by seeing how much force of tension the ropes connected to the elevator can take and converting that to a maximum weight that it can hold. If there is too much weight in the elevator, it may break and the elevator will fall down the shaft.

History

Tension forces have been in use for centuries. Any system, for example a wooden pulley system one may have seen in a 1600's theatre, with a taut wire, cable, string, chain, etcetera uses the force of tension. Its wide use is no accident. Being able to attach a strong tension carrying material (like a chain)l to a heavy object, makes the lifting and moving of the object much easier. For example, no skyscraper is built without the use of large cranes. At the heart of a crane, a strong cable is looped around the heavy object, and then the crane can lift, rotate, and move an object that would be nearly impossible for us alone. In this way, most skyscrapers are built. It is speculated that the ancient Egyptians used a combination of inclined planes and strong ropes to build the pyramids.

We can see that the tension force has always been a very important part of construction, giving it a long history.

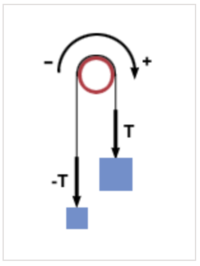
Tension is the force exerted by a rope (or anything that can be used to hang another object) on the object that is hanging from it. Usually, it is ropes and cables that have the tension force. In general, anything that is flexible can pull an object and have tension force. In consequence, the tension force can only be a pulling force. The rope will eventually go slack if someone tries to push with a rope, and it will act like just an object. Later we will see that this concept will help with draing force diagrams with the force of tension always pulling the object.

Tension is considered a contact force which means that the force is exerted when objects are touching. Usually, the force of tension is the force that is transmitted through a rope. If someone is pulling on a block with a rope, the person exerting force on the rope which transmits that force to the block. In problems, the ropes and cables will usually be massless, which perfectly transfers the force.

Mathematical Modeling

When calculating for tension force, tension force should be treated as one of the forces that is in the problem. The most important formula that will be used in this will be:

Fnet = Mass x Acceleration

This is based on Newton's Second Law, which applies because there will be multiple forces acting on the object so the forces must be added together. Because of this, we will also have to add all the forces together to find Fnet:

Fnet = F1 + F2 + ... + Fn for n number of forces.

A lot of times for simple force of tension problems, the acceleration may be 0, which causes our Fnet to be 0 (because Fnet = Mass x Acceleration). Acknowledging this will make calculating forces easier. This case will have to do with Newton's Third Law which sates that every force has an equal and opposite force; therefore, Fnet will be 0.

When acceleration is not 0, we will have to solve for Fnet and then for Ft (force of tension).

How To Calculate Tension Force

Because most situations of tension are different, there is no set way of calculating the force of tension. There are two situations in which we need to consider: zero acceleration and nonzero acceleration. Both will need the same steps, but zero acceleration will be easier to understand at first.

Tension Force with Zero Acceleration

1) Draw a free body diagram

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

The force of tension is shown by "T". There seems to be two forces of tension but they are actually the same magnitude because they come from the same string.

Whenever there is a question that has anything to do with force, the best thing to do first is to draw a free body diagram. This will help visualize the situation so you can see exactly where the forces will go. Common mistakes for force questions is that the direction of forces are wrong, so the student's solution turns out to be wrong. When drawing a free body diagram, make sure that the forces are all drawn in the right direction. Common forces to keep in mind when doing force of tension questions are:

Ft = Force of Tension
Fg = Force of Gravity
Ff = Force of Friction
Fn = Normal Force

2) Write equations that solve for Fnet

Because Fnet is 0 in this case because acceleration is 0, all the forces should add up to be 0. Make sure that the forces that are going in negative directions are negative. What could make this process easier is if you treat every force as the magnitude of the force and then add the magnitudes of the positive forces and subtract the magnitudes of the negative forces. That way, the negative signs will not get confused. Generally the equation would look like:

Fnet = 0 = Ft + F1 + F2 + ... + Fn (and then any other applied forces if there are any)

In this equation, the forces are not treated as magnitudes because the directions are not known. It is best to keep in note that the force of friction is usually going against velocity, and the force of gravity is usually pointing down in the y direction.

3) Solve for Ft

Once you have the equation done, it is possible to plug in forces to get to the solution for force of tension. If the problem does not give direct forces, here are some calculations of the forces:

Fg = mg
Ff = μFn
Fn is perpendicular to the surface of the object

Tension Force with Nonzero Acceleration

The way to solve this is very similar to the way tension force is solved with zero acceleration.

1) Draw a free body diagram

You should always draw a free body diagram to get started with visualizing the problem. Again, common forces to keep in mind when doing force of tension questions are:

Ft = Force of Tension
Fg = Force of Gravity
Ff = Force of Friction
Fn = Normal Force

2) Write equations that solve for Fnet

In a case where there is acceleration, the problem is basically stating that all the forces act together on an object to make it accelerate at that acceleration. Because Fnet = mass x acceleration, solving for the magnitude of Fnet is very easy:

Fnet = mass x acceleration

Then you would do the same thing for zero acceleration and set Fnet equal to all the forces added together. It should look something like this:

Fnet = mass x acceleration = Ft + F1 + F2 + ... + Fn

You will notice that this actually looks a lot like the equation before with zero acceleration. Actually, it is pretty much the same. Fnet is really just a variable for the total amount of force on the object and in each case it is like that. For zero acceleration, Fnet = 0, so we set the equation equal to zero. For a nonzero acceleration, we actually have to solve for Fnet before we move on.

3) Solve for Ft

Once you have the equation done, it is possible to plug in forces to get to the solution for force of tension.

Example Problems

Example 1: Angled rope pulling on a box

A 2.0kg box of toy box is being pulled across a table by a rope at an angle θ=60º as seen below (ignore friction). The tension in the rope causes the box to slide across the table to the right with an acceleration of 3.0 m/s^2. What is the tension on the rope?

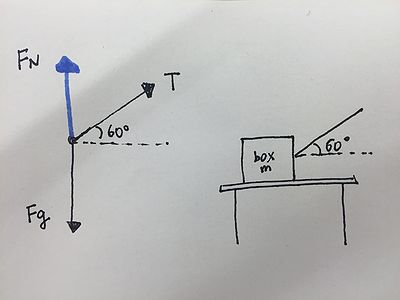
First always draw a free body diagram to visualize the situation better.

Fg: negative y direction

In most cases, the force of gravity is always present, and in this case, the force of gravity (Fg) is pointing in the negative y direction because gravity pulls objects down.

Fn: positive y direction

Because there is also a surface keeping the box standing up, there is a normal force (Fn) pushing the box up; therefore the direction of Fn is going in the positive y direction.

T: 60 degrees from x axis

In the image, the rope is pulling the block 60 degrees from the x axis; therefore the force of tension (T) is pointing that way.

Because the acceleration is nonzero in this situation, Fnet does not equal 0. So, which direction is net force going? The answer to this question is to always think about what direction acceleration is going. Fnet will be going in whatever direction acceleration is going. In this case, acceleration is going in the horizontal direction, so Fnet is pointing to the positive x direction. This can be confusing sometimes because it seems like Ft should be making the box go up as well, but the box does not move up; therefore Fnet is going in the positive x direction. So:

Fnet = mass x acceleration = 2 x 3 = 6N

It also can be noticed that Ft has two components: the y direction and the x direction. It would also help to differentiate between these two to see how T affects Fnet. So we can break down T into two parts:

T-y = Tsin(60)
T-x = Tcos(60)

Now if we separate the forces into y direction and x direction, we can see:

Y direction: Fn, Fg, T-y
X direction: T-x

It can also be noted from before that Fnet is going in the positive x direction, and the only force in the x direction is T-x. This means that all the y direction forces all add up to 0, and we only need to focus on T-x, and set it equal to Fnet. We found before that Fnet = 6N, so:

Fnet = T-x = Tcos(60) = 6
T = 12N

So, we get that the force of tension is 12N. Here is a quick version of all the calculations together:

a= Fnet/m (use Newtons's second law in the horizontal direction)
Fnet = (2.0kg)(3.0m/s^2) = 6N
6N=Tcos(60) (plug in the horizontal acceleration, mass, and horizontal forces)
T=6N/cos(60)
T=12N

Example 2: Box hanging from two ropes

A 0.25 kg container hangs at rest from two strings secured to the ceiling and wall respectively. The diagonal rope under tension T1 is directed at an angle θ=30º from the horizontal direction as seen below.

What are the tensions (T1 and T2) in the two strings?

First draw a force diagram of all the forces acting on the container.

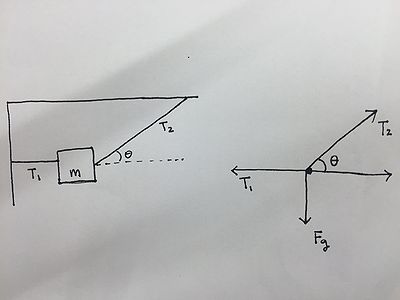
Now use Newton's second law. There are tensions directed both vertically and horizontally, so again it's a little unclear which direction to choose. However, since there is force of gravity (a vertical force), start with Newton's second law in the vertical direction.

a=ΣF/m (use Newton's second law for the vertical direction)
0=(T2*sin30º-Fg)/0.25kg
T2=Fg/(sin30º)
T2=mg/(sin30º)
T2=[(0.25kg)(9.8m/s²)]/(sin30º)
T2=4.9N

Now that we know T2 we can solve for the tension T1 using Newton's second law for the horizontal direction.

a=ΣF/m (use Newton's second law for the horizontal direction)
0=(T2*cos30º-T1)/0.25kg (plug in the horizontal acceleration, mass, and horizontal forces)
T1=T2*cos30º
T1=(4.9N)*cos30º
T1=4.2N

Connectedness

Force of tension is used a lot in the real world from small everyday things to large construction. In everyday life, force of tension can be seen when someone is trying to hang anything from somewhere else by a string. Tension can be very useful in construction as well because it can help support beams or other large objects. The rope has to be strong enough or else if there is too much force of tension, the rope could snap and drop whatever it is suppose to hold up.

One typical application of the force of tension is in elevators. If you look at a clear elevator, you can see all the ropes that hope the elevator up. The whole elevator system is acting as a pulley and pulling a rope up and letting it go down. The force of tension must be very meticulously calculated so that the rope is strong enough for a lot of people in the elevator. You can notice that most elevators will show what the maximum weight is, and that is calculated by seeing how much force of tension the ropes connected to the elevator can take and converting that to a maximum weight that it can hold. If there is too much weight in the elevator, it may break and the elevator box will fall.

References

Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. Hoboken, NJ: John Wiley & Sons, 2015. Print. https://www.khanacademy.org/science/physics/forces-newtons-laws/tension-tutorial/a/what-is-tension http://www.physicsclassroom.com/Class/newtlaws/U2L2b.cfm#tension http://hyperphysics.phy-astr.gsu.edu/hbase/mlif.html http://hyperphysics.phy-astr.gsu.edu/hbase/elev.html http://www.sparknotes.com/physics/dynamics/newtonapplications/problems_2.html http://philschatz.com/physics-book/contents/m42075.html http://www.mrwaynesclass.com/freebodies/reading/pics/Tension_Explained_Diagram.png http://www.softschools.com/formulas/physics/tension_formula/70/ http://physics.stackexchange.com/questions/36175/understanding-tension http://www.brightstorm.com/science/physics/newtons-laws-of-motion/tension/

@@ Line 164: / Line 164: @@
 :::<math>F_{net_y} = \sum F_y = ma_{net_y} = F_T \ \text{sin}(\theta) + F_N - F_g = F_T \ \text{sin}(\theta) + F_N - mg = 0 \ \text{Newtons}</math> '''(2)'''
-::We have two equations (1 and 2) and two unknowns (<math>F_N \ \text{and} \ F_T</math>). Therefore, we can solve for these two forces with our equations 1 and 2:
+::We have two equations (1 and 2) and two unknowns (<math>F_N \ \text{and} \ F_T</math>). Therefore, we can solve for these two forces with our equations 1 and 2. We will add these two equations together:
+:::<math>F_{net_x} + F_{net_y} = m(a_{net_x} + a_{net_y}) = F_T(cos(\theta) + sin(\theta)) + F_N(1 - \mu_k) - F_g = 6</math>
 ===Middling===

Tension: Difference between revisions

Revision as of 18:30, 25 June 2019

Contents

Main Idea

Mathematical Model

Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further Reading

External Links

References

Main Idea

What is Tension?

Mathematical Modeling

How To Calculate Tension Force

Tension Force with Zero Acceleration

Tension Force with Nonzero Acceleration

Example Problems

Example 1: Angled rope pulling on a box

Example 2: Box hanging from two ropes

Connectedness

See also

External links

References

Navigation menu