Field of a Charged Rod: Difference between revisions

Revision as of 09:20, 3 August 2019

This entire page and all its contents were created by Lukas Yoder, PHYS 2212 Class of Fall 2018

(After finishing this, I found an article called Charged Rod written by the people of yesteryear. I didn't see that and created this new one instead. The 2 should be merged in the future.)

The Main Idea

Previously, we've learned about the electric field of a point particle. Often, when analyzing physical systems, it is the case that we're unable to analyze each individual particle that composes an object and need to therefore generalize collections of particles into shapes (in this case, a rod) whereby the mathematics corresponding to electric field calculations can be simplified. This can essentially be done by adding up the contributions to the electric field made by parts of an object, approximating each part of an object as a point charge.

A Mathematical Model

The System in Question

As discussed in the previous section, we're considering a system abstracted from the particle model we're familiar with, therefore we will make the generalization that our rod of length L has a total charge of quantity Q. For this generalization, we will need to assume that the rod is so thin that we can ignore its thickness.

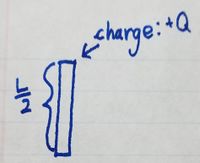
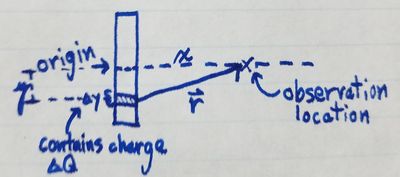
Since the electric field produced by a charge at any given location is proportional to the distance from the charge to that location, we will need to relate the observation location to the source of the charge, which we will consider the origin of the rod. To do that, we will need to divide the rod into pieces of length [math]\displaystyle{ \Delta y }[/math] each containing a charge [math]\displaystyle{ \Delta Q }[/math]. In the image below, you can see what this looks like and the relation that can be found between the observation location and the source, forming the distance vector [math]\displaystyle{ \vec{r} }[/math].

By the pythagorean theorem, we can find the vector [math]\displaystyle{ \vec{r} }[/math] as follows:

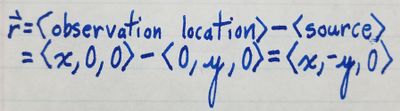
And to find the unit vector in the direction of [math]\displaystyle{ \vec{r} }[/math], [math]\displaystyle{ \hat{r} }[/math], we do as follows:

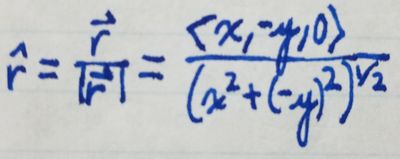
Finding the Contribution of Each Piece to the Electric Field

Now that we've set up a model for the system, with the rod broken down into pieces, we can find the contribution of each piece to the electric field of the system. We will start from the electric field equation you learned for a point particle but plug in the parameters for the rod system into the equation.

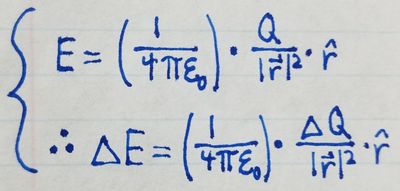
By mathematically simplifying, we then get the following equation:

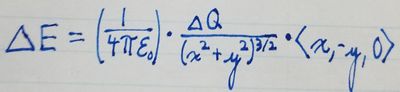
Finding the Net Contribution of all Pieces

In the previous section, we found out the contribution to the electric field at a given location of only one of the pieces constituting the rod. In order to figure out the net field at any particular location, we need to add up the electric fields produced by individual pieces along the length of the rod.

We will switch from vector notation for the electric field to the scalar notation for the x- and y-components. (From the vector in the equation above, we can see that the z-component of the electric field at any point is always 0.) The x-component of the electric field is the sum of the x-components of every [math]\displaystyle{ \Delta{y} }[/math] along the rod, and the y-component of the electric field is the sum of the y-components of every [math]\displaystyle{ \Delta{y} }[/math] along the rod. We can show this mathematically:

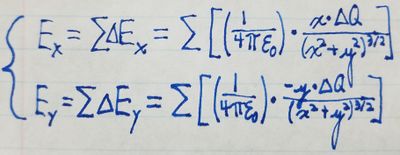
To make use of this relation, because we don't know [math]\displaystyle{ \Delta{Q} }[/math], we need to relate it to parameters that we already know about the rod system we're analyzing. We can express [math]\displaystyle{ \Delta{Q} }[/math] as the charge density of the rod (which is Q/L) times the [math]\displaystyle{ \Delta{y} }[/math] we've chosen for the system. Thus,

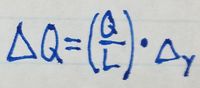
By plugging the above equation into our equations for the x- and y-components of the electric field at a point, we can find the electric field at any point in the system. This technique is called numerical integration and is typically done by computers because the computational complexity is dependant upon the size of [math]\displaystyle{ \Delta{y} }[/math] with respect to L.

Simplifying

Using calculus, we can simplify a lot of the math required to compute the electric field at any given point. Notationally, all we're doing is switching from the discretely-sized [math]\displaystyle{ \Delta{y} }[/math] to [math]\displaystyle{ dy }[/math] and from the sigma notation to an integral starting from -L/2 (the lower end of the rod) and ending at L/2 (the upper end of the rod) as follows:

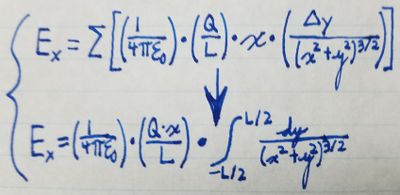
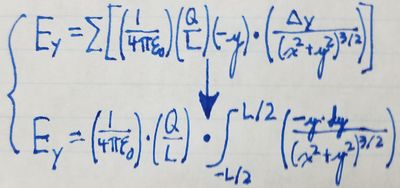
By evaluating the integral, we can determine that the x-component of the electric field at any point is:

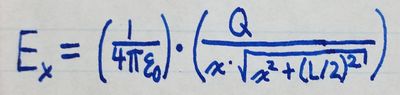
Without evaluating the integral for the y-component of the electric field, we can use symmetry to determine that the y-component of the electric field at any given point is 0. Let's consider the contributions to the electric field from the top and bottom halves of the rod at any observation point.

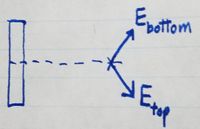
Since the y-components of [math]\displaystyle{ E_{top} }[/math] and [math]\displaystyle{ E_{bottom} }[/math] are of equal magnitude and opposite direction, they cancel each other out, and therefore the y-component of teh electric field at any given point due to the rod is 0.

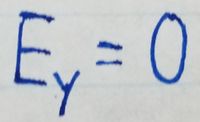
Finally, because the rod is round and can be rotated, as a convenience, we'll use d (distance from the rod) as opposed to x (distance along the x-direction) to refer to the electric field.

Thus we can simplify electric field calculations for a rod into a form that we can readily use:

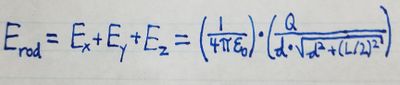
Further Simplification

By noting the contributions of each variable to the equation for the electric field, we can make approximations to simplify our math by simply declaring one variable as insignificant.

For example, if we have a system in which the length of a rod is much greater than the magnitude of the distance from the rod (denoted L>>d), we can neglect some of the instances in which d is taken into account as follows:

A Computational Model

(Finding the Electric Field from a Rod with Code)

Here is some code that you can run which shows the electric field vector at a given distance from the rod along its length. The rod is shown as a series of green balls to help emphasize that when using the numerical integrations mentioned on this page, you are measuring the field produced by discrete parts of the rod being analyzed.

Notice the edge-effects of the electric field of the rod. For reasons discussed above, if we used the long rod approximation (L>>d), these effects would be negligible.

Click Here to Run the Code

Examples

Although this is not a very difficult topic, some reasonably difficult conceptual questions can be asked about it.

Simple

Middling

Difficult

Connectedness

Electric fields are very important to electrical engineering because they can be used to convey signals. In fact, there is an entire sub-field of electrical engineering called digital signal processing that focuses on modulating different characteristics of radio frequency (RF) signals that are produced by electric fields.

History

The history of the electric field can be found in a previous section on electric fields. The equation for the electric field of a charged rod was not a discovery, but simply a mathematical simplification that someone made to model a rod. As such, nobody knows who first made the mathematical simplification, where they made it, or when, though it was certainly made after electric fields were discovered.

(For the above reference, I chose to follow the textbook's method in not defining the charge distribution and assuming it was constant, though this was helpful in figuring out a better way to introduce it.)

Chabay and Sherwood: Matter and Interactions, Fourth Edition, Chapter 15

All figures created by author