Temperature: Difference between revisions
| Line 35: | Line 35: | ||
:::<math>Q = mCT</math> | :::<math>Q = mCT</math> | ||
====Thermal Expansion==== | |||
A change in the Temperature of a body through Heat transfer can change the shape, area, and volume of the body. When a substance is heated, the kinetic energy of its molecules increases. Then, the molecules begin moving more and more, and the average separation between molecules become larger, and thus the volume of the body changes. The degree of expansion divided by the change in Temperature is called the material's Coefficient of Thermal Expansion and generally varies with Temperature, the object, and state of matter of the object. | |||
{| border="1" style="text-align:center; margin-left:auto; margin-right:auto" | |||
|+ | |||
! Material !! Fractional expansion per <math>°C</math> <math>(10^{-6})</math> !! Fractional expansion per <math>°F (10^{-6})</math> | |||
|- | |||
! Glass (Ordinary) | |||
| 9 | |||
| 5 | |||
|- | |||
! Glass (Pyrex) | |||
| 4 | |||
| 2.2 | |||
|- | |||
! Quartz (Fused) | |||
| .59 | |||
| .33 | |||
|- | |||
! Aluminum | |||
| 24 | |||
| 13 | |||
|- | |||
! Brass | |||
| 19 | |||
| 11 | |||
|- | |||
! Copper | |||
| 17 | |||
| 9.4 | |||
|- | |||
! Iron | |||
| 12 | |||
| 6.7 | |||
|- | |||
! Steel | |||
| 13 | |||
| 7.2 | |||
|- | |||
! Platinum | |||
| 9 | |||
| 5 | |||
|- | |||
! Tungsten | |||
| 4.3 | |||
| 2.4 | |||
|- | |||
! Gold | |||
| 14 | |||
| 7.8 | |||
|- | |||
! Silver | |||
| 18 | |||
| 10 | |||
|- | |||
|} | |||
===Computational Model=== | ===Computational Model=== | ||
Revision as of 11:50, 6 August 2019
Main Idea
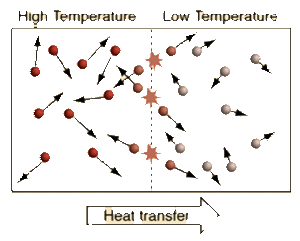
Temperature is the measure of the Average Kinetic Energy of the particles in a system. The difference between Temperature, Thermal Energy, and Heat is:
Thermal Energy is the sum of all the kinetic energies of the particles in a system
Heat is the transfer of Thermal Energy
Applying Heat to a system usually causes its Temperature to rise; the loss of Heat by a system typically corresponds to decrease in Temperature. The Zeroth Law of Thermodynamics states:
If system A is in Thermodynamic Equilibrium with system B, and if system B is in Thermodynamic Equilibrium with system C, then system A is also in Thermodynamic Equilibrium with system C
Thermodynamic Equilibrium is defined as:
When a system has no Heat exchange with itself
Thus, a system's Temperature is the same throughout when it is in Thermodynamic Equilibrium.
We see from the definition of Thermodynamic Equilibrium and The Zeroth Law of Thermodynamics that a Temperature difference is needed for Heat to flow from a warmer Temperature system to a cooler Temperature system. When systems with different Temperatures are in contact, the molecules in the system with higher average kinetic energy collide with the molecules of the system with lower average kinetic energy; kinetic energy is passed from the molecules with more kinetic energy to those with less kinetic energy. This molecular level of kinetic energy transfer will happen until the average kinetic energy of the particles in each system reaches the weighted average of the two systems. This idea can be applied to a multi-system interaction as well.
Mathematical Model
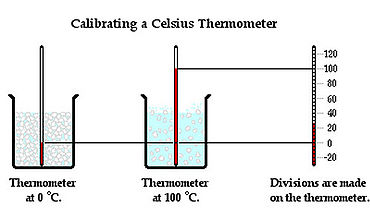
A thermometer is a device used to measure the Temperature of a system. It is placed in contact with an object and allowed to reach Thermal Equilibrium with the object, and thus the same Temperature. The operation of a thermometer is based on some property, such as volume, that varies with Temperature. For example, mercury in a mercury thermometer expands to a degree depending on a temperature of the object and the level of the mercury inside the glass tube rises or descends due to this.
Temperature can be measured in numbers by three Temperature scales: Celsius, Fahrenheit, and Kelvin. The Celsius scale sets the freezing point of the water at 0 degrees and the boiling point of water at 100 degrees. The Fahrenheit scale sets the freezing point of water at 32 degrees and the boiling point of the water at 212 degrees. The Kelvin scale is designed to go to 0 at absolute zero, the minimum possible temperature in the Universe.
The three Temperature scales are related by the following:
- [math]\displaystyle{ °K = 273.15 + °C }[/math]
- [math]\displaystyle{ °C = \left(\frac{5}{9}\right)(°F - 32) \quad \And \quad °C = °K - 273.15 }[/math]
- [math]\displaystyle{ °F = \left(\frac{9}{5}\right)(°C + 32) }[/math]
The relationship between Heat transfer and Temperature can be modeled with this equation:
- [math]\displaystyle{ Q = mCT }[/math]
Thermal Expansion
A change in the Temperature of a body through Heat transfer can change the shape, area, and volume of the body. When a substance is heated, the kinetic energy of its molecules increases. Then, the molecules begin moving more and more, and the average separation between molecules become larger, and thus the volume of the body changes. The degree of expansion divided by the change in Temperature is called the material's Coefficient of Thermal Expansion and generally varies with Temperature, the object, and state of matter of the object.
| Material | Fractional expansion per [math]\displaystyle{ °C }[/math] [math]\displaystyle{ (10^{-6}) }[/math] | Fractional expansion per [math]\displaystyle{ °F (10^{-6}) }[/math] |
|---|---|---|
| Glass (Ordinary) | 9 | 5 |
| Glass (Pyrex) | 4 | 2.2 |
| Quartz (Fused) | .59 | .33 |
| Aluminum | 24 | 13 |
| Brass | 19 | 11 |
| Copper | 17 | 9.4 |
| Iron | 12 | 6.7 |
| Steel | 13 | 7.2 |
| Platinum | 9 | 5 |
| Tungsten | 4.3 | 2.4 |
| Gold | 14 | 7.8 |
| Silver | 18 | 10 |
Computational Model
- Insert Computational Model here
Examples
Simple
Complete the following Temperature table:
| Fahrenheit [math]\displaystyle{ (°F) }[/math] | Celsius [math]\displaystyle{ (°C) }[/math] | Kelvin [math]\displaystyle{ (°K) }[/math] |
|---|---|---|
| [math]\displaystyle{ 142 }[/math] | ? | ? |
| ? | ? | [math]\displaystyle{ 31 }[/math] |
| ? | [math]\displaystyle{ 350 }[/math] | ? |
- Row 1:
- [math]\displaystyle{ 142°F: °C = \left(\frac{5}{9}\right)(142 - 32) = \left(\frac{5}{9}\right)(110) \approx 61.11°C }[/math]
- [math]\displaystyle{ 61.11°C: °K = 273.15 + °C \approx 273.15 + 61.11 = 334.26°K }[/math]
- Row 2:
- [math]\displaystyle{ 31°K: °C = °K - 273.15 = 31 - 273.15 = -242.15°C }[/math]
- [math]\displaystyle{ -242.15°C: °F = \left(\frac{9}{5}\right)(°C + 32) = \left(\frac{9}{5}\right)(-241.15 + 32) = \left(\frac{9}{5}\right)(-210.15) = -116.75°F }[/math]
- Row 3:
- [math]\displaystyle{ 350°C: °F = \left(\frac{9}{5}\right)(°C + 32) = \left(\frac{9}{5}\right)(350 + 32) = \left(\frac{9}{5}\right)(382) = 687.2°F }[/math]
- [math]\displaystyle{ 350°C: °K = 273.15 + °C = 273.15 + 350 = 623.15°K }[/math]
- Now, we can fill in the table:
| Fahrenheit [math]\displaystyle{ (°F) }[/math] | Celsius [math]\displaystyle{ (°C) }[/math] | Kelvin [math]\displaystyle{ (°K) }[/math] |
|---|---|---|
| [math]\displaystyle{ 142 }[/math] | [math]\displaystyle{ 61.11 }[/math] | [math]\displaystyle{ 334.26 }[/math] |
| [math]\displaystyle{ -116.75 }[/math] | [math]\displaystyle{ -242.15 }[/math] | [math]\displaystyle{ 31 }[/math] |
| [math]\displaystyle{ 687.2 }[/math] | [math]\displaystyle{ 350 }[/math] | [math]\displaystyle{ 623.15 }[/math] |
Middling
On Thanksgiving morning, your mom cooked a turkey with a mass of [math]\displaystyle{ m = 12.55 \ kg }[/math]. It had a Temperature of [math]\displaystyle{ 85°C }[/math] coming out of the oven. By the time everyone is seated at the table and ready to eat the turkey, its Temperature is now [math]\displaystyle{ 43°C }[/math]. The specific heat for the turkey is [math]\displaystyle{ 5.16 \left(\frac{J}{g \cdot C}\right) }[/math].
- a) Determine the Heat lost by the turkey.
- We can use this equation to relate the Heat loss to the Temperature change:
- [math]\displaystyle{ \Delta Q = mC \Delta T }[/math]
- First, we will convert the mass of the turkey to grams:
- [math]\displaystyle{ m_{kg} = 12.55 \ kg \quad \And \quad 1 \ kg = 1,000 \ g \quad \therefore \quad m_{g} = 12.55 \ (kg) \times \frac{1,000}{1} \ \left(\frac{g}{kg}\right) = 12,550 \ g }[/math]
- Now, we can calculate the change in Thermal Energy of the turkey:
- [math]\displaystyle{ \Delta Q = m_{g} C \Delta T_{turkey} = 12,550 \times 5.16 \times (43 - 85) = -2,719,836 \ J }[/math]
Difficult
You take a slice of the turkey. This slice has a mass of [math]\displaystyle{ m_{slice} = 1.12 \ kg }[/math]. The Temperature of it is [math]\displaystyle{ 85°F }[/math]. You also place some sauce on top of it. The sauce has a mass of [math]\displaystyle{ m_{sauce} = 0.044 \ kg }[/math], an initial temperature [math]\displaystyle{ T_{sauce_{0}} = 65°F }[/math] , and a specific heat of [math]\displaystyle{ C_{sauce} = 2.2 \ \left(\frac{J}{g \cdot C}\right) }[/math].
a) Assuming the slice of turkey and the sauce are an isolated system, what is the final Temperature reached in Thermodynamic Equilibrium?
- Within an isolated system, energy must be conserved. Also, the only kind of change in energy is through Heat; no Work is being done. The Thermal Energy of the slice of turkey will warm the sauce.
- Thus, we can use the Energy Principle to describe the scenario:
- [math]\displaystyle{ \Delta E_{system} = Q + W = 0\quad \And \quad W = 0 }[/math]
- [math]\displaystyle{ \Delta E_{system} = Q = 0 }[/math]
- This change in energy of the system is a change in Thermal Energy:
- [math]\displaystyle{ \Delta Q_{system} = Q = 0 \quad \And \quad \Delta Q = mC \Delta T }[/math]
- [math]\displaystyle{ \Delta Q_{system} = \Delta Q_{slice} + \Delta Q_{sauce} = 0 }[/math]
- [math]\displaystyle{ \Delta Q_{slice} + \Delta Q_{sauce} = m_{slice}C_{turkey} \Delta T_{slice} + m_{sauce}C_{sauce} \Delta T_{sauce} = 0 }[/math]
- [math]\displaystyle{ m_{slice}C_{turkey} \Delta T_{slice} + m_{sauce}C_{sauce} \Delta T_{sauce} = m_{slice}C_{turkey}(T_{f} - T_{slice_{0}}) + m_{sauce}C_{sauce}(T_{f} - T_{sauce_{0}}) = 0 }[/math]
- [math]\displaystyle{ (m_{slice}C_{turkey} + m_{sauce}C_{sauce}) T_{f} = m_{slice}C_{turkey}T_{slice_{0}} + m_{sauce}C_{sauce}T_{sauce_{0}} }[/math]
- [math]\displaystyle{ T_{f} = \frac{m_{slice}C_{turkey}T_{slice_{0}} + m_{sauce}C_{sauce}T_{sauce_{0}}}{m_{slice}C_{turkey} + m_{sauce}C_{sauce}} }[/math]
- Now, we need to convert the Fahrenheit Temperatures to Celsius and kilograms to grams:
- [math]\displaystyle{ T_{slice_{0}}(°C) = \left(\frac{5}{9}\right)(T_{slice_{0}}(°F) - 32) = \left(\frac{5}{9}\right)(85 - 32) = \left(\frac{5}{9}\right)(53) \approx 29.44°C }[/math]
- [math]\displaystyle{ T_{sauce_{0}}(°C) = \left(\frac{5}{9}\right)(T_{sauce_{0}}(°F - 32) = \left(\frac{5}{9}\right)(65 - 32) = \left(\frac{5}{9}\right)(33) \approx 18.33°C }[/math]
- [math]\displaystyle{ m_{slice}: 1.12 \ (kg) \times \frac{1,000}{1} \left(\frac{g}{kg}\right) = 1,120 \ g }[/math]
- [math]\displaystyle{ m_{sauce}: 0.044 \ (kg) \times \frac{1,000}{1} \left(\frac{g}{kg}\right) = 44 \ g }[/math]
- We can calculate the final Temperature of the system now:
- [math]\displaystyle{ T_{f} = \frac{(1,120 \times 5.16 \times 29.44) + (44 \times 2.2 \times 18.33)}{(1,120 \times 5.16) + (44 \times 2.2)} = \frac{(170,139.648) + (1,774.344)}{(5,779.2) + (96.8)} = \frac{171,913.992}{5,876} = 29.257°C }[/math]
Connectedness
History

Early explanations of Heat were thoroughly confused with explanations of combustion. J. J. Becher and George Ernst Stahl introduced the Phlogiston Theory of Combustion in the 17th century, and Phlogiston was thought to be the substance of Heat.
In late 18th century, Antoine Lavoisier argued that Phlogiston Theory is inconsistent, and introduced Caloric Theory. The suggested explanation was that when an object was heated, an invisible fluid called “caloric” was added to the object. Hot objects contained more caloric than cold objects. Caloric theory was popularly accepted until the mid 19th century.
Followed by introduction of Caloric Theory, Count Rumford found that boring a cannon repeatedly does not result in Heat producing ability, and therefore caloric is not lost. This proposed that caloric might not be a substance, though the experimental ambiguity in this experiment was widely considered controversial.
In the mid 19th century, Rudolf Clausius showed that Rumford's argument and Caloric Theory can be agreeable if the Caloric Theory included the principle of conservation of energy in place of its original principle of conservation of Heat. By doing so, the Caloric Theory was able to be evolved into modern Thermodynamics where Heat is described as the transfer of Thermal Energy, which is equivalent to the kinetic energy of the particles of a substance.
See also
Further reading
- http://hyperphysics.phy-astr.gsu.edu/hbase/tables/thexp.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/temper.html
- http://teachers.oregon.k12.wi.us/mahr/assignments/thermal_energyvs_temp.pdf
External links
- https://en.wikipedia.org/wiki/Thermal_equilibrium
- http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/thereq.html
- https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_II_-_Thermodynamics%2C_Electricity%2C_and_Magnetism_(OpenStax)/1%3A_Temperature_and_Heat/1.1%3A_Temperature_and_Thermal_Equilibrium
- https://en.wikipedia.org/wiki/Zeroth_law_of_thermodynamics