The Maxwell-Boltzmann Distribution

The Main Idea

In the context of the Kinetic Molecular Theory of Gases (KMToG), a gas has a large number of particles moving around with varying speeds, colliding with each other, causing changes in the speeds and directions of the particles. A good understanding of the properties of a gas requires the knowledge of the distribution of particles speeds. Named after James Clerk Maxwell and Ludwig Boltzmann, the Maxwell-Boltzmann Distribution describes particle speeds in an idealized gas, in which the particles rarely interact with each other except for the brief collisions where energy and momentum are affected. The distribution of a particular gas depends on certain parameters, such as the Temperature of the system and mass of the gas particles. Certain properties of real gases inhibit their ability to be modeled by the Maxwell-Boltzmann Distribution so this distribution is best suited for application to ideal gases and certain rarefied gases at normal Temperatures. Knowledge of particle speeds given by this distribution is important to scientists performing reactions, because for a reaction to take place, particles must collide with sufficient energy to induce a transition state. This usually pertains to faster particles, so if the Maxwell-Boltzmann Distribution tells us how many particles have energies or speeds above a certain threshold, this is considered valuable information.

A Mathematical Model

The Maxwell–Boltzmann distribution is the function:

[math]\displaystyle{ f(v) = \sqrt{\left(\frac{m}{2 \pi kT}\right)^3}\, 4\pi v^2 e^{- \frac{mv^2}{2kT}} }[/math], where

[math]\displaystyle{ m = }[/math] the mass of a particle

[math]\displaystyle{ k = }[/math] Boltzmann's constant

[math]\displaystyle{ T = }[/math] Thermodynamic Temperature

[math]\displaystyle{ v = }[/math] the speed of the particle

The probability that a molecule of a gas has a center-of-mass speed within the range [math]\displaystyle{ v }[/math] to [math]\displaystyle{ v+dv }[/math] is given by [math]\displaystyle{ f(v)dv }[/math].

As has been mentioned, the Maxwell-Boltzmann Distribution details the distribution of particle speeds in an ideal gas, and this distribution can be characterized in a few ways shown below:

- The average speed, [math]\displaystyle{ v_{avg} }[/math], is the sum of the speeds of all particles divided by the number of particles in the volume of gas:

[math]\displaystyle{ v_{avg} = \int_0^{\infty} v \, f(v) \, dv= \sqrt { \frac{8kT}{\pi m}}= \sqrt { \frac{8RT}{\pi M}} }[/math]

where R is the gas constant and M is the molar mass of the substance.

- The most probable speed, [math]\displaystyle{ v_p }[/math], is the speed associated with the highest point on the Maxwell-Boltzmann Distribution curve. Only a few particles will have this speed. To find this point on the distribution, we must calculate df/dv, set it equal to zero, and then solve for v. Then, we can ascertain:

[math]\displaystyle{ v_p = \sqrt { \frac{2kT}{m} } = \sqrt { \frac{2RT}{M} } }[/math]

-The root-mean-square speed, [math]\displaystyle{ v_{rms} }[/math], is the square root of the average speed-squared and is given by:

[math]\displaystyle{ v_{rms} = \left(\int_0^{\infty} v^2 \, f(v) \, dv \right)^{1/2}= \sqrt { \frac{3kT}{m}}= \sqrt { \frac{3RT}{M} } }[/math]

If a gas is in thermal equilibrium and follows the Maxwell-Boltzmann Distribution, the following relation always is discovered:

[math]\displaystyle{ v_p \lt v_{avg} \lt v_{rms} }[/math]

A Computational Model

Maxwell-Boltzmann Distributions are not only represented by functions, but they are also represented by graphs. These graphs can tell scientists a lot about the properties of a gas. They can detail gas particles' masses and speeds, and the graphs can also tell a scientist how the gas responds to variations in temperature.

To visualize how a Maxwell-Boltzmann Distribution plot looks like, the link below provides a demonstration to see how temperature of the system affects the particle speeds.

Maxwell-Boltzmann Temperature Effect Demo

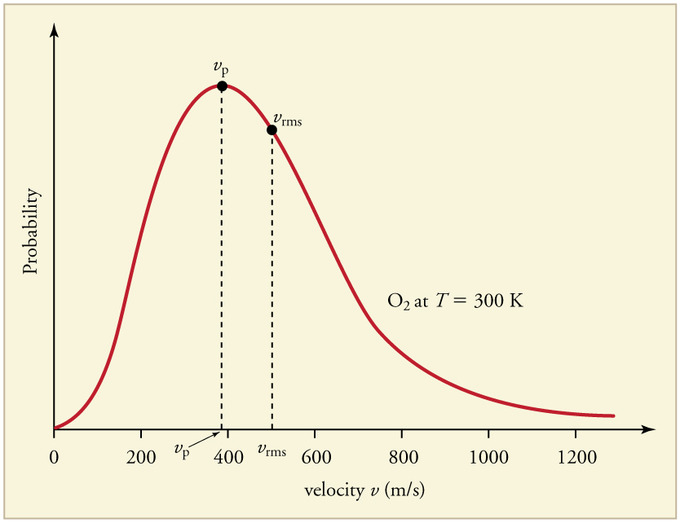
The graph below displays the Maxwell-Boltzmann Distribution of [math]\displaystyle{ O_2 }[/math] at 300 Kelvin. As one can see, the most probable speed, [math]\displaystyle{ v_p }[/math], is marked at the peak of the distribution curve. The root-mean-square speed, [math]\displaystyle{ v_{rms} }[/math], is also displayed on the curve.

Credit for this image is given to chemwiki.ucdavis.edu

Examples

Below are some examples of how the Maxwell-Boltzmann equation is used and how to interpret the distribution graphs.

Simple

Looking at the Maxwell-Boltzmann Distributions of several gases below, what can be said about the relationship between particle speed distributions and the mass of the particles?

Credit for this image is given to chemwiki.ucdavis.edu

It can be concluded that the heavier particles move slower on average and have a smaller range of particle speeds, whereas lighter particles are capable of faster speeds so they have much larger ranges of particle speeds.

Middling

Looking at the graph above from the prior example, what will have a larger speed distribution, helium at 500 K or argon at 250 K? Helium at 300 K or argon at 400 K? Argon at 400 K or argon at 900 K?

This problem requires some intuition.

Looking at the first case, helium at 500 K will probably have the larger speed distribution because the temperature is much higher than argon's temperature, and looking at the graph, it can be inferred that helium particles are lighter than argon particles. This allows helium particles to achieve a larger range of speeds.

For the second case, it seems to be that helium particles will still have a larger speed distribution even though the helium particles are exposed to a lower temperature (300 K) than argon particles (400 K). This is again due to the light helium particles that make up for the lower temperature.

For the third case, the larger speed distribution will occur for argon at 900 K because higher temperatures will cause particles to move at faster speeds, thus forming a larger speed distribution.

Difficult

Using the Maxwell-Boltzmann function, calculate the number of helium gas particles in a sample of 100,000 helium particles with a speed of 325 m/s at 500K. Given that [math]\displaystyle{ m_{helium} = 6.65 × 10^{-27} kg }[/math] and [math]\displaystyle{ k = 1.381 × 10^{-23} m^2*kg*s^{-2}*K^{-1} }[/math].

Given the Maxwell-Boltzmann function:

[math]\displaystyle{ f(v) = \sqrt{\left(\frac{m}{2 \pi kT}\right)^3}\, 4\pi v^2 e^{- \frac{mv^2}{2kT}}, }[/math]

We have been given the values of T, v, [math]\displaystyle{ m_{helium} }[/math], and [math]\displaystyle{ k }[/math]. From here, we can plug these values into the formula.

[math]\displaystyle{ f(325) = \sqrt{\left(\frac{(6.65 × 10^{-27})}{(2 \pi)(1.381 × 10^{-23})(500)}\right)^3}\, 4\pi (325)^2 e^{- \frac{(6.65 × 10^{-27})(325)^2}{2(1.381 × 10^{-23})(500)}}, }[/math]

[math]\displaystyle{ f(325) = .0000755 }[/math]

Number of Helium Particles [math]\displaystyle{ = f(325)*(100,000) = 7.55 }[/math]

Based on this fraction, if there were 100,000 helium particles, there would only be between 7 or 8 particles with this speed at this temperature. This is a very small fraction of helium particles.

Connectedness

This topic is particularly interesting to me because of its potential use in my father's work. My father is a chemist, and often he has to induce reactions involving gases. When I read about this topic, it was really interesting to see how one can calculate the speeds of particles based on these distributions. This is important because from this one can calculate the energy of a single gas particle, and this could be important if a scientist like my father needed a specific energy level. It was just really interesting to see how mass, speed, and temperature of a system all have an important relationships with each other. This is not a huge connection to my major (Mechanical Engineering) as it seems to be more related to chemical engineering, but I would like to learn more about this concept in other classes. There are some applications for scientists to use these Maxwell-Boltzmann Distributions as guides to induce reactions between particles.

History

In 1857, a scientist by the name of Rudolf Clausius figured out how to calculate the speed of atoms. A few years later, in 1860, Irish physicist James Maxwell published a paper, in which he ascertained a way to connect the physical properties of gases to the distribution of particle velocities. His research compounded off of Clausius's work, but he went further by describing the distribution of speeds in reference to the average speed. In 1872, Austrian physicist, Ludwig Boltzmann, substantiated Maxwell's research by adding the H-theorem, which quantified the approach to equilibrium at which the Maxwell distribution velocities exist. Because of Maxwell and Boltzmann's collaboration, they had come up with a function called the Maxwell-Boltzmann Distribution.

See also

The Energy Principle Kinetic Energy

Further reading

Matter and Interactions, Volume I, Modern Mechanics

External links

[1] [2]

References

Blauch, D. (2014). Kinetic Molecular Theory. Retrieved December 5, 2015, from http://www.chm.davidson.edu/vce/kineticmoleculartheory/Maxwell.html

Burton, T. (1999, April 25). The Maxwell-Boltzmann distribution. Retrieved December 5, 2015, from http://dwb.unl.edu/teacher/nsf/c09/c09links/www.kobold.demon.co.uk/kinetics/maxboltz.htm

Chabay, R., & Sherwood, B. (2011). Entropy: Limits on the Possible. In Matter and Interactions (3rd ed., Vol. 1, pp. 839-842). Hoboken: Wiley.

Maxwell-Boltzmann Distributions. (2013, October 2). Retrieved December 5, 2015, from http://chemwiki.ucdavis.edu/Physical_Chemistry/Kinetics/Rate_Laws/Gas_Phase_Kinetics/Maxwell-Boltzmann_Distributions

Search Results - Hmolpedia. (n.d.). Retrieved December 5, 2015, from http://www.eoht.info/page/Maxwell-Boltzmann distribution

Main Category: Energy