Energy of a Single Particle

Elif Kulaksizoglu Fall 2019

Introduction

We are going to take a side step from the macroscopic world for a moment, and focus on the energy of very small particles - particles like protons, neutrons and electrons. Because of revolutions in modern physics in the last two centuries, we know that these particles act differently than objects in the macroscopic world - in fact, any object that can move close to the speed of light will behave differently than most objects we encounter in our daily life. Because of this, we need different ways of calculating the energy associated with them.

There are two types of energy these particles can have: rest energy and kinetic energy. Rest energy is, as you might expect, the energy of the rest mass of a particle. Kinetic energy, as we have seen before, is the energy associated with the motion of a particle. Calculations associated with these energies are usually very simple, so pay attention to the equations and units and you should be fine.

The formulas for calculating rest energy and kinetic energy may look familiar to you. That is because they are a lot like the formulas used to compute the energy of macroscopic quantities. The only main difference you may notice immediately is there is a γ (gamma) in those equations. That gamma is a Lorentz Factor, which is used to make relativistic corrections as a particle approaches the speed of light. You'll notice in the formula for gamma (shown below) that as the ratio of the particle speed to the speed of light approaches zero, γ approaches 1. Then, the formulas look exactly like the ones you are used to!

Relativistic Energy Equations
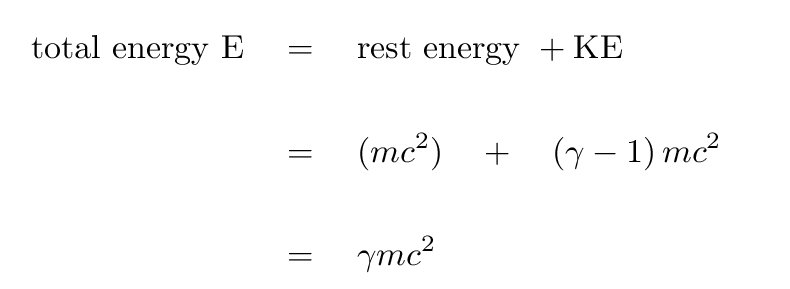
(see ref. 1)

A Mathematical Model

Types of point particles:

• 1. Electrons
• 2. Protons
• 3. Neutrons

Masses of point particles:

• 1. Electron mass = 9.109 e -31 kg
• 2. Proton mass = 1.6726 e -27 kg
• 3. Neutron mass = 1.6750 e -27 kg
  
  

There are three equations to look at that were discussed above:

Relativistic Correction (Lorentz) Factor

[math]\displaystyle{ γ = 1/ \sqrt{1-(v^2/c^2)} }[/math] where v is the velocity of the particle and c is the speed of light

Rest Energy of a particle

[math]\displaystyle{ E_{Rest}=mc^2 }[/math] - Rest Energy, where m is the mass and c is the speed of light. This type of energy describes the inherent energy contained within an object arising from chemical makeup. Rest energy will only ever change if the system being observed is at an atomic level where particles tends to change identities spontaneously during interactions with surroundings.

Kinetic Energy of a particle nearing the speed of light

[math]\displaystyle{ E_{Kinetic}=γmc^2-mc^2 }[/math] - Where γ is as calculated above, m is the mass of the particle and c is the speed of light

The combined energy equation

[math]\displaystyle{ E_{Particle}=γmc^2 }[/math]
Where γ is as calculated above, m is the mass of the particle and c is the speed of light

A Computational Model

Examples

A proton moves at 0.950c. 
Calculate its (a) rest energy, (b) total energy, and (c) kinetic energy. 

• (a) [math]\displaystyle{ E_{rest}=mc^2 }[/math] = (1.67e-27 kg)(3e8 m/s)^2 = 1.5e-10 J
• (b) [math]\displaystyle{ E_{particle}=γmc^2 }[/math] = (1.5e-10 J)/((1-(0.950c/c)^2)^(1/2)) = 4.81e-10 J
• (c) [math]\displaystyle{ K=γmc^2-mc^2 }[/math] = 4.81e-10 J - 1.50e-10 J = 3.31e-10 J

An electron is accelerated to a speed of 2.95 × 108
(a) What is the energy of the electron?  
(b) What is the rest energy of the electron? 
(c) What is the kinetic energy of the moving proton?

(a)
E = γmc²
E = (5.50)(9.11 × 10^-31)(3 × 10⁸)
E = 1.50 × 10^-21 J
(b)
E_rest = mc²
E_rest = (9.11 × 10^-31)(3 × 10⁸)²
E_rest = 2.73 × 10^-22 J
(c)
K = E - E_rest
K = 1.50 × 10^-21 - 2.73 × 10^-22
K = 1.23 × 10^-21 J

Connectedness

1. How does modern relativity modify the law of conservation of energy?

According to modern relativity, the relativistic momentum of a particle can be defined as p = γmv for velocities that are near the speed of light. This is also the same thing as multiplying classical momentum, p = mv, by the relativistic factor γ. Relativistic momentum approaches infinity as the particle’s speed approaches c, the speed of light. This indicates that a particle will never reach the exact speed of light no matter how close it can get to it. This prevents its momentum from becoming infinite. As it is seen from the graph, as v approaches c, the momentum value goes to positive infinity, but never actually becomes infinity, which proves the law of conservation of momentum true. If the momentum value had reached infinity, then we wouldn’t be able to make a conclusion about the conservation of momentum. Thus, it we would also be unable to make a claim about the conservation of energy since it is related to momentum.

2. Is it possible for an external force to be acting on a system and relativistic momentum to be conserved? Explain.

Even if there is an external force acting on a system, if there are additional external forces that balance this force out, the net external force will be zero, and the relativistic momentum will be conserved. If the net external force is zero, this means that the acceleration of the system will also be zero. Zero acceleration means that the initial and final values for the velocity of the system are the same. This leads to a momentum value that does not change throughout the process, assuming that the mass of the system is kept the same. In this case, we can conclude that if there is an external force acting on a system, the relativistic momentum can still be conserved as long as the net external force is zero.

3. Given the fact that light travels at c, can it have mass? Explain.

We know that c, the speed of light, is equal to 3E10^8 m/s. According to Maxwell’s equation, any object with mass m cannot travel with the speed of light or greater. Therefore, we conclude that if light travels at c, than it should not have a mass.

4. We know that the velocity of an object with mass has an upper limit of c. Is there an upper limit on its momentum? Its energy? Explain.

Neither the momentum nor the energy has an upper limit. The relativistic momentum is given by p = γmu, and the total energy is given by E = γmc^2. We know that γ approaches infinity as v approaches the speed of light, c. Looking at the equations, we see that γ is directly proportional to both momentum and total energy. As γ tends to infinity, momentum and total energy tend to infinity as well. Therefore, it can be concluded that there is no upper limit to neither of them.

History

ADD HISTORY INFO HERE

More Info

(1) http://spiff.rit.edu/classes/phys150/lectures/ke_rel/ke_rel.html