Spring Potential Energy

CLAIMED BY Taraji Long Fall 2019 11/15/2019 This topic covers Spring Potential Energy.

The Main Idea

Spring Potential Energy

Spring potential energy, also known as elastic potential energy,is the stored energy in a spring, that can potentially be converted into kinetic energy. The energy stored in the spring is due to the deformation of the spring, often from stretching and compressing. The force excreted to stretch or compress a spring is known as Hooke's law, F_s = -k_xs, where F_s is force, x is the displacement, and -k_s is the spring constant. The spring constant being unique for every spring depends on factors such as material and thickness of coiled wire. If a spring is not stretched or compressed, then it is at equilibrium. At equilibrium a spring has no potential energy, assuming there is no force being applied to the spring.

A Mathematical Model

The formula for Force of a Spring:

F_s = -k_sx

The formula for Spring Potential Energy:

U_s = ¹⁄₂k_sx²

where:

k_s = spring constant

x² = stretch measured from the equilibrium point;

A Computational Model

An oscillating spring on the floor:

GlowScript 2.9 VPython
display(width=600,height=600,center=vector(6,0,0),background=color.black)
mbox=2  
L0 = vector(9,0,0) 
ks = 1   
deltat = .01  
t = 0    
wall=box(pos=vector(0,1,0),size=vector(0.2,3,2),color=color.cyan)
floor=box(pos=vector(7.2,-0.6,0),size=vector(14,0.2,4),color=color.cyan)
box=box(pos=vector(12,0,0),size=vector(1,1,1),color=color.red)
pivot=vector(0,0,0)
spring=helix(pos=pivot,axis=box.pos-pivot,radius=0.4,constant=1,thickness=0.1,coils=20,color=color.orange)
box.p = vector(0,0,0)
while (t<50):
 rate(100)
 s = wall.pos - box.pos
 Fspring=(L0-box.pos)*(ks)
 box.p= box.p +Fspring*deltat
 box.pos = box.pos + box.p*deltat
 spring.axis = box.pos - spring.pos
 t = t+ deltat

Link to Simulation: https://trinket.io/glowscript/3146b836dc

An hanging oscillating spring:

from __future__ import division                
from visual import *
from visual.graph import *
scene.width=600
scene.height = 760
g = 9.8
mball = .2
Lo = 0.3    
ks = 12    
deltat = 1e-3
t = 0       
ceiling = box(pos=(0,0,0), size = (0.5, 0.01, 0.2))
ball = sphere(pos=(0,-0.3,0), radius=0.025, color=color.yellow)
spring = helix(pos=ceiling.pos, color=color.green, thickness=.005, coils=10, radius=0.01)
spring.axis = ball.pos - ceiling.pos
vball = vector(0.02,0,0)
ball.p = mball*vball
scene.autoscale = 0            
scene.center = vector(0,-Lo,0)   
while t < 10:           
 rate(1000)    
 L_vector = (mag(ball.pos) - Lo)* ball.pos.norm()
 Fspring = -ks * L_vector
 Fgrav = vector(0,-mball * g,0)
 Fnet = Fspring + Fgrav
 ball.p = ball.p + Fnet * deltat
 ball.pos = ball.pos + (ball.p/mball) * deltat
 spring.axis = ball.pos-ceiling.pos  
 t = t + deltat

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Question

If a spring's spring constant is 200 N/m and it is stretched 1.5 meters from rest, what is the potential spring energy?

Solution

k_s= 200 N/m

s= 1.5 m

U_s=(0.5)k_ss²

U_s= (0.5)(200 N/m)(1.5 m)²

U_s= 225 J

Middling

Question

A horizontal spring with stiffness 0.6 N/m has a relaxed length of 10 cm. A mass of 25 g is attached and you stretch the spring to a length of 20 cm. The mass is released and moves with little friction. What is the speed of the mass at the moment when the spring returns to its relaxed length of 10cm?

Solution

k_s= 0.6 N/m

s= 0.1 m

U_s=(.5)k_ss² = (.5)(0.6 N/m)(0.1 m)²

U_s = 0.003 J

Potential Energy is Converted into Kinetic Energy (K):

U_s = K

U_s =(0.5)mv²

0.003 J = (0.5)(0.025 kg)v²

v² = ^{(0.003 J)}⁄_{((0.5)(0.025 kg))}

v² = 0.24 J/kg*s

v = 0.49 m/s

Difficult

Question

A package of mass 9 kg sits on an airless asteroid with mass 8.0x10²⁰ kg and radius 8.7x10⁵ m. Your goal is to launch the package so that it will never come back and when it is very far away it will have a speed of 226 m/s. You have a spring whose stiffness is 2.8x10⁵ N/m. How much must you compress the spring?

Solution

The initial condition for escape from the asteroid is:

K_i+U_i=¹⁄₂mv_esc² + (-G*^Mm⁄_R)=0

Potential energy of the spring equals the total energy in the system.

¹⁄₂k_ss²=¹⁄₂mv_esc² +(-G*^Mm⁄_R)

s²= ^m⁄_ks(^2GM⁄_R +v²)=s² = ⁹⁄_2.8x10⁵(^2G8.0x1020⁄_8.7x10⁵+226²)

s²=5.58 m

s=2.36 m

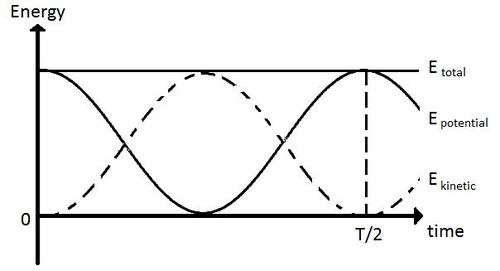
Graphing

Energy graph

The energy graph of a oscillating spring continuously switches between kinetic and potential energy because springs are continuously returning to equilibrium.

Connectedness

Because springs are all around us, from Slinkies to parts in automobiles, spring potential energy is useful in everyday life. One example of this is a trampoline. Without potential spring energy to allow for bounce, a trampoline would simply be a boring stretch of fabric. Spring potential is also used to absorb shock in vehicles. This allows for a smoother ride while traveling over bumps in the road.

Trampoline Potential Energy

History

Elastic Potential Energy stemmed from the ideas of Robert Hooke, a 17th century British physicist who studied the relationship between forces applied to springs and elasticity. Hooke’s Law, which is a principle that states that the that the force needed to extend or compress a spring by a distance is proportional to that distance.

See also

Spring potential energy is related to Hooke's Law and Potential Energy.

Further reading

http://hyperphysics.phy-astr.gsu.edu/hbase/pespr.html

External links

[1]

References

1. http://www.universetoday.com/55027/hookes-law/
2. http://www.scienceclarified.com/everyday/Real-Life-Physics-Vol-2/Oscillation-Real-life-applications.html
3. http://hyperphysics.phy-astr.gsu.edu/hbase/pespr.html
4. Chabay and Bruce A. Sherwood. Matter & Interactions. 4th ed.