Current in an LC Circuit: Difference between revisions

Revision as of 23:25, 13 April 2025

CLAIMED BY: Rafay Hadi (Spring 2025)

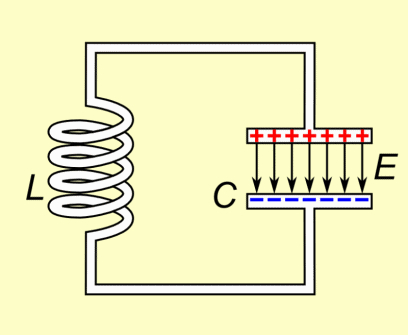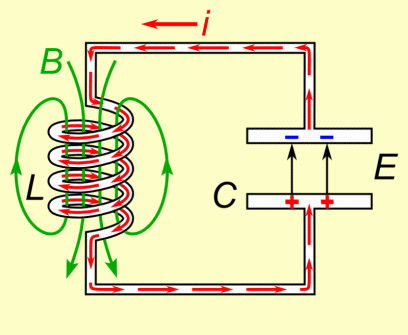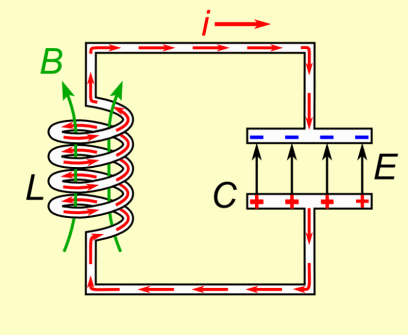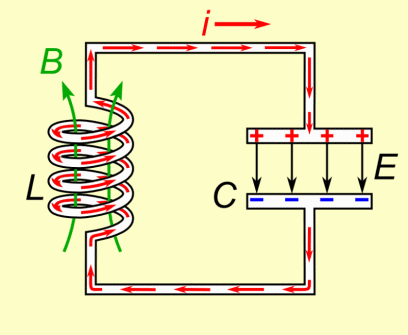
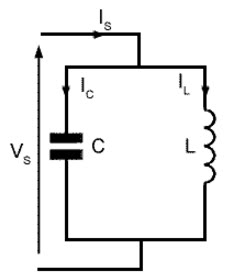
An LC circuit contains an inductor and a capacitor, and because of the inductor's sluggishness and resistance to change the current, the charge in this circuit can oscillate back and forth forever. The inductor is represented by the letter L and the capacitor by the letter C, and these are connected together in a circuit to create and LC circuit. You should already know that a capacitor stores energy in an internal electric field while an inductor stores energy in a surrounding magnetic field. If you have a closed switch, such as in the image below, the voltage across the capacitor(C) is applied to the inductor (L). At this moment, C begins to discharge itself through L. However, the current through L cannot change instantaneously, and the voltage across C cannot change instantaneously. So the current through L (and C) increases gradually as the voltage across C (and L) decreases gradually. There is no resistance present in this circuit, so there is no loss of energy, and rather the rate at which C discharges itself through L increases, and it increases the current through L.

The Main Idea

An LC circuit is a fundamental building block in electronics, consisting of just two components: an inductor (L) and a capacitor (C), connected in a closed loop. These components store energy in different ways—capacitors store energy in electric fields, while inductors store energy in magnetic fields. When connected together, they create an oscillating system where energy shifts back and forth between these two forms.

How It Works

Initially, the capacitor is fully charged. When a switch closes, it begins to discharge, releasing energy into the circuit. However, the inductor resists sudden changes in current (a property known as inductance), so the current doesn't jump instantly to a high value—it increases gradually. As the capacitor discharges, the energy it stored is transferred into the magnetic field of the inductor.

Once the capacitor is fully discharged, the current is at its maximum. But the inductor doesn’t allow the current to stop abruptly, so it keeps pushing current through the circuit—recharging the capacitor with opposite polarity. This starts the cycle in reverse.

This back-and-forth exchange of energy continues in a sinusoidal oscillation pattern. In an ideal LC circuit with no resistance, this oscillation would continue forever.

At the moment the capacitor runs out of charge, there is a current in the inductor, and because inductors are sluggish by nature, the current can't immediately change to zero. Therefore, the system does not come to equilibrium and instead increases the charge in the capacitor. When the capacitor is fully charged, it starts to discharge back through the inductor, and the process repeats. Since the circuit will never reach equilibrium and current never reaches zero, this oscillating process repeats forever. Oscillations could reach a stopping point if there is some resistance, but it may still go through multiple cycles before equilibrium is reached.

Why this is special

A series LC circuit—where the inductor and capacitor are connected end-to-end—exhibits behaviors that differ from non-oscillating circuits. For example:

In RC circuits, voltage or charge decays exponentially toward equilibrium.

In LC circuits, charge and current vary periodically, resembling sine or cosine functions.

Because energy is conserved and exchanged smoothly between the inductor and capacitor, LC circuits can oscillate continuously if resistance is small. That’s why LC circuits typically use low-resistance, thick copper wires to minimize energy loss.

A Mathematical Model

An LC circuit has an energy conservation rule associated with it. The energy conservation loop rule for an LC circuit is: [math]\displaystyle{ \Delta V_{capacitor} + \Delta V_{inductor} = \frac{Q}{C}-L\frac{dI}{dt} = 0 }[/math] where [math]\displaystyle{ Q }[/math] is the charge on the upper plate of the capacitor and [math]\displaystyle{ I }[/math] is the conventional current leaving the upper plate and going through the inductor.

[math]\displaystyle{ dQ/dt }[/math] is the amount of charge flowing off the capacitor every second. This is the same as the current. Because the charge is leaving the capacitor, [math]\displaystyle{ I = -\frac{dQ}{dt} }[/math].

Energy conservation can be re-written as [math]\displaystyle{ \frac{1}{C}Q+L\frac{d^{2}Q}{dt^{2}} = 0 }[/math]

In addition, by substituting Q and its second derivative into the equation, a possible solution of the rewritten energy conservation equation is [math]\displaystyle{ Q = Q_{i}cos(\frac{1}{\sqrt{LC}}t) }[/math]

Therefore, the current is given by: [math]\displaystyle{ I = -\frac{dQ}{dt} = \frac{Q_{i}}{\sqrt{LC}}sin(\frac{1}{\sqrt{LC}}t) }[/math]

A Computational Model

Summary and Applications

Some synonyms commonly used for an LC circuit include tank circuit, tuned circuit, and resonant circuit—all highlighting its key role in frequency selection and oscillation.

An LC circuit is an electric circuit composed of a capacitor (C) and an inductor (L) connected together. These circuits naturally oscillate at a specific frequency determined by the values of L and C. This resonant frequency allows LC circuits to either generate signals at that frequency or selectively respond to signals within a broader spectrum.

Because of this frequency-selective behavior, LC circuits are central to many electronic systems. They are commonly used in:

Radio receivers and transmitters, where they tune into specific frequencies while filtering out others

Bandpass filters, which allow only a certain range of frequencies to pass through

Oscillators, which generate stable sine wave signals used in clocks, radios, and signal generators

Voltage and current magnifiers, where they amplify resonant signals at specific frequencies

Impedance matching circuits, to maximize power transfer between components

Induction heating systems, where oscillating currents generate high-frequency magnetic fields for heating metal

They also appear in RF (radio frequency) and analog signal processing applications, forming the basis of resonant amplifiers, frequency modulators, and spectrum analyzers.

In summary, LC circuits are fundamental to frequency control, waveform generation, and energy transfer, making them a backbone of modern electronic communication and signal-processing systems.

Comparison to a Spring

As stated above, An LC circuit is a closed electrical loop made up of just two components: a capacitor (C) and an inductor (L). Like a mass on a spring, this system exhibits resonance—there’s a natural frequency at which it prefers to oscillate, and when driven at that frequency, it responds with large amplitude oscillations.

In this circuit, electric charge oscillates back and forth, much like how a mass oscillates around an equilibrium position on a spring. The analogy extends to the key parameters that define each system:

Mass 𝑚 is analogous to inductance 𝐿

Spring displacement 𝑥 is analogous to charge 𝑄

Velocity 𝑣=𝑑𝑥/𝑑𝑡 corresponds to current 𝐼=𝑑𝑄/𝑑𝑡

Spring stiffness 𝑘 relates to the inverse of capacitance 1/𝐶

Just as a spring-mass system has a natural frequency [math]\displaystyle{ \omega = \sqrt{\frac{k}{m}} }[/math], an LC circuit resonates at a characteristic angular frequency

[math]\displaystyle{ \omega = \frac{1}{\sqrt{LC}} }[/math]

This is the frequency at which the circuit most efficiently exchanges energy between the electric field in the capacitor and the magnetic field in the inductor.

Examples

Use the given circuit and information to solve for the following quantities:

L = 4.0 mH

C = 5.0 μF

Simple

Find the resonant frequency in radians per second and Hertz and the period in seconds:

Middling

Find the initial charge on the fully charged capacitor and the maximum current between oscillations:

Connectedness

This topic is connected to RC circuits, which approach equilibrium slowly, as well as RL circuits, which approach steady state current slowly. However, an LC circuit is an example of a circuit that oscillates, where charge moves back and forth forever, and never settles to an equilibrium or steady state.

As an engineer, these circuits can be useful in many areas, particularly to electrical and mechanical engineers. A common applications is tuning radio transmitters and receivers.When we tune a radio to a particular station, the LC circuits are set at a resonance for that particular carrier frequency.

LC circuits can also be applied to voltage magnification and current magnification. LC circuit can additionally be used in induction heating.

Parallel and Series

Series is shown below

Parallel is shown below

History

In 1826, French scientist Felix Savary was the first to discover evidence that a capacitor and an inductor could produce electrical oscillations. In his experiment, he discharged a Leyden jar through a wire wound around an iron needle. He found that sometimes the needle was left magnetized in one direction and other times it was in the opposite direction. He concluded that this was due to a damped oscillating discharge current in the wire, which reversed the magnetization of the needle back and forth until it was too small to have an effect, leaving the needle magnetized in a random direction.

Then in 1889, there was one of the first demonstrations of resonance with Lodge's "syntonic jars" experiment. In this experiment, two resonant circuits were next to each other, and each consisted of a Leyden jar connected to a one-turn coil with a spark gap. If a high voltage from the induction coil was then applied to one of the circuits, then sparks were excited in the other tuned circuit only when the circuits were adjusted to resonance.

LC circuits first practical use began around 1890 with spark-gap radio transmitters to allow the receiver and transmitter to be tuned to the same frequency. The first patent for a radio system that allowed tuning was filed by Lodge in 1897, and systems were invented in 1900 by Italian radio pioneer Guglielmo Marconi.

Applications

The LC circuit has many applications:

-signal processing and communications systems

-Tuning radio transmitters and receivers

-A series resonant circuit can be used for voltage magnification

-A parallel resonant circuit provides current magnification

-Both parallel and series can be used in induction heating

LC circuits can also be electronic resonators for use in things like amplifiers, oscillators, tuners, and more.

References

Matter & Interactions 4th Edition: Electric and Magnetic Interactions

http://www.chegg.com/homework-help/questions-and-answers/x-i5rong-please-help-part-g-learning-goal-understand-processes-series-circuit-containing-i-q74127

https://en.wikipedia.org/wiki/LC_circuit

http://farside.ph.utexas.edu/teaching/315/Waves/node5.html

http://physics.info/circuits-rlc/

https://www.youtube.com/watch?v=v3-HwZMThzQ

https://www.youtube.com/watch?v=_8d4LQMFc1o