Potential Difference in an Insulator

Potential difference is defined as a scalar quantity that measures the difference of energy per unit charge. This page will not go over how to calculate electric potential in a conductor (because other pages cover this topic), but rather, how to find the electric potential in an insulator given the potential difference in a vacuum.

Potential Difference

Although this section will not go in depth into how to calculate potential difference, the following analysis requires the knowledge that potential difference equals the dot product of the electric field vector and distance vector between two points. Understanding that potential difference is dependent on the distance between two points is an important prerequisite to comprehending how to find the potential difference inside an insulator.

Net Electric Field Inside an Insulator

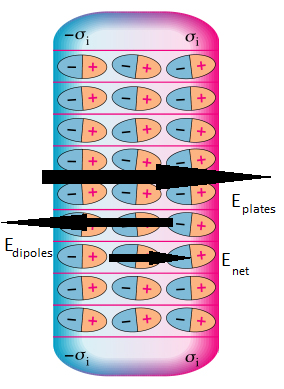
Between two points inside a metal object in equilibrium, the potential difference is zero. However, this is untrue for an insulator that is polarized by an applied electric field (such as that inside a capacitor). In order to quantitatively predict the potential difference between two points in an insulator, we first must understand how this applied electric field polarizes molecules in the surrounding objects. Typically, this electric field creates induced dipoles inside the insulating materials. These induced dipoles contribute their own electric field to the net field. Because dipoles create such a unique pattern of electric field, it is slightly more complex to find the electric field and potential difference inside the insulator.

The net electric field inside the insulating material is the sum of the applied electric field (often due to a capacitor) and the electric field produced by the induced dipoles. The field from the induced dipoles always points in the direction opposite to the applied electric field (as shown in Diagram 1). Consequently, the net electric field is in the direction of the applied field/capacitor, but it is weaker in magnitude.

Dielectric Constant

When solving for the potential difference in an insulator, we define the constant K as the dielectric constant. This quantity represents the amount by which the net electric field is "weakened" due to the induced dipoles. It is a value typically known through previous scientific experimentation (specifically, measuring the effect of an insulator on the potential difference between two charged objects).

A Mathematical Model for the Electric Field Inside an Insulator

[math]\displaystyle{ \vec {E}_{insulator} = \frac{\vec{E}_{applied}}{K} }[/math]

The dielectric constant K is always bigger than one if an insulator is present because the induced dipoles in the polarized insulator always weaken the net electric field. When an insulating substance is easy t polarize, K will be large because the induced dipoles will create a weaker net electric field. If there is no insulating material between the charged objects (the space is a vacuum), K equals one.

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Relating Electric Field to Potential Difference

Because the relationship between the electric field and potential difference is proportional, potential difference will also decrease by a value K. That is, placing an insulator in between two charged objects like the plates of a capacitor also decreases potential difference across the insulator. It is important to note that if the insulator does not fill the gap between objects, the electric field and potential difference inside the insulator are still reduced by a factor K. However, the areas that are not filled by the insulator are not affected since the electric field inside the insulator is negligibly small.

A Mathematical Model for the Potential Difference Inside an Insulator

[math]\displaystyle{ \Delta{V}_{insulator} = \frac{\Delta{V}_{vacuum}}{K} }[/math]

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

A capacitor is known to create a uniform electric field of magnitude 200 N/C. The capacitor plates are 5mm apart. A plastic slab (whose dielectric constant is 5) is carefully inserted into the gap between the capacitor. Calculate the potential difference across the insulator.

Solution: [math]\displaystyle{ \Delta{V}_{insulator} = \frac{\Delta{V}_{vacuum}}{K} }[/math]

Connectedness

This topic is important in analyzing circuits (particularly RC circuits).

1. How is it connected to your major?
2. Is there an interesting industrial application?

History

Potential difference is a phenomenon that was first discovered by Alessandro Volta, an Italian physicist who lived from 1745 to 1827. Through his work with Luigi Galvani, Volta detected the flow of electric current through various conducting materials. This led to the discovery of electromotive force (what we more commonly refer to as emf) and eventually allowed Volta to create the first battery. Slightly later, Georg Ohm, a German physicist, began studying Volta's research. Through experimentation, Ohm was the first to uncover the relationship between the potential difference applied through a conductor and the resultant electric current. These findings and scientists were the most crucial to discovering the relationships between current, resistance, electric field, and voltage/potential difference.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

http://www.physics.sjsu.edu/becker/physics51/capacitors.htm

-cbrogan7