Spring Motion: Difference between revisions
mNo edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
==Spring Motion== | ==Spring Motion== | ||
While the momentum you have dealt with before may have followed a linear path based on a constant force, spring motion is involved with a changing net force. As you may have noticed when trying to compress or stretch a helical spring, it resists motion (with high opposing force) most when its length is farthest from the relaxed length in either direction. | |||
This force alone would indicate a movement along the length and direction of the spring, oscillating based on the addition of a mass. | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
The Force due to a spring follows the relationship <math> F_{spring} = -k_s*s*L_{hat} </math> | |||
where <math> k_s </math> is the specific stiffness of the spring, <math> s </math> is the change in length of the spring from the current to the relaxed length <math> s= L - L_0 </math> and <math> L_{hat} </math> is the unit vector indicating the direction of the vector pointing from the spring's origin to the mass. | |||
Spring motion can be predicted using the momentum principle <math> dp=F_{net}*dt </math> and the position-update formula <math> dr= p_f/m*dt </math> Because spring motion involves oscillation, it is important to iterate with a small enough change in time to capture the full path of the spring-mass system. | |||
===A Computational Model=== | ===A Computational Model=== | ||
Follow the link to check out a 3D model of Spring Motion. The code displays a spring with one fixed end on a ceiling and a mass attached to the free end. | |||
https://trinket.io/glowscript/3587ff8cbe | |||
The pink arrow represents the magnitude and direction of the mass's momentum. | |||
The yellow arrow represents the changing net force, Force of gravity + Force of the spring, on the mass (scaled down to 10%). | |||
Examine the orange curve after the simulation ends to follow the path of the mass's motion. | |||
Try an initial mass location to give a straight vertical path! | |||
=Simple Example= | =Simple Example= | ||
Revision as of 01:32, 1 December 2015
by Caroline Ware
Spring Motion
While the momentum you have dealt with before may have followed a linear path based on a constant force, spring motion is involved with a changing net force. As you may have noticed when trying to compress or stretch a helical spring, it resists motion (with high opposing force) most when its length is farthest from the relaxed length in either direction. This force alone would indicate a movement along the length and direction of the spring, oscillating based on the addition of a mass.
A Mathematical Model
The Force due to a spring follows the relationship [math]\displaystyle{ F_{spring} = -k_s*s*L_{hat} }[/math] where [math]\displaystyle{ k_s }[/math] is the specific stiffness of the spring, [math]\displaystyle{ s }[/math] is the change in length of the spring from the current to the relaxed length [math]\displaystyle{ s= L - L_0 }[/math] and [math]\displaystyle{ L_{hat} }[/math] is the unit vector indicating the direction of the vector pointing from the spring's origin to the mass.
Spring motion can be predicted using the momentum principle [math]\displaystyle{ dp=F_{net}*dt }[/math] and the position-update formula [math]\displaystyle{ dr= p_f/m*dt }[/math] Because spring motion involves oscillation, it is important to iterate with a small enough change in time to capture the full path of the spring-mass system.
A Computational Model
Follow the link to check out a 3D model of Spring Motion. The code displays a spring with one fixed end on a ceiling and a mass attached to the free end. https://trinket.io/glowscript/3587ff8cbe The pink arrow represents the magnitude and direction of the mass's momentum. The yellow arrow represents the changing net force, Force of gravity + Force of the spring, on the mass (scaled down to 10%). Examine the orange curve after the simulation ends to follow the path of the mass's motion. Try an initial mass location to give a straight vertical path!
Simple Example
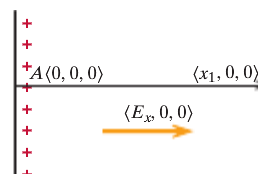
In this example, the electric field is equal to [math]\displaystyle{ E = \left(E_x, 0, 0\right) }[/math]. The initial location is A and the final location is C. In order to find the potential difference between A and C, we use [math]\displaystyle{ dV = V_C - V_A }[/math].
Since there are no y and z components of the electric field, the potential difference is [math]\displaystyle{ dV = -\left(E_x*\left(x_1 - 0\right) + 0*\left(-y_1 - 0\right) + 0*0\right) = -E_x*x_1 }[/math]
Let's say there is a location B at [math]\displaystyle{ \left(x_1, 0, 0\right) }[/math]. Now in order to find the potential difference between A and C, we need to find the potential difference between A and B and then between B and C.
The potential difference between A and B is [math]\displaystyle{ dV = V_B - V_A = -\left(E_x*\left(x_1 - 0\right) + 0*0 + 0*0\right) = -E_x*x_1 }[/math].
The potential difference between B and C is [math]\displaystyle{ dV = V_C - V_B = -\left(E_x*0 + 0*\left(-y_1 - 0\right) + 0*0\right) = 0 }[/math].
Therefore, the potential difference A and C is [math]\displaystyle{ V_C - V_A = \left(V_C - V_B\right) + \left(V_B - V_A\right) = E_x*x_1 }[/math], which is the same answer that we got when we did not use location B.
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page