The Moments of Inertia: Difference between revisions
| Line 52: | Line 52: | ||
::::::::<math>I = 2 \cdot (2.3 \times 10^{-26} kg)(0.75 \times 10^{-10} m)^2 </math> | ::::::::<math>I = 2 \cdot (2.3 \times 10^{-26} kg)(0.75 \times 10^{-10} m)^2 </math> | ||
::::::::<math>I = 2.6 \times 10^{-46} kg \cdot m^2</math> | ::::::::<math>I = 2.6 \times 10^{-46} kg \cdot m^2</math> | ||
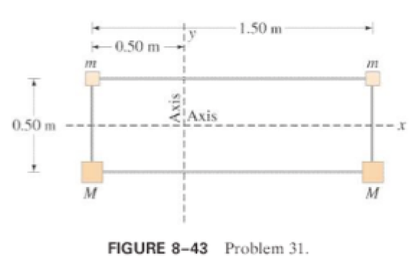
'''2. '''Calculate the moment of inertia of the array of point masses shown in figure 8-43 below. Assume m=1.8 kg and M=3.1 kg and the objects are wired together by very light, rigid pieces of wire. The array is rectangular with the dimensions indicated. The horizontal axis splits the 0.50 m distance in half. The vertical axis is 0.50 m from the left side of the rectangle. [http://www.hunter.cuny.edu/physics/courses/physics110/repository/files/Giancoli_Prob.Solution%20Chap.8.pdf] | '''2. '''Calculate the moment of inertia of the array of point masses shown in figure 8-43 below. Assume m=1.8 kg and M=3.1 kg and the objects are wired together by very light, rigid pieces of wire. The array is rectangular with the dimensions indicated. The horizontal axis splits the 0.50 m distance in half. The vertical axis is 0.50 m from the left side of the rectangle. [http://www.hunter.cuny.edu/physics/courses/physics110/repository/files/Giancoli_Prob.Solution%20Chap.8.pdf] | ||
Revision as of 16:50, 1 December 2015
claimed and written by san47
Moment of Inertia is a factor in rotational kinetic energy and angular momentum and the fundamental principle - conservation of angular momentum. It is the rotational analog of mass which when multiplied by angular acceleration equals net torque in Newton's 2nd Law for Rotation which is one example of several Rotation-Linear Parallels. Rotation-Linear Parallels are part of the description of rotational motion. The moment of inertia for a point mass can be expressed as [math]\displaystyle{ I=mr^2. }[/math] It is accounting for the mass distribution. [1]
Definition
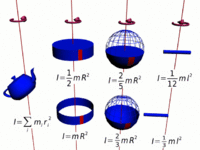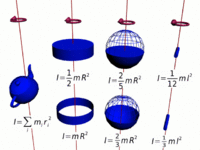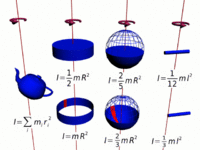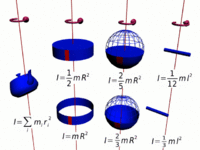
Moment of inertia, denoted by the letter I, is another name for rotational inertia. It is associated with an object that is rotating about its center, or an axis by measuring how hard it is to change an objects rotation rate. The moment of inertia for any rotating objects must be specified with respect to a chosen axis of rotation due to the varying distance r. The moment of inertia corresponds to mass for translational/linear motion. [2][3]
A Mathematical Model

The moment of inertia is the sum of mass times the square of perpendicular distance to the rotation axis, that is [math]\displaystyle{ I=\Sigma mr^2 }[/math]for all point mass components. This relationship is the basis for all other moments of inertia since any object can be a collection of point masses.[4] Note that I has units of mass multiplied by distance squared (kg⋅m2), as we might expect from its definition.
Calculating Moment of Inertia

Thin Rod
Divide into Small Slices Divide the rod into N small slices of equal length [math]\displaystyle{ \Delta x = L/N }[/math], each with mass of [math]\displaystyle{ \Delta M = M/N }[/math].
The Mass of One Slice Concentrate on one representative slice: [math]\displaystyle{ N = L/\Delta x }[/math] so that [math]\displaystyle{ \Delta M = M/N = M(\Delta x/L) }[/math].
The Contribution of One Slice Approximation [math]\displaystyle{ r_\perp \approx x_n }[/math]: [math]\displaystyle{ \Delta I=(\Delta M)x^2 _n = (M/L)x^2 _n\Delta x. }[/math]
Adding Up the Contributions [math]\displaystyle{ I = \sum_{n=1}^N \Delta I = (M/L)\sum_{n=1}^N x^2 _n\Delta x }[/math].
The Finite Sum Becomes a Definite Integral [math]\displaystyle{ I = (M/L) \lim_{N \to \infty}\sum_{n=1}^N x^2 _n\Delta x }[/math] [math]\displaystyle{ = (M/L) \int\limits_{x_i}^{x_f}x^2\, dx }[/math].
The Limits of Integration Since the origin was at the center of the rod: [math]\displaystyle{ I = (M/L) \int\limits_{-L/2}^{+L/2}x^2\, dx = (1/12)ML^2 }[/math].
Hoop
The moment of inertia of a hoop or thin hollow cylinder of negligible thickness about its central axis is a straightforward extension of the moment of inertia of a point mass since all of the mass is at the same distance R from the central axis.[5]
Shpere
The moment of inertia of a sphere can be expressed as the summation of moments of infinitesimally thin disks about the z axis.

Cylinder
The moment of inertia of a solid cylinder can be calculated from the built up of moment of inertia of thin cylindrical shells. [7] Because only the perpendicular distances of atoms from the axis matter([math]\displaystyle{ r_\perp }[/math]), the moment of inertia for rotation about the axis of a long cylinder has exactly the same form as that of a disk. It means that the moment of inertia does not matter how long the cylinder is or how thick the disk is.
Other
The moments of inertia for different shapes can be calculated by applying integral calculus as shown in the calculation of moment of inertia for the Thin Rod or sphere.
Examples
1. The Moment of Inertia of a Diatomic Molecule What is the moment of inertia of a diatomic nitrogen molecule [math]\displaystyle{ N_2 }[/math] around its center of mass? The mass of a nitrogen atom is [math]\displaystyle{ 2.3 \times 10^{-26} kg }[/math] and the average distance between nuclei is [math]\displaystyle{ 1.5 \times 10^{-10} m. }[/math] Use the definition of moment of inertia carefully.
- Solution
- For two masses, [math]\displaystyle{ I = m_1r^2 {_\perp,_1} + m_2r^2 {_\perp,_2} }[/math]. The distance between masses is d, so the distance of each object from the center of mass is [math]\displaystyle{ r{_\perp,1} = r{_\perp,2} = (d/2) }[/math]. Therefore
- [math]\displaystyle{ I = M(d/2)^2 + M(d/2)^2 = 2M(d/2)^2 }[/math]
- [math]\displaystyle{ I = 2 \cdot (2.3 \times 10^{-26} kg)(0.75 \times 10^{-10} m)^2 }[/math]
- [math]\displaystyle{ I = 2.6 \times 10^{-46} kg \cdot m^2 }[/math]
- For two masses, [math]\displaystyle{ I = m_1r^2 {_\perp,_1} + m_2r^2 {_\perp,_2} }[/math]. The distance between masses is d, so the distance of each object from the center of mass is [math]\displaystyle{ r{_\perp,1} = r{_\perp,2} = (d/2) }[/math]. Therefore
- Solution
2. Calculate the moment of inertia of the array of point masses shown in figure 8-43 below. Assume m=1.8 kg and M=3.1 kg and the objects are wired together by very light, rigid pieces of wire. The array is rectangular with the dimensions indicated. The horizontal axis splits the 0.50 m distance in half. The vertical axis is 0.50 m from the left side of the rectangle. [8]
- Solution
- Part A: What is the moment of inertia about the vertical axis? [math]\displaystyle{ I = 1.8kg \times (0.50m)^2 + 1.8kg \times (1.50m)^2 + 3.1kg \times (0.50m)^2 + 3.1kg \times (1.50m)^2 = 12.25 kg\cdot m^2 }[/math]
- Part B: What is the moment of inertia about the horizontal axis? [math]\displaystyle{ I = 1.8kg \times (0.25m)^2 + 1.8kg \times (1.50m)^2 + 3.1kg \times (0.25m)^2 + 3.1kg \times (0.25m)^2 = 0.61 kg\cdot m^2 }[/math]
- Part C: About which axis would it be harder to accelerate this array? The one that has the largest moment of inertia is the hardest to accelerate and that is the vertical axis which has moment of inertia of 12.25 kg [math]\displaystyle{ \cdot m^2 }[/math]. Newton's 2nd Law in angular form is [math]\displaystyle{ \tau = I\alpha }[/math] so for a given torque [math]\displaystyle{ \tau }[/math], the object with the larger moment of inertia I has the smaller acceleration [math]\displaystyle{ \alpha }[/math] since [math]\displaystyle{ \alpha = \tau/I }[/math]
- Solution
See also
External links
http://www.bsharp.org/physics/spins
http://www.real-world-physics-problems.com/physics-of-figure-skating.html
References
- Nave, R. "Concepts" HyperPhysics. Web.
- Nave, R. "Moment of Inertia" HyperPhysics. Web.
- Urone, Paul Peter., Roger Hinrichs, Kim Dirks, and Manjula Sharma. "Rotational Inertia and Moment of Inertia." College Physics. Houston, TX: OpenStax College, Rice U, 2013. 354. Print.
- Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. Modern Mechanics. Hoboken, NJ: Wiley, 2011. Print.
- http://www.hunter.cuny.edu/physics/courses/physics110/repository/files/Giancoli_Prob.Solution%20Chap.8.pdf