Power (Mechanical)

Claimed by Aeze3

This topic covers Power.

The Main Idea

Power is the rate of doing work or the amount of energy consumed over an interval of time.

A Mathematical Model

When a force is applied over a distance in a unit of time, power is calculated by

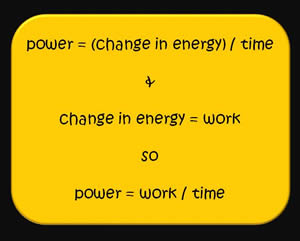
[math]\displaystyle{ power = \frac{F \Delta r}{\Delta t} = \frac{W}{\Delta t} }[/math]

where F is force, Δr is displacement, Δt is the duration of time and W is work.

It then follows that instantaneous power is

[math]\displaystyle{ power = F\cdot v }[/math]

where v is velocity.

The SI unit for power is watts (J/s)

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

A certain motor is capable of doing 3000 J of work in 12 s What is the power output of this motor?

[math]\displaystyle{ power = \frac{W}{\Delta t} = \frac{3000 J}{12 s} = 250 watts }[/math]

Middling

Here are questions dealing with human power. (a) If you follow a diet of 2000 food calories per day (2000 kC), what is your average rate of energy consumption in watts (power input)? (A food or “large” calorie is a unit of energy equal to 4.2 J; a regular or “small” calorie is equal to 4200 J.) (b) How many days of a diet of 2000 large calories are equivalent to the gravitational energy change from sea level to the top of Mount Everest, 8848 m above sea level? Assume your weight is 58 kg. (The body is not anywhere near 100% efficient in converting chemical energy into change in altitude. Also note that this is in addition to your basal metabolism.)

(a) [math]\displaystyle{ power = \frac{W}{\Delta t} = \frac{2000 kC}{day} \cdot \frac{4200 J}{1 kC} \cdot \frac{1 day}{24 h} \cdot \frac{1 h}{3600 s} = 97.2 watts }[/math]

(b) [math]\displaystyle{ {\frac{97.2 J}{s}} \cdot \frac{3600 s}{1 h} \cdot \frac{24 h}{1 day} = 8398080 J/day }[/math]

[math]\displaystyle{ \Delta U_g = mg\Delta y = (58 kg)(9.8 m/s^2)(8848 m - 0 m) = 5029203.2 J }[/math]

[math]\displaystyle{ \Delta t = \frac{W}{power} = \frac{5029203.2 J}{8398080 J/day} = 0.599 days }[/math]

Difficult

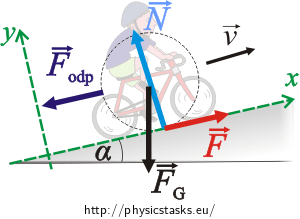
A bicyclist is going up an inclined slope with an angle [math]\displaystyle{ \alpha }[/math] = 2.9 degrees by a uniform speed of 27 km/h. The magnitude of the air resistance force is given by [math]\displaystyle{ F_{air} = kv^2 }[/math] kgs/m where the numerical value of [math]\displaystyle{ k = 0.3 }[/math] if the unit of the speed is m/s and the unit of the resistance force is the newton (N). The mass of the bicyclist including the bike is 70 kg. Do not consider the rolling resistance. (a) What forward force exerted on the bike by the road is needed to make the bicyclist move with constant speed? (b) How much work does the bicyclist do when riding a distance of 1200 m? (c) What is the power of the bicyclist during the ride? Assume there is no loss of mechanical energy.

[math]\displaystyle{ F_g }[/math] = weight

N = normal force exerted on the bike by the road

[math]\displaystyle{ F_{odp} }[/math] = air resistance

F = unknown forward force exerted on the bike by the road

(a) [math]\displaystyle{ x-components: -F_gsin\alpha -F_{odp} + F = 0 }[/math]

[math]\displaystyle{ y-components: N -F_gcos\alpha = 0 }[/math]

[math]\displaystyle{ F = F_gsin\alpha + F_{odp} = mgsin\alpha + kv^2 }[/math]

[math]\displaystyle{ v = \frac{27 km}{h} \cdot \frac{1000 m}{1 km} \cdot \frac{1 h}{3600 s} = 7.5 m/s }[/math]

[math]\displaystyle{ F = (70 kg)(9.8 m/s^2)sin2.9 + (0.3 kgs/m)(7.5 m/s)^2 = 51.6 N }[/math]

(b) [math]\displaystyle{ W = F\Delta r = (51.6 N)(1200 m) = 61920 J }[/math]

(c) [math]\displaystyle{ power = F\cdot v = (51.6 N)(7.5 m/s) = 387 watts }[/math]

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

Electrical power transmission has replaced mechanical power transmission in all but the very shortest distances. From the 16th century through the industrial revolution to the end of the 19th century mechanical power transmission was the norm. The oldest long-distance power transmission technology involved systems of push-rods connecting waterwheels to distant mine-drainage and brine-well pumps. The unit of power, the watt, was named after the engineer James Watt, for his contributions to the development of the steam engine.

See also

• Work
• Gravitational Potential Energy
• Newton's Second Law of Motion
• System & Surroundings

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

Chabay, Ruth W.; Sherwood, Bruce A. Matter and Interactions, 4th Edition: 1-2. Wiley.

"General Mechanics/Work and Power." - Wikibooks, Open Books for an Open World. Web. General Mechanics/Work and Power

<https://physicstasks.eu/280/bicyclist-going-uphill>.