RC Circuit

Work in progress by Joe Welch

The Main Idea

The figure below shows a capacitor, ( C ) in series with a resistor, ( R ) forming a RC Charging Circuit connected across a DC battery supply ( Vs ) via a mechanical switch. When the switch is closed, the capacitor will gradually charge up through the resistor until the voltage across it reaches the supply voltage of the battery. The manner in which the capacitor charges up is also shown below.

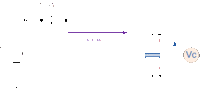
Let us assume left, that the capacitor, C is fully “discharged” and the switch (S) is fully open. These are the initial conditions of the circuit, then t = 0, i = 0 and q = 0. When the switch is closed the time begins at t = 0 and current begins to flow into the capacitor via the resistor.

Since the initial voltage across the capacitor is zero, ( Vc = 0 ) the capacitor appears to be a short circuit to the external circuit and the maximum current flows through the circuit restricted only by the resistor R.

As the capacitor charges up, the potential difference across its plates slowly increases with the actual time taken for the charge on the capacitor to reach its maximum possible voltage. The maximum voltage the capacitor reaches is equal to the voltage supply of the battery. Once the potential difference across the plates of the capacitor equals the battery's voltage supply, current will stop flowing through the circuit. This is known as the steady state of an RC circuit; it is reached when time goes to infinity.

A Mathematical Model

ΔV = I * R

Node Rule-Current is assigned (positive or negative) quantity reflecting direction towards or away from a node. this principle can be solved by adding all the currents up to equal 0.

alt text

Loop Rule-Similar to the node rule; however, the voltage jumps and drops are added up around the circuit to equal to 0./

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

In the steady state what is the potential difference across the plates of the capacitor?

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page