Gyroscopes

An explanation by Ansley Marks

A gyroscope is a device containing a wheel or disk that is free to rotate about its own axis independent of a change in direction of the axis itself. Since the spinning wheel persists in maintaining its plane of rotation, a gyroscopic effect can be observed.

The Main Idea

Although insignificant looking and seemingly uninteresting when still, gyroscopes become a fascinating device when in motion and can be explained using the angular momentum principle. Gyroscopes come in all different forms with varying parts. The main component of a gyroscope is a spinning wheel or a disk mounted on an axle. Typically gyroscopes contain a suspended rotor inside three rings called gimbals. In order to ensure that little torque is applied to the inside rotor, the gimbals are mounted on high quality bearing surfaces, allowing free movement of the spinning wheel in the middle. These types of gyroscopes with multiple gimbals are useful for stabilization because the wheels can change direction without affecting the inner rotor. If the spinning axle of a gyroscope is placed on a support, then a complex motion can be observed. The motion of a gyroscope will be modeled and explained further on in this page.

A Mathematical Model

When the spinning axis of a gyroscope is placed on a support, a gyroscopic effect is observed. The gyroscope bobs up and down--nutation--and rotates about the support--precession. For the sake of simplifying the mathematical equations for a gyroscope's motion, nutation (the upwards and downwards movement of the rotor) will be ignored. We will only look at the precession motion of the gyroscope.

A gyroscope processing in the x,z plane with the y-axis positioned upwards along the vertical support.

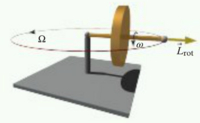
To start off with, the gyroscope's rotor rotates about its own axis with an angular velocity of ω and has a moment of inertia I. Thus, the rotational angular momentum of the rotor can be modeled as:

Lrot,r = Iω

Where the rotational angular momentum points horizontal to the rotor.

The Lrot,r will always change direction as the rotor rotates about the support. The rotor processes about the support with an angular velocity Ω, which is constant in magnitude and direction.

If Ω is known, then the velocity of the center of mass of the rotor device can be derived using the following relationship:

Ω = Vcm/r

Where r is equal to the distance from the support to the center of mass of the rotor device. The linear momentum of the gyroscope is then ΩP.

A view of the gyroscope from the side with all the forces labeled.

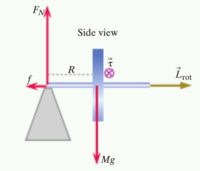
Since the rotor is processing about the support, there must be a perpendicular force f exerted by the support such that ΩP = f, where P is equal to M(Ωr). Thus, f = Mr[math]\displaystyle{ Ω^2 }[/math].

There is also a translational angular momentum of the rotor processing about the support. This can be modeled by finding the magnitude of the position vector crossed with the momentum.

Lsupport = |R x P |

Since the direction of the rotational angular momentum of the rotor around the support is constantly changing direction, the rate of change of the rotational angular momentum can be written as:

LrotΩ

Thus the only remaining element that is needed to complete the Angular Momentum Principle is the torque. The torque is equal to the distance from the support to the center of mass of the rotor, r, multiplied by the force exerted, which is the mass times gravity. Therefore, since the change in rotational angular momentum is LrotΩ, that must be equal to τCM. By setting the two equations equal to each other, the angular momentum can be isolated to one side. This yields the following result:

Ω = τCM/Lrot = rMg/Iω

Connectedness

This topic is interesting because gyroscopes have held the fascination of pretty much anyone that has ever seen one in motion including myself. Although the explanation that I gave was a simplified version of a gyroscope which only processes and doesn't nutate, there are many other complex mathematical models of the complicated motion of gyroscopes. Many papers and even books have been written on the subject of gyroscopes, and they have baffled nobel prize winners such as Niels Bohr and famous physicists alike. Gyroscopes are connected to my major because they are huge in industrial manufacturing of numerous materials. We use some sort of gyroscope in our everyday lives from cars to airplanes and other mechanical equipments.

History

Gyroscopes have been around for nearly 200 years. The first person to discover the gyroscope was Johann Bohnenberger in 1817 at the University of Tubingen. However, Bohnenberger was not credited with the discovery of the gyroscope. The French scientist Jean Bernard Leon Foucault (1826-1864) coined the term "gyroscope" and ended up with being credited for the discovery of a gyroscope. Thanks to his experiments with the gyroscope, they started to become mainstream and studied by many other physicists. In the early 20th century, gyroscopes were first used in boats and eventually in aircraft. Gyroscopes have been modified and tweaked to suit many purposes that are widely used today mainly as stabilizers.

See also

Further reading

Compass and Gyroscope: Integrating Science and Politics for the Environment

Mathematical model for gyroscope effects: http://scitation.aip.org/content/aip/proceeding/aipcp/10.1063/1.4915651

YouTube video on gyroscope procession: https://www.youtube.com/watch?v=ty9QSiVC2g0

Wikipedia: https://en.wikipedia.org/wiki/Gyroscope

External links

http://dictionary.reference.com/browse/precession

http://dictionary.reference.com/browse/nutation

https://en.wikipedia.org/wiki/Gyroscope

References

Oxford Dictionaries: http://www.oxforddictionaries.com/us/definition/american_english/gyroscope

HyperPhysics: http://hyperphysics.phy-astr.gsu.edu/hbase/gyr.html

Wikipedia: https://en.wikipedia.org/wiki/Gyroscope

Gyroscope History: http://www.gyroscopes.org/history.asp