Wavelength and Frequency
Under Construction By Allie Johnson
Wavelength and Frequency are used to describe a sinusoidal electromagnetic wave. Frequency is the number of peaks per second that pass a given location. Wavelength is the distance between two peaks.
The Main Idea
The frequency of a sinusoidal electromagnetic wave is also the inverse of the period. When that wave is plotted over time, a period will be the distance between two peaks. Frequency is measured in inverse seconds or hertz (Hz). Wavelength is the distance between two peaks of a sinusoidal electromagnetic wave when plotted over a direction.
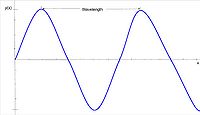
Wavelength is directly proportional to frequency. Wavelength is the speed of light divided by the frequency. Therefore, as frequency increases wavelength decreases. This is because over a specific amount of time, the wave will move at the speed of light. Electromagnetic radiation is categorized by its wavelength, spanning from gamma rays to radio waves.

A Mathematical Model
Relationship Between Frequency and Period
- [math]\displaystyle{ f = \frac{1}{T} }[/math] where F is the frequency and T is the period.
Relationship Between Frequency and Wavelength
- [math]\displaystyle{ f = \frac{c}{\lambda} }[/math] where F is the frequency, c is the speed of light constant (c = 2.998×108 m s−1), and lambda is the wavelength.
Relationship Between Frequency and Angular Frequency
- [math]\displaystyle{ \omega = {{2 \pi} \over T} = {2 \pi f} , }[/math] where ω is the angular frequency or angular speed (radians per second),T is the frequency over period (measured in seconds), and f is the ordinary frequency (measured in hertz).
A Computational Model

Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Problem #1a: Calculate the frequency of radiation with a wavelength of 442 nm. Example #1b: The wavelength of an argon laser's output is 488.0 nm. Calculate the frequency of this wavelength of electromagnetic radiation.
Solution to 1a:
1) Convert nm to m:
442 nm x (1 m / 109 nm) = 4.42 x 10¯7 m 2) Substitute into λν = c:
(4.42 x 10¯7 m) (x) = 3.00 x 108 m s¯1 x = 6.79 x 1014 s¯1
Solution to 1b:
1) Convert nm to m:
488 nm x (1 m / 109 nm) = 4.88 x 10¯7 m Then, substitute into λν = c:
(4.88 x 10¯7 m) (x) = 3.00 x 108 m s¯1 x = 6.15 x 1014 s¯1
The use of nm for wavelength is quite common.
Middling
Problem #2a: Calculate the frequency of electromagnetic radiation that has a wavelength of 1.315 micrometers. Problem #2b: What is the frequency of infrared radiation of wavelength 67.5 μm?
Solution to 2a:
1) Convert μm to m:
1.315 μm x (1 m / 106 μm) = 1.315 x 10¯6 m 2) Substitute into λν = c:
(1.315 x 10¯6 m) (x) = 3.00 x 108 m s¯1 x = 2.28 x 1014 s¯1
Solution to 2b:
1) Convert μm to m:
67.5 μm = 67.5 x 10-6 m 2) Use λν = c to determine the frequency:
(67.5 x 10-6 m) (x) = 3.00 x 108 m/s x = 4.44 x 1012 s-1
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
For more interest in the movement of sinusoidal waves over time visit: http://www.physicsbook.gatech.edu/Electromagnetic_Propagation
For interest in how wave length and frequency relate to radiation visit: http://www.physicsbook.gatech.edu/Sinusoidal_Electromagnetic_Radiaton
Further reading
Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. 3rd ed. Hoboken, NJ: Wiley, 2011. Print
External links
https://www.youtube.com/watch?v=tJW_a6JeXD8
References
This section contains the the references you used while writing this page