The Maxwell-Boltzmann Distribution

Claimed by Sai Srinivas

The Main Idea

In the context of the Kinetic Molecular Theory of Gases, a gas has a large number of particles moving around with varying speeds, colliding with each other, causing changes in the speeds and directions of the particles. A good understanding of the properties of a gas requires the knowledge of the distribution of particles speeds. Named after James Clerk Maxwell and Ludwig Boltzmann, the Maxwell-Boltzmann Distribution describes particles speeds in an idealized gas, in which the particles rarely interact with each other except for the brief collisions where energy and momentum are affected. The distribution of a particular gas depends on certain parameters, such as temperature of the system and mass of the gas particles. Certain properties of real gases inhibit their ability to be modeled by the Maxwell-Boltzmann Distribution so this distribution is best suited for application to ideal gases and certain rarefied gases at normal temperatures. Knowledge of particle speeds given by this distribution is important to scientists performing reactions because for a reaction to take place, particles must collide with sufficient energy to induce a transition state. This usually pertains to faster particles, so if the Maxwell-Boltzmann Distribution tells us how many particles have energies or speeds above a certain threshold, this is considered valuable information.

A Mathematical Model

The Maxwell–Boltzmann distribution is the function

[math]\displaystyle{ f(v) = \sqrt{\left(\frac{m}{2 \pi kT}\right)^3}\, 4\pi v^2 e^{- \frac{mv^2}{2kT}}, }[/math]

where [math]\displaystyle{ m }[/math] is the particle mass and [math]\displaystyle{ kT }[/math] is the product of Boltzmann's constant, [math]\displaystyle{ k }[/math], and thermodynamic temperature, given by [math]\displaystyle{ T }[/math].

The probability that a molecule of a gas has a center-of-mass speed within the range [math]\displaystyle{ v }[/math] to [math]\displaystyle{ v+dv }[/math] is given by [math]\displaystyle{ f(v)dv }[/math].

As has been mentioned, the Maxwell-Boltzmann Distribution details the distribution of particle speeds in an ideal gas, and this distribution can be characterized in a few ways shown below:

- The average speed, [math]\displaystyle{ v_{avg} }[/math], is the sum of the speeds of all particles divided by the number of particles in the volume of gas:

[math]\displaystyle{ v_{avg} = \int_0^{\infty} v \, f(v) \, dv= \sqrt { \frac{8kT}{\pi m}}= \sqrt { \frac{8RT}{\pi M}} }[/math]

where R is the gas constant and M is the molar mass of the substance.

- The most probable speed, [math]\displaystyle{ v_p }[/math], is the speed associated with the highest point on the Maxwell-Boltzmann Distribution curve. Only a few particles will have this speed. To find this point on the distribution, we must calculate df/dv, set it equal to zero, and then solve for v. Then, we can ascertain:

[math]\displaystyle{ v_p = \sqrt { \frac{2kT}{m} } = \sqrt { \frac{2RT}{M} } }[/math]

-The root-mean-square speed, [math]\displaystyle{ v_{rms} }[/math], is the square root of the average speed-squared and is given by:

[math]\displaystyle{ v_{rms} = \left(\int_0^{\infty} v^2 \, f(v) \, dv \right)^{1/2}= \sqrt { \frac{3kT}{m}}= \sqrt { \frac{3RT}{M} } }[/math]

If a gas is in thermal equilibrium and follows the Maxwell-Boltzmann Distribution, the following relation always is discovered:

[math]\displaystyle{ v_p \lt v_{avg} \lt v_{rms} }[/math]

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

To visualize how a Maxwell-Boltzmann Distribution plot looks like, the link below provides a demonstration to see how temperature of the system affects the particle speeds.

Maxwell-Boltzmann Temperature Effect Demo

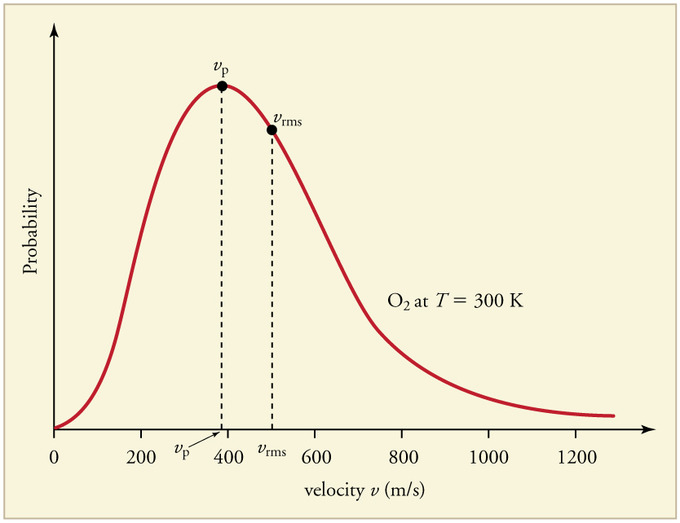
The graph below displays the Maxwell-Boltzmann Distribution of [math]\displaystyle{ O_2 }[/math] at 300 Kelvin. As one can see, the most probable speed, [math]\displaystyle{ v_p }[/math], is marked at the peak of the distribution curve. The root-mean-square speed, [math]\displaystyle{ v_{rms} }[/math], is also displayed on the curve.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Looking at the Maxwell-Boltzmann Distributions of several gases below, what can be said about the relationship between particle speed distributions and the mass of the particles?

It can be concluded that the heavier particles move slower on average and have a smaller range of particle speeds, whereas lighter particles are capable of faster speeds so they have much larger ranges of particle speeds.

Middling

Using the Maxwell-Boltzmann function, calculate the number of helium gas particles in a sample of 100,000 helium particles with a speed of 325 m/s at 500K. Given that [math]\displaystyle{ m_{helium} = 6.65 × 10^{-27} kg }[/math] and [math]\displaystyle{ k = 1.381 × 10^{-23} m^2*kg*s^{-2}*K^{-1} }[/math].

Given the Maxwell-Boltzmann function:

[math]\displaystyle{ f(v) = \sqrt{\left(\frac{m}{2 \pi kT}\right)^3}\, 4\pi v^2 e^{- \frac{mv^2}{2kT}}, }[/math]

We have been given the values of T, v, [math]\displaystyle{ m_{helium} }[/math], and [math]\displaystyle{ k }[/math]. From here, we can plug these values into the formula.

[math]\displaystyle{ f(325) = \sqrt{\left(\frac{(6.65 × 10^{-27})}{(2 \pi)(1.381 × 10^{-23})(500)}\right)^3}\, 4\pi (325)^2 e^{- \frac{(6.65 × 10^{-27})(325)^2}{2(1.381 × 10^{-23})(500)}}, }[/math]

[math]\displaystyle{ f(325) = .0000755 }[/math]

[math]\displaystyle{ Number of Helium Particles = f(325)*(100,000 Total) = 7.55 }[/math]

Based on this fraction, if there were 100,000 helium particles, there would only be between 7 or 8 particles with this speed at this temperature. This is a very small fraction of helium particles.

Difficult

Using the Maxwell-Boltzmann function, calculate the number of helium gas particles in a sample of 100,000 helium particles with a speed of 325 m/s at 500K. Given that [math]\displaystyle{ m_{helium} = 6.65 × 10^{-27} kg }[/math] and [math]\displaystyle{ k = 1.381 × 10^{-23} m^2*kg*s^{-2}*K^{-1} }[/math].

Given the Maxwell-Boltzmann function:

[math]\displaystyle{ f(v) = \sqrt{\left(\frac{m}{2 \pi kT}\right)^3}\, 4\pi v^2 e^{- \frac{mv^2}{2kT}}, }[/math]

We have been given the values of T, v, [math]\displaystyle{ m_{helium} }[/math], and [math]\displaystyle{ k }[/math]. From here, we can plug these values into the formula.

[math]\displaystyle{ f(325) = \sqrt{\left(\frac{(6.65 × 10^{-27})}{(2 \pi)(1.381 × 10^{-23})(500)}\right)^3}\, 4\pi (325)^2 e^{- \frac{(6.65 × 10^{-27})(325)^2}{2(1.381 × 10^{-23})(500)}}, }[/math]

[math]\displaystyle{ f(325) = .0000755 }[/math]

Number of Helium Particles [math]\displaystyle{ = f(325)*(100,000 Total) = 7.55 }[/math]

Based on this fraction, if there were 100,000 helium particles, there would only be between 7 or 8 particles with this speed at this temperature. This is a very small fraction of helium particles.

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

[1]

References

This section contains the the references you used while writing this page