Thermal Energy
Work in progress by KwangJun Jung
Thermal energy is energy possessed by an object or system due to the movement of particles within the object or the system.
The Main Idea
All objects are made up of numerous particles or molecules. Within these objects, those particles or molecules are constantly moving or vibrating, generating heat. Thermal energy refers to the internal energy that comes from these moving particles or molecules within the objects. What we mean by a change of "thermal" energy is that part of the internal energy that is associated with a temperature change. In many situations it isn't possible to say how much of the internal energy is thermal, but if the heat capacity is known, we can use a thermometer to measure a change in the thermal energy.
A Mathematical Model
Change in thermal energy can be calculated by using the following mathematical equation. [math]\displaystyle{ {Q = m*C*dT} }[/math] where [math]\displaystyle{ {Q} }[/math] is the thermal energy in Joules, [math]\displaystyle{ {m} }[/math] is the mass of an object in grams, [math]\displaystyle{ {C} }[/math] is the object's specific heat capacity, and [math]\displaystyle{ {dT} }[/math] is the change in object's temperature in Celsius.
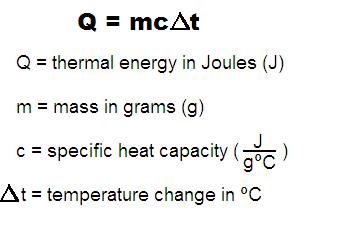
Examples
Simple
500g of water was heated from the initial temperature of 20°C to 50 °C. What is the change in thermal energy of water? (Heat capacity of water is 4.2J/g*°C)
1. List given things and equation
[math]\displaystyle{ Q = m*C*dT }[/math]
[math]\displaystyle{ Q=?, m=500g, C=4.2J/g*°C, dT={T}_{f}-{T}_{i}, {T}_{f}=50°C, {T}_{i}=20°C }[/math]
2. Plug the numbers into the equation and find the answer
[math]\displaystyle{ Q = 500g*4.2J/g*°C*(50°C-20°C) }[/math]
[math]\displaystyle{ Q = 63000J }[/math]
Middling
400g of water with initial temperature of 90°C (specific heat of 4.2 J/g*°C) are poured into an aluminum pan whose mass is 800g with initial temperature of 20°C (specific heat of 0.9 J/g*°C). After a short time, what is the temperature of the water?
1. Write the equation and list the knowns and unknowns
[math]\displaystyle{ {{dE}_{water}+{dE}_{pan} = 0}, dE = m*C*dT }[/math]
[math]\displaystyle{ {m}_{water} = 400g,{m}_{pan} = 800g, {C}_{water} = 4.2J/g*°C {C}_{Aluminum} = 0.9J/g*°C, {T}_{i water} = 90°C, {T}_{i pan} = 20°C, {T}_{f} = ? }[/math]
2. Plug the numbers into the equation
[math]\displaystyle{ 0 = 400g*4.2J/g*°C*({T}_{f}-90°C) + 800g*0.9J/g*°C*({T}_{f}-20°C) }[/math]
3. Solve for [math]\displaystyle{ {T}_{f} }[/math] and find its value
[math]\displaystyle{ {T}_{f}=69°C }[/math]
Difficult
500g of water with initial temperature of 87°C (specific heat of 4.2 J/g*°C) are poured into an aluminum pan whose mass is 800g with initial temperature of 22°C (specific heat of 0.9 J/g*°C). Then you place the pan on a hot electric stove. While the stove is heating the pan, you stir the water doing 26000J of work, rising temperature of a system to 82.5 °C. How much energy transfer due to a temperature difference was there from the stove into the system consisting of the water plus the pan?
1. Write the equation and find the final temperature when water and pan first reached thermal equilibrium.
[math]\displaystyle{ {{dE}_{water}+{dE}_{pan} = W + Q}, dE = m*C*dT }[/math]
[math]\displaystyle{ W=0, Q=0, {m}_{water}=500g, {m}_{pan}=800g, {C}_{water}=4.2 J/g*°C, {C}_{aluminum}=0.9 J/g*°C, {T}_{1water}=87°C, {T}_{1pan}=22°C, {T}_{2}=? }[/math]
2. Plug the numbers into the equation and find the final temperature
[math]\displaystyle{ {dE}_{water}= 500*4.2*({T}_{2}-87) }[/math]
[math]\displaystyle{ {dE}_{pan}=800*0.9*({T}_{2}-22) }[/math]
[math]\displaystyle{ {dE}_{water}+{dE}_{pan}=0 }[/math]
3. Solve for [math]\displaystyle{ {T}_{f} }[/math] and find its value
[math]\displaystyle{ {T}_{f} = 70.404 }[/math]
4. Write the equation and list the knowns, repeating the steps above (final temperature above now becomes initial temperature)
[math]\displaystyle{ {{dE}_{water}+{dE}_{pan} = W + Q}, dE = m*C*dT }[/math]
[math]\displaystyle{ W=26000J, Q=?, {m}_{water}=500g, {m}_{pan}=800g, {C}_{water}=4.2 J/g*°C, {C}_{aluminum}=0.9 J/g*°C,{T}_{2}=70.404°C, {T}_{3}=82.5°C }[/math]
5. Plug the numbers into the equation
[math]\displaystyle{ 500*4.2*(82.5-70.404)+800*0.9*(82.5-70.404) = 26000 + Q }[/math]
6. Solve for Q and find its value
[math]\displaystyle{ Q = 8110J }[/math]
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
I am a 1st year student in Mechanical Engineering. Under mechanical engineering there is a branch o physics called Thermodynamics which deals with heat and temperature and their relation to energy and work. Thermal Energy is one of the topic under Thermodynamics dealing with macroscopic variables especially internal energy.
- Is there an interesting industrial application?
History
Careful experiments show that the temperature increase of an object and its surroundings due to friction is directly related to the amount of mechanical energy lost. The most famous experimental demonstration of this fact was carried out by James Joule in the 1840’s. Joule hung some weights from pulleys so that as they fell, they turned a paddle-wheel apparatus immersed in a bucket of water. The friction between the paddles and the water raised the water’s temperature by an amount that was directly proportional to the distance that the weights fell. In our modern system of units, Joule found that raising the temperature of a kilogram of water by one degree Celsius required a loss in mechanical (gravitational) energy of approximately 4200 joules. Joule therefore proposed that this mechanical energy is not actually lost, but converted into a new type of energy: thermal energy, which manifests itself as an increase in temperature.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page
