Conservation of Momentum

Claimed by Shohini Ghosh- Choudhary (shohinigc)

Short Description of Topic

The Main Idea

The conservation of momentum is one of the fundamental laws of physics. Within the definitions of the problem, the total momentum of the system stays constant (1). Much like the conservation of mass or the conservation of energy, momentum is neither created nor destroyed. The momentum is changed through the action of forces (1) as in Newton’s law of motion. This is a powerful idea to solving problems. For example if a collision occurs 2 objects (object 1 and object 2) in an isolated system, the total momentum of the two objects before the collision is equal to the total momentum of the two objects after the collision (2). So, the momentum lost by object 1 is equal to the momentum gained by object 2 (2). The main difference between momentum conservation and conservation of mass or the conservation of energy is that momentum is a vector quantity, so momentum is conserved in the x, y and z directions at the same time (1).

The law of conservation of momentum can be logically derived from Newton’s Third Law (2). When 2 objects collide, the force on object 1 on object 2 ([math]\displaystyle{ \begin{align} F_1 \end{align} }[/math]) is equal in magnitude and opposite in direction to the force on object 2 on object 1 ([math]\displaystyle{ \begin{align} F_1 \end{align} }[/math]). So: [math]\displaystyle{ \begin{align} F_1=-F_2 \end{align} }[/math]

The objects collide during a certain time period ([math]\displaystyle{ \begin{align} \Delta t \end{align} }[/math]) so that the force acting on object 1 and the force acting on object 2 act over the this time period (Δt). So: [math]\displaystyle{ \begin{align} F_1* \Delta 1 =-F_2* \Delta 1 \end{align} }[/math] We know that [math]\displaystyle{ \begin{align} F*t \end{align} }[/math] is the formula for impulse and since the change in impulse is equal to the change in momentum: [math]\displaystyle{ \begin{align} m_1 * \Delta v_1 = -m_2 * \Delta v_2 \end{align} }[/math] (The Law of Conservation of Momentum).

A Mathematical Model

[math]\displaystyle{ \begin{align} \Delta p_1 = m_1 * \Delta v_1 = -m_2 * \Delta v_2 = \Delta p_2 \,. \end{align} }[/math]

[math]\displaystyle{ \begin{align} p_1 \end{align} }[/math] is the momentum of the first object, [math]\displaystyle{ \begin{align} m_1 \end{align} }[/math] is the mass of the first object, [math]\displaystyle{ \begin{align} v_1 \end{align} }[/math] is the velocity of the first object. [math]\displaystyle{ \begin{align} p_2 \end{align} }[/math] is the momentum of the second object, [math]\displaystyle{ \begin{align} m_2 \end{align} }[/math] is the mass of the second object, [math]\displaystyle{ \begin{align} v_2 \end{align} }[/math] is the velocity of the second object.

A Computational Model

The link below shows a simulation of an elastic collision where one object transfers all of its momentum to the second object after the collision.

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

[<iframe src="https://trinket.io/embed/glowscript/7bc4cb8e9a" width="100%" height="356" frameborder="0" marginwidth="0" marginheight="0" allowfullscreen></iframe>]

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

You are playing pool with your friends at Tech Rec. Two cue balls collide in a head-on collision. Both cue balls have equal mass of 0.165 kg. Before the collision the first ball is travelling at 9.8 meters per second and the second ball is stationary. After the collision the first ball travels at velocity 2 meters per second. What is the velocity of the second ball?

Solution: [math]\displaystyle{ \begin{align} m_1 = m_2 = m = 0.165 \,. \end{align} }[/math]

[math]\displaystyle{ \begin{align} v_1i = 9.8 \,. \end{align} }[/math]

[math]\displaystyle{ \begin{align} v_1f = -2 \,. \end{align} }[/math]

[math]\displaystyle{ \begin{align} V_2i = 0 \,. \end{align} }[/math]

[math]\displaystyle{ \begin{align} m * (v_1f - v_1i)= m (v_2f - v_2i) \,. \end{align} }[/math]

[math]\displaystyle{ \begin{align} v_2f = v_1f - v_1i + v_2i = 9.8 + 2 - 0 = 11.8 \,. \end{align} }[/math] The velocity of the second ball is 11.8 meters per second in the positive x direction.

Middling

You looking out the window of your dorm when you see a person a Hoverboard collide with a person on a bike. The person on bike was going west with velocity 9 m/s and the person on the Hoverboard was traveling at 30 degrees north of west with velocity 5 m/s. After collision both the person on the Hoverboard and the person on the bike become entangled and travel together at some velocity [math]\displaystyle{ \begin{align} v_f \, \end{align} }[/math]. Find [math]\displaystyle{ \begin{align} v_f \, \end{align} }[/math] (See Figure 1 Below)

Figure 1

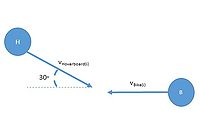
Solution: [math]\displaystyle{ \begin{align} v_H=[9*cos(30), 9*sin(30), 0] \, \end{align} }[/math] [math]\displaystyle{ \begin{align} v_B=[-5,0,0] \, \end{align} }[/math]

[math]\displaystyle{ \begin{align} m_H = 60 kg \, \end{align} }[/math] [math]\displaystyle{ \begin{align} m_B = 50 kg \, \end{align} }[/math]

[math]\displaystyle{ \begin{align} m_H*v_H + m_bike*v_B = (m_H+m_B)*v_final \, \end{align} }[/math]

[math]\displaystyle{ \begin{align} v_f= (m_H*v_H + m_B*v_B)/ (m_H+m_B) \, \end{align} }[/math]

[math]\displaystyle{ \begin{align} v_f = [-1.5155, -4.8503, 0] \,. \end{align} }[/math] m/s

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

[1]

References

1. "Conservation of Momentum." Conservation of Momentum. NASA, 05 May 2015. Web. 05 Dec. 2015. 2. "Momentum Conservation Principle." Momentum Conservation Principle. The Physics Classroom, n.d. Web. 05 Dec. 2015. <http://www.physicsclassroom.com/class/momentum/Lesson-2/Momentum-Conservation-Principle>.