Conservation of Momentum
Claimed by Shohini Ghosh- Choudhary (shohinigc)
The conservation of momentum is one of the fundamental laws of physics. Within the definitions of the problem, the total momentum of the system stays constant (1). Much like the conservation of mass or the conservation of energy, momentum is neither created nor destroyed. The momentum is changed through the action of forces (1) as in Newton’s law of motion. This is a powerful idea to solving problems.
The Main Idea
In a system, the total momentum must be conserved. For example, if a collision occurs 2 objects (object 1 and object 2) in an isolated system, the total momentum of the two objects before the collision is equal to the total momentum of the two objects after the collision (2). So, the momentum lost by object 1 is equal to the momentum gained by object 2 (2). The main difference between momentum conservation and conservation of mass or the conservation of energy is that momentum is a vector quantity, so momentum is conserved in the x, y and z directions at the same time (1).
The law of conservation of momentum can be logically derived from Newton’s Third Law (2). When 2 objects collide, the force on object 1 on object 2 ([math]\displaystyle{ \begin{align} F_1 \end{align} }[/math]) is equal in magnitude and opposite in direction to the force on object 2 on object 1 ([math]\displaystyle{ \begin{align} F_1 \end{align} }[/math]). So: [math]\displaystyle{ \begin{align} F_1=-F_2 \end{align} }[/math]
The objects collide during a certain time period ([math]\displaystyle{ \begin{align} \Delta t \end{align} }[/math]) so that the force acting on object 1 and the force acting on object 2 act over the this time period (Δt). So: [math]\displaystyle{ \begin{align} F_1* \Delta 1 =-F_2* \Delta 1 \end{align} }[/math] We know that [math]\displaystyle{ \begin{align} F*t \end{align} }[/math] is the formula for impulse and since the change in impulse is equal to the change in momentum: [math]\displaystyle{ \begin{align} m_1 * \Delta v_1 = -m_2 * \Delta v_2 \end{align} }[/math] (The Law of Conservation of Momentum).
A Mathematical Model
[math]\displaystyle{ \begin{align} \Delta p_1 = m_1 * \Delta v_1 = -m_2 * \Delta v_2 = \Delta p_2 \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} p_1 \end{align} }[/math] is the momentum of the first object, [math]\displaystyle{ \begin{align} m_1 \end{align} }[/math] is the mass of the first object, [math]\displaystyle{ \begin{align} v_1 \end{align} }[/math] is the velocity of the first object. [math]\displaystyle{ \begin{align} p_2 \end{align} }[/math] is the momentum of the second object, [math]\displaystyle{ \begin{align} m_2 \end{align} }[/math] is the mass of the second object, [math]\displaystyle{ \begin{align} v_2 \end{align} }[/math] is the velocity of the second object.
A Computational Model
The link below shows a simulation of an elastic collision where one object transfers all of its momentum to the second object after the collision.
Examples
Simple
You are playing pool with your friends at Tech Rec. Two cue balls collide in a head-on collision. Both cue balls have equal mass of 0.165 kg. Before the collision the first ball is travelling at 9.8 meters per second and the second ball is stationary. After the collision the first ball travels at velocity 2 meters per second. What is the velocity of the second ball?
Solution: [math]\displaystyle{ \begin{align} m_1 = m_2 = m = 0.165 \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_1i = 9.8 \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_1f = -2 \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} V_2i = 0 \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} m * (v_1f - v_1i)= m (v_2f - v_2i) \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_2f = v_1f - v_1i + v_2i = 9.8 + 2 - 0 = 11.8 \,. \end{align} }[/math] The velocity of the second ball is 11.8 meters per second in the positive x direction.
Middling
You looking out the window of your dorm when you see a person a Hoverboard collide with a person on a bike. The person on bike was going west with velocity 9 m/s and the person on the Hoverboard was traveling at 30 degrees north of west with velocity 5 m/s. After collision both the person on the Hoverboard and the person on the bike become entangled and travel together at some velocity [math]\displaystyle{ \begin{align} v_f \, \end{align} }[/math]. Find [math]\displaystyle{ \begin{align} v_f \, \end{align} }[/math] (See Figure 1 Below)
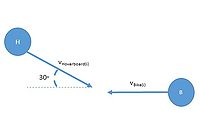
Solution: [math]\displaystyle{ \begin{align} v_H=[9*cos(30), 9*sin(30), 0] \, \end{align} }[/math] [math]\displaystyle{ \begin{align} v_B=[-5,0,0] \, \end{align} }[/math]
[math]\displaystyle{ \begin{align} m_H = 60 kg \, \end{align} }[/math] [math]\displaystyle{ \begin{align} m_B = 50 kg \, \end{align} }[/math]
[math]\displaystyle{ \begin{align} m_H*v_H + m_bike*v_B = (m_H+m_B)*v_final \, \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_f= (m_H*v_H + m_B*v_B)/ (m_H+m_B) \, \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_f = [-1.5155, -4.8503, 0] \,. \end{align} }[/math] m/s
Difficult
During a baseball game the 0.145 kg baseball is thrown straight upward with a velocity of 40 m/s. What is the recoil velocity of the earth? Why don’t we notice that the earth has gained velocity?
Solution: [math]\displaystyle{ \begin{align} m_b = 0.145 kg \, \end{align} }[/math] [math]\displaystyle{ \begin{align} m_E = 5.972 e 24 kg\, \end{align} }[/math] [math]\displaystyle{ \begin{align} v_b = 40 m/s \, \end{align} }[/math]
The system is the baseball and the earth. So the total momentum of the system must be conserved.
[math]\displaystyle{ \begin{align} m_b*v_b=-m_E*v_E .\, \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_e= - (m_b*v_b)/m_E .\, \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_e=- 9.7120e-25 m/s .\, \end{align} }[/math]
Even though the magnitude of the momentum of the ball equals the magnitude of the momentum of the Earth, the Earth’s mass is so massive that the Earth recoils with a velocity so small we don’t feel it.
Connectedness
The Conservation of Momentum is especially important in fluid flow and transport. As a Biomedical Engineer, I'm often times working with fluids flowing through the body. So when a new design for a pacemaker is made I would need to find out how the new pacemaker diverts fluid flow in the body. To solve a problem like this I would use Reynold's Transport Theorem, but the basis for Reynold's Transport Theorem is Conservation of Mass and Conservation of Momentum. No new device is be made for the human body without such an analysis. In addition, in certain disease states such as atherosclerosis when certain arteries become clogged, the fluid flow is diverted and there is a change in pressure. To model certain situations I would start from basic principles such as Conservation of Mass and Conservation of Momentum.
In this way, the Conservation Laws play important roles in most engineering majors. To name a few examples, Chemical Engineers are concerned with fluid flowing through a pipe, and Mechanical Engineers are concerned with fluid flowing through an engine.
History
Newton established the Conservation of Momentum along with the other Conservation Laws (except Conservation of Energy). Newton published his theories in 1687 in Philosophiæ Naturalis Principia Mathematica (linked below in external links). When Newton was publishing his work, the challenge that he faced was describing his theories without using calculus. Newton did not publish his La Methode Dex Fluxions until 1736. Newton's work on momentum was mostly focused on forces rather than energy and vectors.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
For extra concept quetions see: [2]
External links
References
1. "Conservation of Momentum." Conservation of Momentum. NASA, 05 May 2015. Web. 05 Dec. 2015.
2. "Momentum Conservation Principle." Momentum Conservation Principle. The Physics Classroom, n.d. Web. 05 Dec. 2015. <http://www.physicsclassroom.com/class/momentum/Lesson-2/Momentum-Conservation-Principle>.